Свободные, скользящие и фиксированные векторы
Иногда вместо того, чтобы рассматривать в качестве векторов множество всех равных направленных отрезков, берут только некоторую модификацию этого множества (фактормножество). Так, говорят о «свободных» (когда отождествляются все равные по длине и направлению направленные отрезки, считаясь полностью равными или — одним и тем же вектором), «скользящих» (отождествляются между собой все направленные отрезки, равные в смысле свободных векторов, начала и концы которых расположены на одной прямой) и «фиксированных» векторах (по сути дела, просто о направленных отрезках, когда разное начало означает уже неравенство векторов).
Иными словами, подразумевается, что свободный вектор может быть перенесен (параллельным переносом) как угодно (так, чтобы его начало совпало с любой точкой пространства), однако не перестает от этого быть собой. Скользящий же вектор может так же свободно переноситься только вдоль прямой, на которой он лежит, а фиксированный вообще не может переноситься. То есть его приложение к другой точке не имеет смысла; в частности любые операции, такие как сложение или вычитание, фиксированного вектора с фиксированным вектором, имеющим другое начало («приложенным к другой точке») не определены (не имеют смысла).
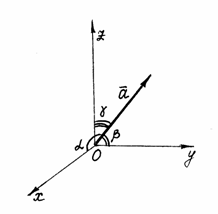
Направляющие косинусы вектора |
Направление
вектора в пространстве определяется
углами
Рис. 12
Из
свойств проекций:
Легко показать, что
1)
2) координаты
любого единичного вектора совпадают
с его направляющими косинусами: |
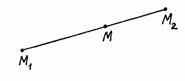
§ 6. Деление отрезка в данном отношении |
Говорят,
что точка
Рис. 13
Пусть
координаты точек
В
частности, если
–
середина отрезка
,
то
Пример
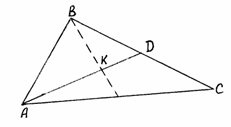
4. Даны
вершины треугольника
Решение. AD –
медиана, следовательно, D –
середина
отрезка BC,
ее координаты находятся по формулам
(2.7):
Рис. 14
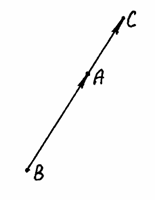
Пример
5. Показать,
что точки
Решение.
Рассмотрим векторы
|
,
которые вектор образует с осями
координат (рис. 12). Косинусы этих углов
называютсянаправляющими
косинусами вектора: 
, 
, 
.
, 
, 
.
Следовательно,
, 
, 
. (2.5)
;
.
делит
отрезок 
в
отношении 
,
если 
,
или 
(рис.
13).
и 
известны: 
, 
.
Найдем координаты точки 
.
Очевидно, что 
,
где 
, 
.
Приравнивая координаты векторов,
найдем:
, 
, 
. (2.6)
,
тогда
, 
, 
. (2.7)
, 
, 
.
Найти точку пересечения медиан этого
треугольника и орт вектора 
(рис.
14).
, 
, 
,
то есть 
.
Медианы точкой пересечения K делятся
в отношении 2:1, значит, 
,
тогда по формулам (2.6) найдем координаты
точки K: 
, 
, 
.
Таким образом, точка пересечения
медиан – 
.
Найдем координаты вектора
по
формуле (2.3) и его длину по формуле
(2.2): 
; 
.
Координаты единичного вектора совпадают
с его направляющими косинусами. По
формулам (2.5) 
, 
, 
,
следовательно, 
–
орт вектора
.
, 
, 
лежат
на одной прямой, причем A –
между B и C.
и 
(рис.
15). Если точки A,
B, C лежат
на одной прямой, то векторы
и
должны
быть кол-линеарны (условие 2.4). А если
точка A лежит
между B и C,
то
и
должны
быть сонаправлены (коэффициент
пропорциональности координат 
)
и 
.
Проверим выполнение этих условий.
, 
; 
,
следовательно,
.
Координаты вектора
больше,
значит, он длиннее и точка A лежит
между B и C.
ВЕКТОРЫ. ДЕЙСТВИЯ НАД ВЕКТОРАМИ. СКАЛЯРНОЕ,
ВЕКТОРНОЕ, СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.