1. Прямоугольная система координат в пространстве
Прямоугольная (или декартова) система координат в пространстве задается тройкой попарно перпендикулярных координатных осей, имеющих общее начало в точке О и одинаковый масштаб.
Оси координат в пространстве обычно обозначают Ох, Оу, Оz (оси абсцисс, ординат и аппликат соответственно).
В пространстве возможны правые (рис.)
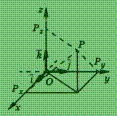
и левые (рис.)
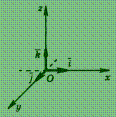
системы координат;
мы будем использовать правую
систему координат.
Орты
осей Ох, Оу, Оz —
это единичные векторы 
с
началом в точке О;
направления ортов совпадают с направлением осей.
Орты правой системы координат образуют правую тройку векторов.
Координатные плоскости хОу, уОz, хОz делят пространство на восемь октантов.
Координаты х, у, z точки Р в
пространстве определяются аналогично
координатам на плоскости:
это
координаты (на соответствующих осях)
оснований 
перпендикуляров,
опущенных из точки Р на
оси Ох, Оу, Оz ,
— соответственно абсцисса, ордината
и аппликата.
Координаты
обычно указывают в скобках: Р(х; у; z).
Между
точками в пространстве и тройками их
координат имеется взаимно
однозначное соответствие.
Расстояние
между двумя точками 
и 
в
пространстве определяется с помощью
теоремы Пифагора: 
В
частности, расстояние любой точки Р(х; у; z)
до начала координат равно 
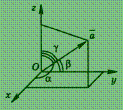
Координатами 
вектора 
в
прямоугольной системе координат Охуz в
пространстве называются его проекции
на координатные оси Ох, Оу, Оz: 
.
Здесь α , β , γ — углы между вектором и
соответствующимиположительными
полуосями (рис.).
Вектор с координатами записывают в виде
или 
.
При
сложении векторов их соответствующие
координаты складываются, при умножении
вектора на число — умножаются на
это число: 
.
Модуль вектора
вычисляется
по формуле 
В случае векторов
на плоскости хОу справедливы
те же формулы, но отсутствует третья
координата; например, 
Координаты
вектора 
,
заданного двумя точками
и 
равны разностям
соответствующих координат точек А и В: 
,
т. е. чтобы найти координаты некоторого
вектора, достаточно из координат его
конца вычесть одноименные координаты
его начала.
Любой вектор
на
плоскости может быть разложен
по ортам 
прямоугольной
системы координат хОу: 
.
Разложение по ортам 
в
пространстве имеет вид 
.
Векторные
слагаемые 
называются составляющими (или компонентами)
вектора
по
осям Ох, Оу, Оz.
Условие
коллинеарности двух векторов.
Два
ненулевых вектора
и
коллинеарны тогда
и только тогда, когда их одноименные
координаты пропорциональны, т. е. 
(1)
В равенстве (1) некоторые из знаменателей
могут оказаться равными нулю.
Условимся всякую
пропорцию 
понимать
в смысле равенства 
.
Например,
равенства
означают,
что
,
т. е. что 
.
В случае векторов
на плоскости условие (1) принимает
вид 
(2)
Пусть даны
точки 
и 
.
Требуется найти точку М(х; у; z),
лежащую на отрезке 
и
делящую его в данном отношении: 
Очевидно, что
или
Деление отрезка в заданном отношении. Координаты середины отрезка. Определение площади треугольника по известным координатам его вершин. Площадь многоугольника
1. Если x1 и y1 -
координаты точки A,
а x2 и y2 -
координаты точки B,
то координаты xи y точки C,
делящей отрезок AB в
отношении 
,
определяются по формулам
Если 
,
то точка C(x, y)
делит отрезок AB пополам,
и тогда координаты x и yсередины
отрезка AB определяются
по формулам
2. Площадь треугольника по известным координатам его вершин A(x1, y1), B(x2, y2),C(x3, y3) вычисляется по формуле
Полученное с помощью этой формулы число следует взять по абсолютной величине.
3. Площадь многоугольника с вершинами A(x1, y1), B(x2, y2), C(x3, y3), ..., F(xn, yn) равна
Выражение
вида 
равно x1y2 - x2y1 и
называется определителем второго
порядка.
Расстояние между двумя точками на плоскости
|
Расстояние между двумя данными точками равно корню квадратному из суммы квадратов разностей одноименных координат этих точек.
Пример 1. Найти расстояние между точками (-1;4) и (2;0). Решение: Искомое расстояние вычисляется по формуле (1). Здесь x1=-1, y1=4, x2=2, y2=0. Следовательно, |
2.