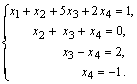- •Как вычислить определитель?
- •Свойства определителей
- •Описание метода
- •Понятие матрицы
- •Как найти обратную матрицу?
- •Решение системы линейных уравнений матричным методом
- •Решение произвольных систем линейных уравнений
- •Метод последовательного исключения неизвестных (метод Гаусса)
- •Переход к другому базису
- •Нахождение опорных решений
- •1. Прямоугольная система координат в пространстве
- •Деление отрезка в заданном отношении. Координаты середины отрезка. Определение площади треугольника по известным координатам его вершин. Площадь многоугольника
- •Свободные, скользящие и фиксированные векторы
- •1. Векторы, действия над векторами.
- •1) Сложение векторов.
- •2) Вычитание векторов.
- •3) Умножение вектора на число.
- •2. Координаты вектора
- •3. Базис системы векторов.
- •Пример.
- •Скалярное произведение векторов
- •Векторное произведение векторов
- •Смешанное произведение векторов
- •Геометрический смысл смешанного произведения
- •Свойства смешанного произведения:
- •Теорема 6. Всякая элементарная функция непрерывна в каждой точке, в которой она определена. Первый замечательный предел
- •Модификации первого замечательного предела
- •Второй замечательный предел
- •*3) Бесконечно малые величины
- •*4) Непрерывные функции Определения
- •Типы разрывов
- •5)Производная, правила и формулы дифференцирования
- •6)Правила дифференцирования
- •11Уравнение касательной и нормали
- •12. Производные высших порядков
- •13. Дифференциалы высших порядков и их неинвариантность
- •Основные дифференциалы
- •14. Теоремы Ролля, Лагранжа, Коши
- •15.Ряды Тейлора,Маклорена
- •16. Правило Лопиталя
- •17. Возрастание и убывание функции на интервале, экстремумы.
- •Необходимые определения.
- •Достаточные признаки возрастания и убывания функции.
- •Достаточные признаки экстремума функции.
- •18. Выпуклость, вогнутость и точки перегиба функции
- •19.Асимптоты
- •2. Нахождение асимптоты
- •2.1 Геометрический смысл асимптоты
- •2.2 Общий метод отыскания асимптоты
- •3.1 Горизонтальная асимптота
- •3.2 Вертикальная асимптота(рис.4)
- •3.3 Наклонная асимптота
- •20. Построение графика квадратичной функции по направлению ветвей, характерным точкам и оси симметрии параболы Примеры:
Переход к другому базису
Перейти от одного базиса системы к другому позволяет преобразование однократного замещения: вместо одной из основных переменных в базис вводят одну из свободных переменных. Для этого в столбце свободной переменной выбирают ключевой элемент и выполняют преобразования по указанному выше алгоритму, начиная с п. 2.
Нахождение опорных решений
Опорным решением системы линейных уравнений называется базисное решение, не содержащее отрицательных компонент.
Опорные решения системы находят методом Гаусса при выполнении следующих условий.
1. В
исходной системе все свободные члены
должны быть неотрицательны: ![]() .
.
2. В число базисных может быть введена только та переменная, в столбце коэффициентов при которой есть хотя бы один положительный элемент.
3. Если при переменной, вводимой в базис, имеются положительные коэффициенты в нескольких уравнениях, то переменная вводится в базис в то уравнение, которому соответствует наименьшее в столбце отношение свободных членов к этим положительным коэффициентам.
Замечание
1. Если
в процессе исключения неизвестных
появится уравнение, в котором все
коэффициенты неположительны,
а свободный член ![]() ,
то система не имеет неотрицательных
решений.
,
то система не имеет неотрицательных
решений.
Замечание 2. Если в столбцах коэффициентов при свободных переменных нет ни одного положительного элемента, то переход к новому опорному решению невозможен.
12.
Метод Гаусса решения систем линейных уравнений |
Формулы Крамера и матричный метод решения систем линейных уравнений не имеют серьезного практического применения, так как связаны с громоздкими выкладками. Практически для решения систем линейных уравнений чаще всего применяется метод Гаусса, состоящий в последовательном исключении неизвестных по следующей схеме.Для того чтобы решить систему уравнений
Рассмотрим метод Гаусса на примерах. Пример 14. Установить совместность и решить систему
Решение. Выпишем
расширенную матрицу системы и поменяем
местами первую и вторую строки для
того, чтобы элемент
Имеем
Выпишем
систему уравнений, расширенную матрицу
которой мы получили в результате
преобразований:
Итак,
имеем |
Векторная алгебра

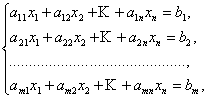 выписывают
расширенную матрицу этой системы
выписывают
расширенную матрицу этой системы 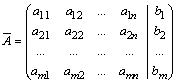 и
над строками этой матрицы производят
элементарные преобразования, приводя
ее к виду, когда ниже главной диагонали,
содержащей элементы
и
над строками этой матрицы производят
элементарные преобразования, приводя
ее к виду, когда ниже главной диагонали,
содержащей элементы 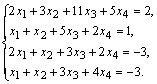
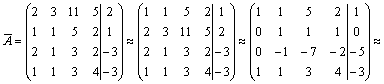
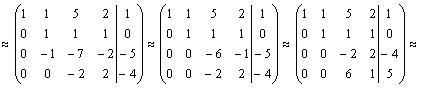
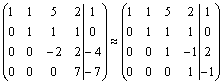 .
.