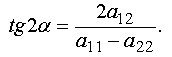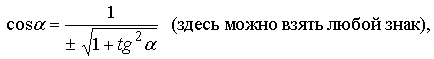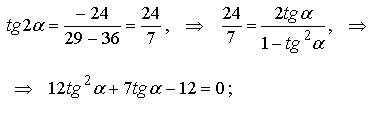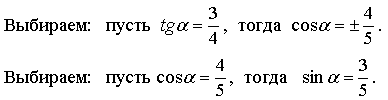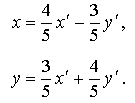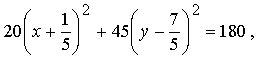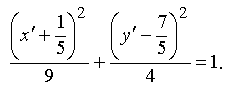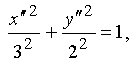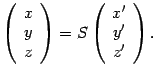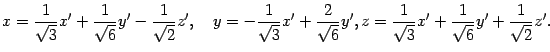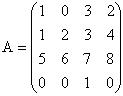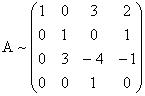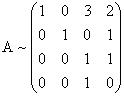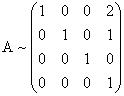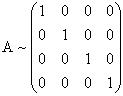- •Как вычислить определитель?
- •Свойства определителей
- •Описание метода
- •Понятие матрицы
- •Как найти обратную матрицу?
- •Решение системы линейных уравнений матричным методом
- •Решение произвольных систем линейных уравнений
- •Метод последовательного исключения неизвестных (метод Гаусса)
- •Переход к другому базису
- •Нахождение опорных решений
- •1. Прямоугольная система координат в пространстве
- •Деление отрезка в заданном отношении. Координаты середины отрезка. Определение площади треугольника по известным координатам его вершин. Площадь многоугольника
- •Свободные, скользящие и фиксированные векторы
- •1. Векторы, действия над векторами.
- •1) Сложение векторов.
- •2) Вычитание векторов.
- •3) Умножение вектора на число.
- •2. Координаты вектора
- •3. Базис системы векторов.
- •Пример.
- •Скалярное произведение векторов
- •Векторное произведение векторов
- •Смешанное произведение векторов
- •Геометрический смысл смешанного произведения
- •Свойства смешанного произведения:
- •Теорема 6. Всякая элементарная функция непрерывна в каждой точке, в которой она определена. Первый замечательный предел
- •Модификации первого замечательного предела
- •Второй замечательный предел
- •*3) Бесконечно малые величины
- •*4) Непрерывные функции Определения
- •Типы разрывов
- •5)Производная, правила и формулы дифференцирования
- •6)Правила дифференцирования
- •11Уравнение касательной и нормали
- •12. Производные высших порядков
- •13. Дифференциалы высших порядков и их неинвариантность
- •Основные дифференциалы
- •14. Теоремы Ролля, Лагранжа, Коши
- •15.Ряды Тейлора,Маклорена
- •16. Правило Лопиталя
- •17. Возрастание и убывание функции на интервале, экстремумы.
- •Необходимые определения.
- •Достаточные признаки возрастания и убывания функции.
- •Достаточные признаки экстремума функции.
- •18. Выпуклость, вогнутость и точки перегиба функции
- •19.Асимптоты
- •2. Нахождение асимптоты
- •2.1 Геометрический смысл асимптоты
- •2.2 Общий метод отыскания асимптоты
- •3.1 Горизонтальная асимптота
- •3.2 Вертикальная асимптота(рис.4)
- •3.3 Наклонная асимптота
- •20. Построение графика квадратичной функции по направлению ветвей, характерным точкам и оси симметрии параболы Примеры:
Решение системы линейных уравнений матричным методом
Еще один, пользующийся большой популярностью метод. Этот способ или, как его еще называеют, метод обратной матрицы называется так потому, что все решение сводится к простому матричному уравнению, для решения которого необходимо найти обратную матрицу. Для того, что бы расставить все точки над и, рассмотрим метод под микроскопом.
Алгоритм решения достаточно просто. Как и в методах Гаусса и Крамера первоначально надо проверить, имеет ли система уравнений решение по теореме Кронекера-Копелли. Затем для решения матричным методом необходимо ввести в рассмотрение матрицы-столбцы для неизвестных X и свободных членов B. Тогда систему линейных уравнений можно записать в матричной форме AX=B. Умножив это матричное уравнение на A-1, получим A-1AX= A-1B, откуда EX=X=A-1B. Следовательно, матрица-решение X легко находится как произведение A-1 и B.
Для большей ясности решим небольшой пример методом обратной матрицы:
21x1-45x2-3.5x3=10
12x1-16x2+21x3=-16
14x1+13x2-8x3=10
Определим совместность системы уравнений. По теореме Кронекера-Копелли для того, что бы система линейных алгебраических уравнений была совместна (имела решение), необходимо и достаточно, что быранг основной матрицы
A= |
|
и ранг расширенной матрицы
B= |
|
были равны. Так как rang|A|=3 равен rang|B|=3 и равен количеству неизвестных n=3, то система имеет единственное решение.
Для решения методом обратной матрицы необходимо ввести матричные обозначения
A= |
|
X= |
|
C= |
|
, то X=A-1C |
Найдем обратную матрицу A-1. Как ее найти, показывать не будем. Воспользовавшись нашии онлайн калькулятором, вы сможете выбрать один из двух способов для ее нахождения. Она будет иметь вид.
A-1= |
|
Для нахождения матрицы X умножим обратную матрицу А-1 на матрицу С
|
|
= |
|
Получили решение системы уравнений X1=0.227 X2=-0.209 X3=-1.194
8.
Собственными
числами матрицы ![]() являются
корни уравнения
являются
корни уравнения
![]()
и только они.
Доказательство.
Пусть столбец ![]() --
собственный вектор матрицы
с
собственным числом
--
собственный вектор матрицы
с
собственным числом ![]() .
Тогда, по определению,
.
Тогда, по определению, ![]() .
Это равенство можно переписать в виде
.
Это равенство можно переписать в виде ![]() .
Так как для единичной матрицы
.
Так как для единичной матрицы ![]() выполнено
выполнено ![]() ,
то
,
то ![]() .
По свойству матричного умножения
.
По свойству матричного умножения ![]() и
предыдущее равенство принимает вид
и
предыдущее равенство принимает вид
|
(19.4) |
Допустим,
что определитель матрицы ![]() отличен
от нуля,
отличен
от нуля, ![]() .
Тогда у этой матрицы существует
обратная
.
Тогда у этой матрицы существует
обратная ![]() .
Из равенства (19.4)
получим, что
.
Из равенства (19.4)
получим, что ![]() ,
что противоречит определению собственного
вектора. Значит, предположение, что
,
неверно, то есть все собственные числа
должны являться корнями уравнения
.
,
что противоречит определению собственного
вектора. Значит, предположение, что
,
неверно, то есть все собственные числа
должны являться корнями уравнения
.
Пусть
--
корень уравнения
.
Тогда базисный минор матрицы
не
может совпадать с определителем матрицы
и поэтому ![]() ,
, ![]() --
порядок матрицы
.
Уравнение (19.4)
является матричной записью однородной
системы линейных уравнений с
неизвестными
--
порядок матрицы
.
Уравнение (19.4)
является матричной записью однородной
системы линейных уравнений с
неизвестными ![]() ,
являющимися элементами матрицы-столбца
.
По теореме
15.3 число
решений в фундаментальной системе
решений равно
,
являющимися элементами матрицы-столбца
.
По теореме
15.3 число
решений в фундаментальной системе
решений равно ![]() ,
что больше нуля. Таким образом,
система (19.4)
имеет хотя бы одно ненулевое решение,
то есть числу
соответствует
хотя бы один собственный вектор
матрицы
.
,
что больше нуля. Таким образом,
система (19.4)
имеет хотя бы одно ненулевое решение,
то есть числу
соответствует
хотя бы один собственный вектор
матрицы
.
Определитель ![]() является
многочленом степени
от
переменного
,
так как при вычислении определителя
никаких арифметических действий кроме
сложения, вычитания и умножения выполнять
не приходится.
является
многочленом степени
от
переменного
,
так как при вычислении определителя
никаких арифметических действий кроме
сложения, вычитания и умножения выполнять
не приходится.
Определение 19.5 Матрица называется характеристической матрицей матрицы , многочлен называется характеристическим многочленом матрицы , уравнение называется характеристическим уравнением матрицы .
Пример 19.10 Найдите собственные числа и собственные векторы матрицы
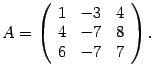
Решение. Составляем характеристическую матрицу :
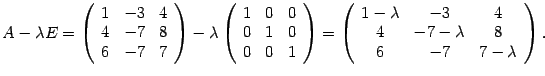
Находим характеристический многочлен
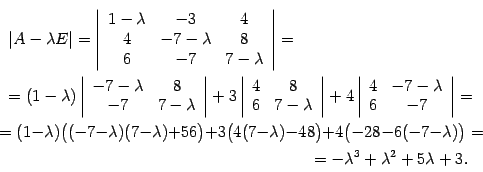
Решим характеристическое уравнение
![]()
Подбором
находим, что один корень уравнения
равен ![]() .
Есть теорема, которая говорит, что если
число
.
Есть теорема, которая говорит, что если
число ![]() является
корнем многочлена
является
корнем многочлена ![]() ,
то многочлен
делится
на разность
,
то многочлен
делится
на разность ![]() ,
то есть
,
то есть ![]() ,
где
,
где ![]() --
многочлен. В соответствии с этой теоремой
многочлен
--
многочлен. В соответствии с этой теоремой
многочлен ![]() должен
делиться на
должен
делиться на ![]() .
Выделим в характеристическом многочлене
этот множитель
.
Выделим в характеристическом многочлене
этот множитель ![]() :
:
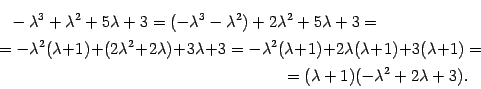
Находим
корни трехчлена ![]() .
Они равны
и
3. Таким образом,
.
Они равны
и
3. Таким образом,
![]()
![]() --
корень кратности 2 17.7 b,
--
корень кратности 2 17.7 b, ![]() --
простой корень. Итак, собственные числа
матрицы
равны
,
.
Найдем соответствующие им собственные
векторы.
--
простой корень. Итак, собственные числа
матрицы
равны
,
.
Найдем соответствующие им собственные
векторы.
Пусть ![]() ,
тогда для собственного вектора
получаем
матричное уравнение
,
тогда для собственного вектора
получаем
матричное уравнение
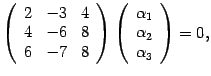
что соответствует системе уравнений
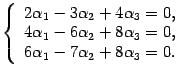
Решаем ее методом Гаусса (раздел "Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса)"). Выписываем расширенную матрицу системы
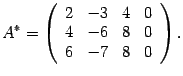
Первую
строку, умноженную на числа ![]() и
и ![]() прибавляем
соответственно ко второй и третьей
строкам
прибавляем
соответственно ко второй и третьей
строкам
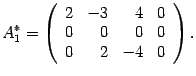
Меняем местами вторую и третью строки
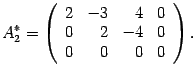
Возвращаемся к системе уравнений
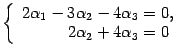
Базисный
минор матрицы ![]() находится
в первых двух столбцах и первых двух
строках, ранг равен 2. Поэтому фундаментальня
система содержит только одно решение.
Переменные
находится
в первых двух столбцах и первых двух
строках, ранг равен 2. Поэтому фундаментальня
система содержит только одно решение.
Переменные ![]() и
и ![]() оставляем
в левой части, а переменное
оставляем
в левой части, а переменное ![]() переносим
в правую часть
переносим
в правую часть
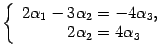
Полагаем ![]() ,
находим
,
находим ![]() ,
, ![]() .
Итак, собственному числу
соответствует
собственный вектор
.
Итак, собственному числу
соответствует
собственный вектор 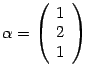 .
.
Пусть ![]() ,
тогда для собственного вектора
,
тогда для собственного вектора ![]() получаем
матричное уравнение
получаем
матричное уравнение
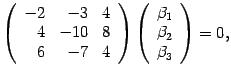
что соответствует системе уравнений
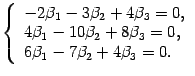
Решаем ее методом Гаусса. Выписываем расширенную матрицу
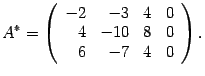
Первую строку умножаем на числа 2 и 3 и прибавляем соответственно ко второй и третьей строкам
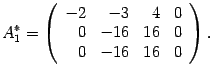
Вторую строку умножаем на и прибавляем к третьей
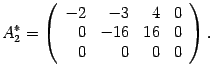
Возвращаемся к системе уравнений
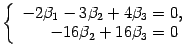
Базисный
минор матрицы
находится
в первых двух столбцах и первых двух
строках, ранг равен 2. Поэтому фундаментальная
система содержит только одно решение.
Переменные ![]() и
и ![]() оставляем
в левой части, а переменное
оставляем
в левой части, а переменное ![]() переносим
в правую часть
переносим
в правую часть
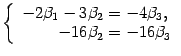
Полагаем ![]() ,
находим
,
находим ![]() ,
, ![]() .
Итак, собственному числу
соответствует
собственный вектор
.
Итак, собственному числу
соответствует
собственный вектор 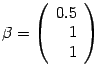 .
Чтобы избавиться от дроби, умножим
собственный вектор на 2, получим
собственный вектор с тем же самым
собственным числом. В итоге собственному
числу
соответствует
собственный вектор
.
Чтобы избавиться от дроби, умножим
собственный вектор на 2, получим
собственный вектор с тем же самым
собственным числом. В итоге собственному
числу
соответствует
собственный вектор 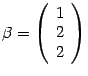 .
.
Ответ: Собственные числа: , , соответствующие собственные векторы: , .
9.
Приведение уравнений кривых второго порядка к каноническому виду
Укажем, как можно с помощью преобразований координат, рассмотренных в предыдущем параграфе, привести общее уравнение кривой второго порядка
к каноническим уравнениям эллипса, гиперболы или параболы, или к случаям их выражения. С помощью поворота осей координат на некоторый угол α всегда можно избавиться от члена с произведением координат. Действительно, подставляя в (47) вместо x и y их выражения по формуле (43), получим новое уравнение
коэффициент которого a'12 будет равен
Приравнивая коэффициент a'12 к нулю, получим тригонометрическое уравнение
Отсюда получаем
Далее, по формулам тригонометрии, получаем нужные нам значения для sin α и cos α :
Следовательно, уравнение кривой в новых координатах O'x'y' примет вид:
Если
в уравнении (50) Далее с помощью параллельного переноса системы координат O'x'y' уравнение (50) всегда можно привести к виду:
т.е. фактически к каноническому виду. Из уравнения (51) следует, что мы имеем либо эллипс (если a'11 и a'22 одного знака, а a"0противоположного), либо мнимое место точек (если a'11, a'22, a"0 имеют один знак), либо одну точку (если a'11 и a'22 имеют один знак, а a"0 = 0), либо гиперболу (если a'11 и a'22 разных знаков и a"0 ≠ 0), либо две пересекающие прямые (если a'11 и a'22 разных знаков и a"0 = 0). Если
же в уравнении (50) один из коэффициентов
a'11 и
a'22 ,
например, a'22 обращается
в нуль, то это уравнение с помощью
переноса осей приведется к каноническому
уравнению параболы Отсюда следует, что всякая кривая 2-го порядка есть либо эллипс, либо гипербола, либо парабола, либо представляет собой их "вырождение". Пример. Привести к каноническому виду уравнение кривой второго порядка 29x2 - 24xy + 36y2 + 82x - 96y - 91 = 0 и сделать чертеж. Решение. Здесь a11 = 29, a12 =-12, a22 = 36. Поэтому
решая
последнее уравнение, получим
И формулы преобразования координат запишутся в виде:
Подставляем выражения "старых" координат через "новые" в исходное уравнение кривой и, проделав достаточно громоздкие, но простые преобразования, получаем:
или, выделяя полный квадрат по x' и y' можем записать:
отсюда:
Введем
новые координаты
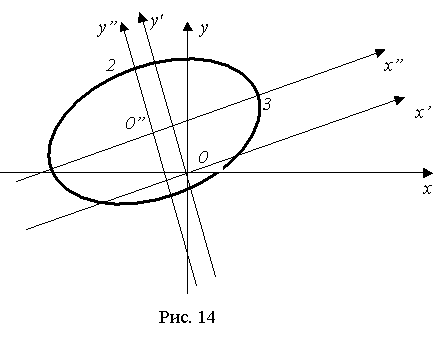
т.е. данная кривая есть эллипс с полуосями a = 3 и b = 2. Сделаем чертеж (рис. 14).
|
В этом разделе мы выясним, как по общему уравнению найти такую систему координат. Результаты этого раздела используются и для приведения общего уравнения кривой второго порядка к каноническому виду. Достаточно будет во всех рассуждениях отбросить третью координату.
Пусть
в пространстве задана прямоугольная
декартова система координат ![]() .
Рассмотрим общее уравнение поверхности
второго порядка, коэффициенты в котором
обозначены специальным образом
.
Рассмотрим общее уравнение поверхности
второго порядка, коэффициенты в котором
обозначены специальным образом
|
(19.7) |
где ![]() --
числа, причем хотя бы одно из чисел
--
числа, причем хотя бы одно из чисел ![]() отлично
от нуля.
отлично
от нуля.
Выделим квадратичную часть выражения, стоящего в уравнении слева,
![]()
Такое выражение называется квадратичной формой от трех переменных. Составим матрицу
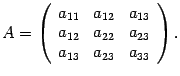
Эта
матрица называется матрицей
квадратичной формы ![]() .
Она является симметричной,
то есть
.
Она является симметричной,
то есть ![]() ,
или, другими словами,
,
или, другими словами, ![]() .
Следует обратить внимание на то, как
эта матрица составлена. На диагонали у
нее стоят коэффициенты при квадратах
переменных, а в остальных местах --
половины коэффициентов при произведениях
переменных.
.
Следует обратить внимание на то, как
эта матрица составлена. На диагонали у
нее стоят коэффициенты при квадратах
переменных, а в остальных местах --
половины коэффициентов при произведениях
переменных.
Исходная
система координат является прямоугольной,
поэтому скалярное произведение векторов
с координатными столбцами 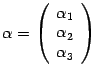 ,
, 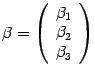 задается
формулой
задается
формулой ![]() .
Сформулируем две теоремы, позволяющие
пользоваться приведенным ниже алгоритмом.
.
Сформулируем две теоремы, позволяющие
пользоваться приведенным ниже алгоритмом.
Теорема 19.4 Если матрица -- симметричная, то ее собственные числа являются вещественными числами и существует ортонормированный базис из собственных векторов.
Пусть
--
матрица квадратичной формы
.
По сформулированной теореме у нее
существует ортонормированный базис из
собственных векторов. Обозначим
их ![]() ,
, ![]() ,
, ![]() ,
и пусть эти векторы имеют координаты
,
и пусть эти векторы имеют координаты
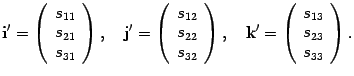
Базис i, j, k назовем
старым, а базис ![]() --
новым. Тогда матрица перехода 19.1.4.а
будет иметь вид
--
новым. Тогда матрица перехода 19.1.4.а
будет иметь вид
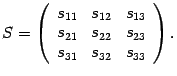
Выберем
новую систему координат ![]() так,
что начало координат не изменяется, а
новые базисные векторы
,
,
задают
направления новых координатных
осей
так,
что начало координат не изменяется, а
новые базисные векторы
,
,
задают
направления новых координатных
осей ![]() ,
, ![]() ,
, ![]() (рис.
19.8).
(рис.
19.8).
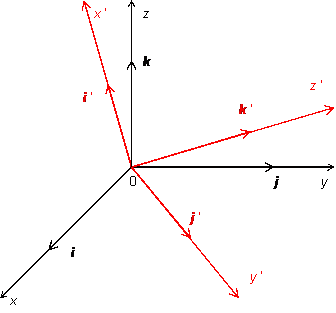
Рис.19.8.Система координат
Тогда
координаты ![]() точки
точки ![]() являются
координатами ее радиус-вектора
являются
координатами ее радиус-вектора ![]() и,
следовательно, при замене базиса меняются
по формуле (18.1)
и,
следовательно, при замене базиса меняются
по формуле (18.1)
|
(19.8) |
Теорема 19.5 Пусть
собственные векторы
,
,
матрицы
квадратичной формы
,
образующие ортонормированный базис,
соответствуют собственным числам ![]() ,
, ![]() ,
, ![]() .
Тогда в системе координат
квадратичная
форма принимает вид
.
Тогда в системе координат
квадратичная
форма принимает вид
![]()
Если
мы из равенства (19.8)
выпишем выражение ![]() ,
, ![]() ,
, ![]() через
новые переменные
через
новые переменные ![]() ,
, ![]() ,
, ![]() и
подставим в уравнение (19.7),
то обнаружим, что квадратичная его часть
и линейная часть преобразуются независимо
друг от друга. В результате уравнение
в системе координат
имеет
вид
и
подставим в уравнение (19.7),
то обнаружим, что квадратичная его часть
и линейная часть преобразуются независимо
друг от друга. В результате уравнение
в системе координат
имеет
вид
|
(19.9) |
Хотя бы одно из чисел , , отлично от нуля, иначе матрица была бы нулевой.
Рассмотрим три случая.
Пусть все собственные числа , , отличны от нуля. В уравнении (19.9) выделим полные квадраты
![]()
Выполним
параллельный перенос системы координат
,
взяв за новое начало системы координат
точку ![]() (см.
формулы (13.21)).
Тогда в новой системе координат
(см.
формулы (13.21)).
Тогда в новой системе координат ![]() уравнение
запишется в виде
уравнение
запишется в виде
![]()
Здесь возможны следующие варианты.
Пусть
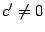 .
Перенесем
.
Перенесем 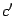 в
правую часть и поделим обе части на
в
правую часть и поделим обе части на 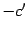 ,
получим
,
получим
![]()
Если числа
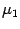 ,
, 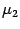 ,
, 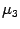 отрицательны,
то ни одна точка пространства не
удовлетворяет этому уравнению. Говорят,
что оно определяет мнимый
эллипсоид.
отрицательны,
то ни одна точка пространства не
удовлетворяет этому уравнению. Говорят,
что оно определяет мнимый
эллипсоид.Если числа , , положительны, то уравнение является каноническим уравнением эллипсоида.
Если одно из чисел , , отрицательно, а остальные положительны, то (после переименования осей) получим каноническое уравнение однополостного гиперболоида.
Если одно из чисел , , положительно, остальные отрицательны, то (после переименования осей) получим каноническое уравнение двуполостного гиперболоида.
Пусть
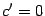 .
.Если все числа , , положительны, то только начало координат удовлетворяет этому уравнению. Поверхность выродилась в точку.
Если одно из чисел , , отрицательно, а два положительны, то (после переименования осей) получим каноническое уравнение конуса.
Если же два числа отрицательны или все три отрицательны, то, умножив обе части уравнения на , получим случай 2 или случай 1.
Пусть одно из чисел , , равно нулю, а два других отличны от нуля. Допустим, что
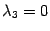 .
Тогда в уравнении (19.9)
выделим полные квадраты по переменным
,
.
Тогда в уравнении (19.9)
выделим полные квадраты по переменным
,
![]()
Пусть
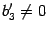 .
Преобразуем уравнение к виду
.
Преобразуем уравнение к виду
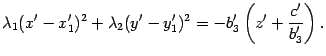
Поделим
обе части уравнения на ![]() и
выполним параллельный перенос осей
координат, взяв за новое начало координат
точку
и
выполним параллельный перенос осей
координат, взяв за новое начало координат
точку ![]() .
Получим уравнение
.
Получим уравнение
![]()
Если числа и положительны, то это -- каноническое уравнение эллиптического параболоида.
Если
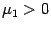 ,
, 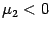 ,
получим каноническое уравнение
гиперболического параболоида.
,
получим каноническое уравнение
гиперболического параболоида.
Если
числа
и
отрицательны
или ![]() ,
, ![]() ,
то сменим направление у оси
,
то сменим направление у оси ![]() на
противоположное и получим либо случай 1,
либо случай 2.
на
противоположное и получим либо случай 1,
либо случай 2.
Пусть
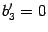 .
Тогда поверхность является цилиндрической,
образующие которой параллельны оси
,
а направляющей служит кривая на
плоскости
.
Тогда поверхность является цилиндрической,
образующие которой параллельны оси
,
а направляющей служит кривая на
плоскости 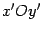 с
уравнением
с
уравнением
![]()
Анализ поверхностей с таким уравнением предоставляем читателю.
Пусть только одно из чисел , , отлично от нуля. Допустим, что
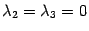 .
Тогда в уравнении (19.9)
выделим полный квадрат по переменному
.
Тогда в уравнении (19.9)
выделим полный квадрат по переменному
![]()
Пусть хотя бы одно из чисел
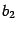 ,
, 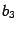 отлично
от нуля. Тогда на плоскости
отлично
от нуля. Тогда на плоскости 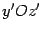 возьмем
две перпендикулярные прямые
возьмем
две перпендикулярные прямые 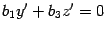 и
и 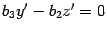 .
Возьмем новую систему координат, у
которой начало будет в точке
.
Возьмем новую систему координат, у
которой начало будет в точке 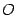 ,
ось
,
ось 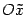 направлена
по оси
,
ось
направлена
по оси
,
ось 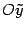 направлена
вдоль второй прямой, а ось
направлена
вдоль второй прямой, а ось 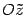 направлена
вдоль первой прямой. Тогда уравнение
примет вид
направлена
вдоль первой прямой. Тогда уравнение
примет вид
![]()
Это
-- уравнение цилиндрической поверхности,
образующие которой параллельны оси
,
а направляющей служит кривая на
плоскости ![]() с
уравнением
с
уравнением
Анализ возможных поверхностей оставляем читателю.
Пусть
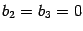 .
Тогда уравнение принимает вид
.
Тогда уравнение принимает вид
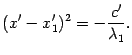
Если число справа положительно, то уравнение определяет две плоскости
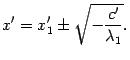
Если число справа равно нулю, то уравнение определяет одну плоскость
![]()
Если число справа отрицательно, то ни одна точка пространства уравнению не удовлетворяет.
Итак, получен алгоритм, позволяющий установить, какая поверхность задается уравнением второго порядка и каково ее положение в пространстве.
Пример 19.11 Приведите уравнение поверхности
![]()
к каноническому виду.
Решение. Квадратичная форма имеет вид
![]()
Выписываем ее матрицу
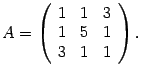
Находим ее собственные числа. Для этого запишем характеристическое уравнение
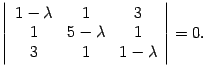
После вычисления определителя получим
![]()
Подбором
находим один корень ![]() .
Преобразуем уравнение, выделяя множитель
.
Преобразуем уравнение, выделяя множитель ![]()
![]()
или
![]()
откуда
![]()
Находим
два других корня характеристического
уравнения ![]() и
и ![]() .
.
Находим собственные векторы. Для собственного числа для координат собственного вектора получим систему уравнений
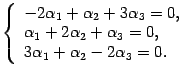
Решая
ее находим, что фундаментальная система
решений содержит только одно решение,
и в качестве собственного вектора можно
взять 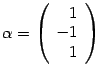 .
Для собственного числа
для
координат собственного вектора
получим
систему уравнений
.
Для собственного числа
для
координат собственного вектора
получим
систему уравнений
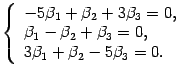
Отсюда
находим собственный вектор 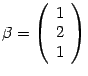 .
Для собственного числа
для
координат собственного вектора
.
Для собственного числа
для
координат собственного вектора ![]() получим
систему уравнений
получим
систему уравнений
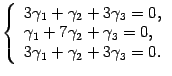
Отсюда
находим собственный вектор 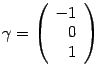 .
.
Легко
проверить, что ![]() ,
то есть собственные векторы попарно
ортогональны. Их длины равны
соответственно
,
то есть собственные векторы попарно
ортогональны. Их длины равны
соответственно ![]() ,
, ![]() ,
, ![]() .
Поэтому векторы нового ортонормированного
базиса будут иметь координаты
.
Поэтому векторы нового ортонормированного
базиса будут иметь координаты
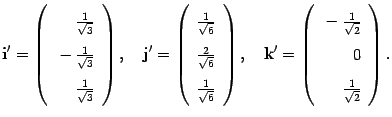
Матрица перехода имеет вид
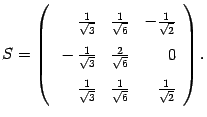
Старые
координаты связаны с новыми уравнением 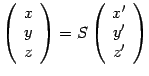 ,
то есть
,
то есть
|
(19.10) |
Подставим эти выражения в исходное уравнение. Квадратичная форма примет вид, в котором произведения переменных будут отсутствовать, а коэффициентами при квадратах будут служить собственные числа
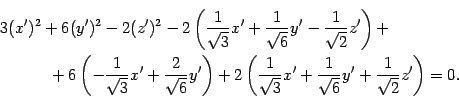
Приводим подобные члены
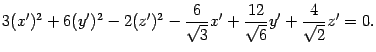
Выделим полные квадраты
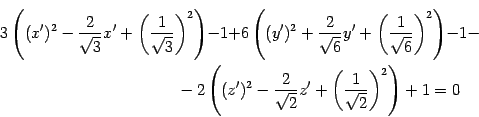
или
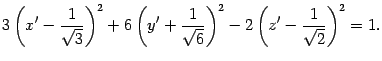
Выполняем параллельный перенос осей координат
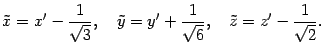
Новое
начало системы координат ![]() имеет
координаты
имеет
координаты
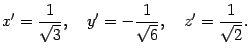
В исходной системе координат точка в соответствии с формулами (19.10) имеет координаты
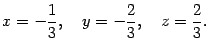
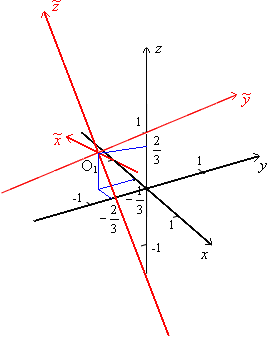
Рис.19.9.Система
координат ![]()
В новой системе координат (рис. 19.9) уравнение принимает канонический вид
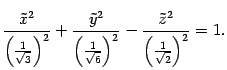
Это
уравнение является каноническим
уравнением однополостного гиперболоида.
Его центр находится в точке
,
две вещественные оси параллельны
векторам
,
,
вещественные полуоси равны ![]() ,
, ![]() .
Мнимая ось параллельна вектору
,
мнимая полуось равна
.
Мнимая ось параллельна вектору
,
мнимая полуось равна ![]() .
Изображение гиперболоида приведено на
рисунке 19.10.
.
Изображение гиперболоида приведено на
рисунке 19.10.
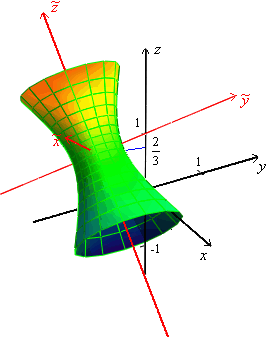
Рис.19.10.Изображение гиперболоида
10.
|
Дана прямоугольная матрица
Выделим в этой матрице k произвольных строк и k произвольных столбцов. Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы А.
Матрица А имеет Сkm·Сkn миноров k-го порядка.
Рассмотрим всевозможные миноры матрицы А, отличные от нуля.
Рангом матрицы А называется наибольший порядок невырожденного минора этой матрицы. Если матрица нулевая, то ранг ее принимается равным нулю.
Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы.
Ранг матрицы А обозначается r(A). Если r(A) = r(B), то матрицы А и В называются эквивалентными. В этом случае пишут А ~ В.
Под элементарными преобразованиями матрицы понимают: 1) замену строк столбцами, а столбцов - соответствующими строками; 2) перестановку строк; 3) вычеркивание строки, все элементы которой равны нулю; 4) умножение какой-либо строки на число, отличное от нуля; 5) прибавление к элементам одной строки соответствующих элементов другой. Пример. Найти ранг матрицы
Решение. Первую строку перепишем. От элементов второй строки вычтем соответствующие элементы первой строки и запишем во вторую строку. От элементов третьей строки вычтем соответствующие элементы первой строки, умноженные на 5. Четвертую строку перепишем.
Первую строку перепишем. Вторую и третью строки разделим на 2 и запишем соответственно на место второй и третьей строки. Четвертую строку перепишем.
Первую, вторую и червертую строки перепишем. На место третьей строки поставим разность третьей и второй, умноженной на 3.
Первую, вторую и червертую строки перепишем. Третью строку разделим на (-4).
От первой строки отнимем четвертую, умноженную на 3. Вторую строку перепишем. На место третьей строки поставим четвертую. На место четвертой строки поставим разность третьей и четвертой.
От первой строки вычтем четвертую, умноженную на 2. От второй строки вычтем четвертую. Третью и четвертую строки перепишем.
Ранг данной матрицы равен 4, т.к. получили единичную квадратную матрицу четвертого порядка (определитель единичной матрицы всегда равен 1, т.е. отличен от нуля, что по определению означает, что матрица невырожденная). |
11.