Понятие матрицы

Основные понятия и обозначения. Пусть m и n два произвольных натуральных числа.Матрицей размера m на n (записывается так   )называется совокупность mn вещественных (комплексных) чисел или элементов другой структуры (многочлены, функции и т.д.), записанных в виде прямоугольной таблицы, которая состоит из m строк и n столбцов и взятая в круглые или прямоугольные или в двойные прямые скобки. При этом сами числа называются элементами матрицы и каждому элементу ставится в соответствие два числа -номер строки и номер столбца.

Для обозначения матрицы используются прописные латинские буквы, при этом саму матрицу заключают в круглые или прямоугольные или в двойные прямые скобки. Элементы матрицыобозначают строчными латинскими буквами, снабженными двумя индексами:   - элемент матрицы, расположенный в i-й строке и j-м столбце или коротко элемент в позиции (i,j). В общем виде матрица размера m на n может быть записана следующим образом

Приведём некоторые обозначения, которыми будем пользоваться в дальнейшем:

 - множество всех матриц размера m на n;

 - матрица A с элементами   в позиции (i,j);

 - матрица размера m на n.

Элементы   , где i=j, называются диагональными, а элементы   , где   - внедиагональными. Совокупность диагональных элементов   , где k = min (m,n), называется главной диагональю матрицы.

Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается символом O.

Заметим, что для каждого размера   существует своя нулевая матрица.

Матрица размера n на n называется квадратной матрицей n-го порядка, т.е. число строк равно числу столбцов.

Квадратная матрица называется диагональной, если все ее внедиагональные элементы равны нулю.

Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной матрицей и обозначается символом I или E.

Матрица размера   называется матрицей-строкой или вектор-строкой. Матрица размера   называется матрицей столбцом или вектор-столбцом. 

Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.

Матрицы (и соответственно математический раздел - матричная алгебра) имеют важное значение в прикладной математике, так как позволяют записать в достаточно простой форме значительную часть математических моделей объектов и процессов. Термин "матрица" появился в 1850 году. Впервые упоминались матрицы еще в древнем Китае, позднее у арабских математиков.

Матрицей A=A_mn порядка m*n называется прямоугольная таблица чисел, содержащая m - строк и n - столбцов.

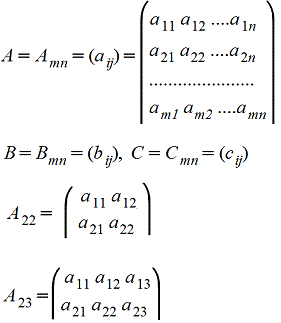
Элементы матрицы a_ij, у которых i=j, называются диагональными и образуют главную диагональ.

Для квадратной матрицы (m=n) главную диагональ образуют элементы a₁₁, a₂₂,..., a_nn .

Равенство матриц.

A=B, если порядки матриц A и B одинаковы и a_ij=b_ij (i=1,2,...,m; j=1,2,...,n)

Действия над матрицами.

1. Сложение матриц - поэлементная операция

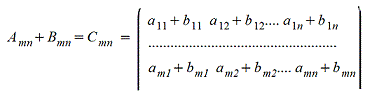
2. Вычитание матриц - поэлементная операция

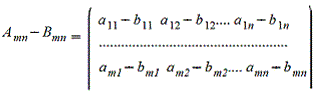
3. Произведение матрицы на число - поэлементная операция

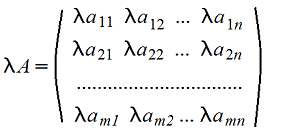
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

A_mk*B_kn=C_mn причем каждый элемент с_ij матрицы C_mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.

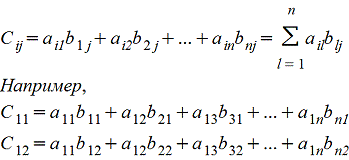
Покажем операцию умножения матриц на примере

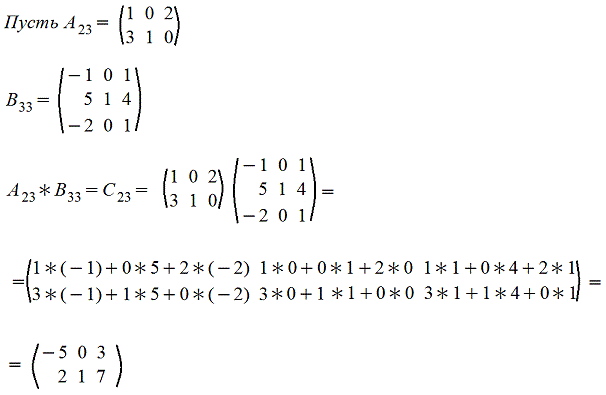
5. Возведение в степень

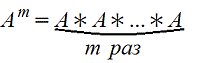
m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц

6. Транспонирование матрицы А. Транспонированную матрицу обозначают A^T или A'

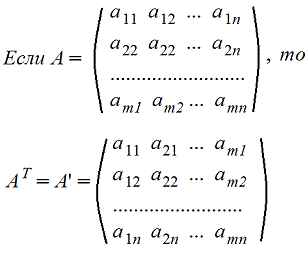
Строки и столбцы поменялись местами

Пример

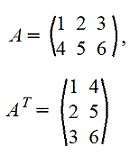
Свойства опрераций над матрицами

A+B=B+A

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(A')'=A

(λA)'=λ(A)'

(A+B)'=A'+B'

(AB)'=B'A'

Виды матриц

1. Прямоугольные: m и n - произвольные положительные целые числа

2. Квадратные: m=n

3. Матрица строка: m=1. Например, (1 3 5 7 ) - во многих практических задачах такая матрица называется вектором

4. Матрица столбец: n=1. Например

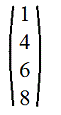
5. Диагональная матрица: m=n и a_ij=0, если i≠j. Например

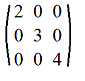
6. Единичная матрица: m=n и

7. Нулевая матрица: a_ij=0, i=1,2,...,m

j=1,2,...,n

8. Треугольная матрица: все элементы ниже главной диагонали равны 0.

Пример.

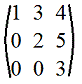
9. Симметрическая матрица: m=n и a_ij=a_ji (т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно A'=A

Например,

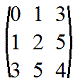
10. Кососимметрическая матрица: m=n и a_ij=-a_ji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем a_ii=-a_ii)

Пример.

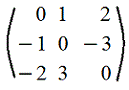
Ясно, A'=-A

11. Эрмитова матрица: m=n и a_ii=-ã_ii (ã_ji - комплексно - сопряженное к a_ji, т.е. если A=3+2i, то комплексно - сопряженное Ã=3-2i)

Пример

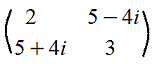
5. Умноже́ние ма́триц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведе́нием ма́триц.

Пусть даны две прямоугольные матрицы   и   размерности   и   соответственно:

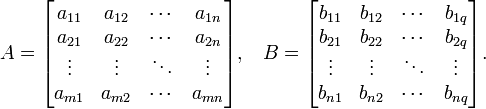
Тогда матрица   размерностью   называется их произведением:

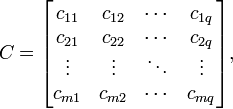
где:

Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.

Следует заметить, что из существования произведения   вовсе не следует существование произведения 

Произведение матриц AB состоит из всех возможных комбинаций скалярных произведений строк матрицы A и столбцов матрицы B. Элемент матрицы AB с индексами i, jесть скалярное произведение i-ой строки матрицы A и j-го столбца матрицы B.

Иллюстрация справа демонстрирует вычисление произведения двух матриц A и B, она показывает как каждые пересечения в произведении матриц соответствуют строкам матрицы A и столбцам матрицы B. Размер результирующей матрицы всегда максимально возможный, то есть для каждой строки матрицы A и столбца матрицы B есть всегда соответствующее пересечение в произведении матрицы.

Значения на пересечениях отмеченных кружочками будут:

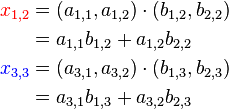
В общем случае, произведение матриц не является коммутативной операцией. К примеру:

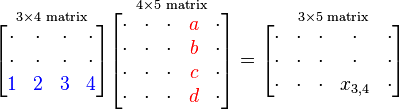
Элемент   произведения матриц приведённых выше вычисляется следующим образом

Первая координата в обозначении матрицы обозначает строку, вторая координата — столбец; этот порядок используют как при индексации, так и при обозначении размера. Элемент   на пересечении строки   и столбца  результирующей матрицы является скалярным произведением  -й строки первой матрицы и  -го столбца второй матрицы. Это объясняет почему ширина и высота умножаемых матриц должны совпадать: в противном случае скалярное произведение не определено.

Сочетательное свойство:

Распределительное свойство:

.

Произведение матрицы на единичную матрицу   подходящего порядка равно самой матрице:

Произведение матрицы на нулевую матрицу   подходящей размерности равно нулевой матрице:

Если   и   — квадратные матрицы одного и того же порядка, то произведение матриц обладает ещё рядом свойств.

Умножение матриц в целом некоммутативно:

Если  , то матрицы   и   называются перестановочными или коммутирующими между собой.

Определитель и след произведения не зависят от порядка умножения матриц:

6.

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E: