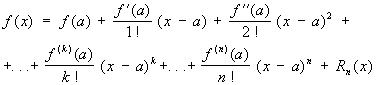- •Как вычислить определитель?
- •Свойства определителей
- •Описание метода
- •Понятие матрицы
- •Как найти обратную матрицу?
- •Решение системы линейных уравнений матричным методом
- •Решение произвольных систем линейных уравнений
- •Метод последовательного исключения неизвестных (метод Гаусса)
- •Переход к другому базису
- •Нахождение опорных решений
- •1. Прямоугольная система координат в пространстве
- •Деление отрезка в заданном отношении. Координаты середины отрезка. Определение площади треугольника по известным координатам его вершин. Площадь многоугольника
- •Свободные, скользящие и фиксированные векторы
- •1. Векторы, действия над векторами.
- •1) Сложение векторов.
- •2) Вычитание векторов.
- •3) Умножение вектора на число.
- •2. Координаты вектора
- •3. Базис системы векторов.
- •Пример.
- •Скалярное произведение векторов
- •Векторное произведение векторов
- •Смешанное произведение векторов
- •Геометрический смысл смешанного произведения
- •Свойства смешанного произведения:
- •Теорема 6. Всякая элементарная функция непрерывна в каждой точке, в которой она определена. Первый замечательный предел
- •Модификации первого замечательного предела
- •Второй замечательный предел
- •*3) Бесконечно малые величины
- •*4) Непрерывные функции Определения
- •Типы разрывов
- •5)Производная, правила и формулы дифференцирования
- •6)Правила дифференцирования
- •11Уравнение касательной и нормали
- •12. Производные высших порядков
- •13. Дифференциалы высших порядков и их неинвариантность
- •Основные дифференциалы
- •14. Теоремы Ролля, Лагранжа, Коши
- •15.Ряды Тейлора,Маклорена
- •16. Правило Лопиталя
- •17. Возрастание и убывание функции на интервале, экстремумы.
- •Необходимые определения.
- •Достаточные признаки возрастания и убывания функции.
- •Достаточные признаки экстремума функции.
- •18. Выпуклость, вогнутость и точки перегиба функции
- •19.Асимптоты
- •2. Нахождение асимптоты
- •2.1 Геометрический смысл асимптоты
- •2.2 Общий метод отыскания асимптоты
- •3.1 Горизонтальная асимптота
- •3.2 Вертикальная асимптота(рис.4)
- •3.3 Наклонная асимптота
- •20. Построение графика квадратичной функции по направлению ветвей, характерным точкам и оси симметрии параболы Примеры:
3.1 Горизонтальная асимптота
Пусть lim f (x) = b. Тогда говорят, что у функции f (x) имеется горизонтальная асимптота y = b. График функции чаще всего имеет такой вид (при x +)
хотя в принципе, может иметь и такой вид
3.2 Вертикальная асимптота(рис.4)
Пусть при x a 0 lim f (x) = . Тогда говорят, что прямая x = a является
х
вертикальной асимптотой f (x). График функции f (x) при приближении x к а ведёт примерно так хотя, конечно, могут быть разные варианты, связанные с тем, куда уходит f (x) в + или .
Чаще всего вертикальная асимптота появляется тогда, когда f (x) имеет вид
.
Тогда вертикальные асимптоты находятся как корни уравнения
3.3 Наклонная асимптота
Пусть уравнение асимптот есть y = ax + b. Значение функции при аргументе х есть d = ax + b - f (x). Неограниченное приближение к асимптоте означает, что величина d = ax + b - f (x) стремится к 0 при х
lim [f (x) - (ax + b)] = 0.
x
Если эта величина стремится к нулю, то тем более стремится к нулю величина
Но тогда мы имеем
и так как последний предел равен нулю, то
Зная а, можно найти и b из исходного соотношения
Тем самым параметры асимптоты полностью определяются.
Пример
то есть асимптота при x + имеет уравнение y=x.
Аналогично можно показать, что при x - асимптота имеет вид y = - x.
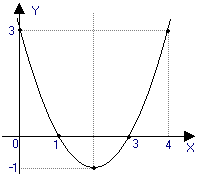
20. Построение графика квадратичной функции по направлению ветвей, характерным точкам и оси симметрии параболы Примеры:
|
y = x2 - 4x + 3
|
|
y= -x2 - 6x - 9
|
|
22.Формула Тейлора
|
формула
изображающая функцию f (x), имеющую n-ю производную f (n)(a) в точке х = а, в виде суммы многочлена степени n, расположенного по степеням х—а, и остаточного члена Rn (x), являющегося в окрестности точки а бесконечно малой более высокого порядка, чем (x—a) n [то есть Rn (x) = an (x)(x—a) n, где an (x) ® 0 при х ® а]. Если в интервале между а и х существует (n + 1)-я производная, то Rn (x)можно представить в видах:
где x и x1 — какие-то точки указанного интервала (остаточный член Т. ф. в формах Лагранжа и соответственно Коши). График многочлена, входящего в Т. ф.. имеет в точке а соприкосновение не ниже n-го порядка с графиком функции f (x). Т. ф. применяют для исследования функций и для приближённых вычислений. |