
- •Как вычислить определитель?
- •Свойства определителей
- •Описание метода
- •Понятие матрицы
- •Как найти обратную матрицу?
- •Решение системы линейных уравнений матричным методом
- •Решение произвольных систем линейных уравнений
- •Метод последовательного исключения неизвестных (метод Гаусса)
- •Переход к другому базису
- •Нахождение опорных решений
- •1. Прямоугольная система координат в пространстве
- •Деление отрезка в заданном отношении. Координаты середины отрезка. Определение площади треугольника по известным координатам его вершин. Площадь многоугольника
- •Свободные, скользящие и фиксированные векторы
- •1. Векторы, действия над векторами.
- •1) Сложение векторов.
- •2) Вычитание векторов.
- •3) Умножение вектора на число.
- •2. Координаты вектора
- •3. Базис системы векторов.
- •Пример.
- •Скалярное произведение векторов
- •Векторное произведение векторов
- •Смешанное произведение векторов
- •Геометрический смысл смешанного произведения
- •Свойства смешанного произведения:
- •Теорема 6. Всякая элементарная функция непрерывна в каждой точке, в которой она определена. Первый замечательный предел
- •Модификации первого замечательного предела
- •Второй замечательный предел
- •*3) Бесконечно малые величины
- •*4) Непрерывные функции Определения
- •Типы разрывов
- •5)Производная, правила и формулы дифференцирования
- •6)Правила дифференцирования
- •11Уравнение касательной и нормали
- •12. Производные высших порядков
- •13. Дифференциалы высших порядков и их неинвариантность
- •Основные дифференциалы
- •14. Теоремы Ролля, Лагранжа, Коши
- •15.Ряды Тейлора,Маклорена
- •16. Правило Лопиталя
- •17. Возрастание и убывание функции на интервале, экстремумы.
- •Необходимые определения.
- •Достаточные признаки возрастания и убывания функции.
- •Достаточные признаки экстремума функции.
- •18. Выпуклость, вогнутость и точки перегиба функции
- •19.Асимптоты
- •2. Нахождение асимптоты
- •2.1 Геометрический смысл асимптоты
- •2.2 Общий метод отыскания асимптоты
- •3.1 Горизонтальная асимптота
- •3.2 Вертикальная асимптота(рис.4)
- •3.3 Наклонная асимптота
- •20. Построение графика квадратичной функции по направлению ветвей, характерным точкам и оси симметрии параболы Примеры:
Свойства определителей
СВОЙСТВО 1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером, то есть
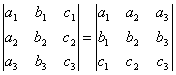 .
.
СВОЙСТВО 2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1. Например,
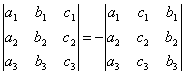 .
.
СВОЙСТВО 3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.
СВОЙСТВО 4. Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k. Например,
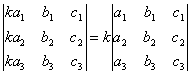 .
.
СВОЙСТВО 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случае предыдущего (при k=0).
СВОЙСТВО 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.
СВОЙСТВО 7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же. Например,
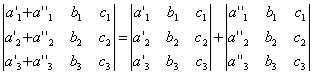
СВОЙСТВО 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится. Например,
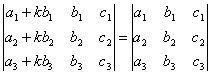 .
.
Дальнейшие свойства определителей связаны с понятием алгебраического дополнения и минора. Минором некоторого элемента называется определитель, получаемый из данного путем вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.
Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число нечетное.
Алгебраическое дополнение элемента мы будем обозначать большой буквой того же наименования и тем же номером, что и буква, кторой обозначен сам элемент.
СВОЙСТВО 9. Определитель
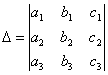
равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения.
Иначе говоря, имеют место следующие равенства:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
3.
|
Описание метода
Для
системы ![]() линейных
уравнений с
неизвестными
(над произвольным полем)
линейных
уравнений с
неизвестными
(над произвольным полем)
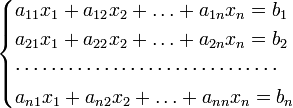
с
определителем матрицы системы ![]() ,
отличным от нуля, решение записывается
в виде
,
отличным от нуля, решение записывается
в виде
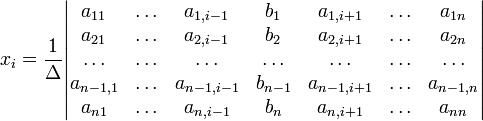
(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:
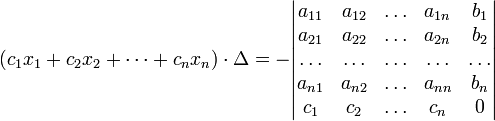
В
этой форме формула Крамера справедлива
без предположения, что
отлично
от нуля, не нужно даже, чтобы коэффициенты
системы были бы элементами целостного
кольца (определитель
системы может быть даже делителем нуля
в кольце коэффициентов). Можно также
считать, что либо наборы ![]() и
и ![]() ,
либо набор
,
либо набор ![]() состоят
не из элементов кольца коэффициентов
системы, а какого-нибудь модуля над
этим кольцом. В этом виде формула Крамера
используется, например, при доказательстве
формулы для определителя
Грама и Леммы
Накаямы.
состоят
не из элементов кольца коэффициентов
системы, а какого-нибудь модуля над
этим кольцом. В этом виде формула Крамера
используется, например, при доказательстве
формулы для определителя
Грама и Леммы
Накаямы.
Пример
Система линейных уравнений:
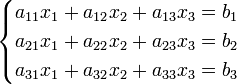
Определители:
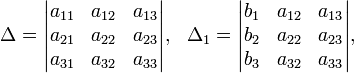
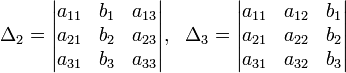
Решение:
![]()
Пример:
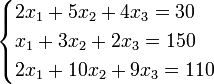
Определители:
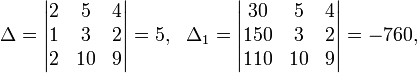
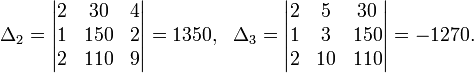
![]()
4.
