
- •Как вычислить определитель?
- •Свойства определителей
- •Описание метода
- •Понятие матрицы
- •Как найти обратную матрицу?
- •Решение системы линейных уравнений матричным методом
- •Решение произвольных систем линейных уравнений
- •Метод последовательного исключения неизвестных (метод Гаусса)
- •Переход к другому базису
- •Нахождение опорных решений
- •1. Прямоугольная система координат в пространстве
- •Деление отрезка в заданном отношении. Координаты середины отрезка. Определение площади треугольника по известным координатам его вершин. Площадь многоугольника
- •Свободные, скользящие и фиксированные векторы
- •1. Векторы, действия над векторами.
- •1) Сложение векторов.
- •2) Вычитание векторов.
- •3) Умножение вектора на число.
- •2. Координаты вектора
- •3. Базис системы векторов.
- •Пример.
- •Скалярное произведение векторов
- •Векторное произведение векторов
- •Смешанное произведение векторов
- •Геометрический смысл смешанного произведения
- •Свойства смешанного произведения:
- •Теорема 6. Всякая элементарная функция непрерывна в каждой точке, в которой она определена. Первый замечательный предел
- •Модификации первого замечательного предела
- •Второй замечательный предел
- •*3) Бесконечно малые величины
- •*4) Непрерывные функции Определения
- •Типы разрывов
- •5)Производная, правила и формулы дифференцирования
- •6)Правила дифференцирования
- •11Уравнение касательной и нормали
- •12. Производные высших порядков
- •13. Дифференциалы высших порядков и их неинвариантность
- •Основные дифференциалы
- •14. Теоремы Ролля, Лагранжа, Коши
- •15.Ряды Тейлора,Маклорена
- •16. Правило Лопиталя
- •17. Возрастание и убывание функции на интервале, экстремумы.
- •Необходимые определения.
- •Достаточные признаки возрастания и убывания функции.
- •Достаточные признаки экстремума функции.
- •18. Выпуклость, вогнутость и точки перегиба функции
- •19.Асимптоты
- •2. Нахождение асимптоты
- •2.1 Геометрический смысл асимптоты
- •2.2 Общий метод отыскания асимптоты
- •3.1 Горизонтальная асимптота
- •3.2 Вертикальная асимптота(рис.4)
- •3.3 Наклонная асимптота
- •20. Построение графика квадратичной функции по направлению ветвей, характерным точкам и оси симметрии параболы Примеры:
17. Возрастание и убывание функции на интервале, экстремумы.
Очень важную информацию о поведении функции предоставляют промежутки возрастания и убывания. Их нахождение является частью процесса исследования функции и построения графика. К тому же точкам экстремума, в которых происходит смена с возрастания на убывание или с убывания на возрастание, уделяется особое внимание при нахождении наибольшего и наименьшего значения функции на некотором интервале. В этой статье дадим необходимые определения, сформулируем достаточный признак возрастания и убывания функции на интервале и достаточные условия существования экстремума, применим всю эту теорию к решению примеров и задач. Рекомендуем при необходимости обращаться к разделу дифференцирование функции, так как все признаки в этой статье основаны на нахождении производной.
Необходимые определения.
Определение
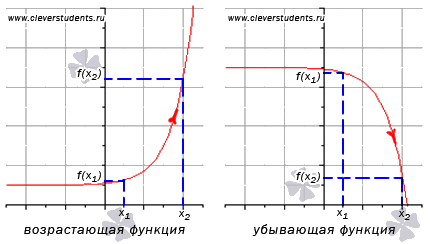
возрастающей функции.
Функция
y = f(x)
возрастает на интервале X,
если для любых
![]() и
и
![]() выполняется
неравенство
выполняется
неравенство
![]() .
Другими словами – большему значению
аргумента соответствует большее значение
функции.
Определение
убывающей функции.
Функция
y = f(x)
убывает на интервале X,
если для любых
и
.
Другими словами – большему значению
аргумента соответствует большее значение
функции.
Определение
убывающей функции.
Функция
y = f(x)
убывает на интервале X,
если для любых
и
![]() выполняется
неравенство
выполняется
неравенство
![]() .
Другими словами – большему значению
аргумента соответствует меньшее значение
функции.
.
Другими словами – большему значению
аргумента соответствует меньшее значение
функции.
ЗАМЕЧАНИЕ:
если функция определена и непрерывна
в концах интервала возрастания или
убывания (a;
b), то есть
при x = a
и x = b,
то эти точки включаются в промежуток
возрастания или убывания. Это не
противоречит определениям возрастающей
и убывающей функции на промежутке X.
К
примеру, из свойств основных элементарных
функций мы знаем, что y
= sinx определена
и непрерывна для всех действительных
значений аргумента. Поэтому, из возрастания
функции синуса на интервале
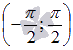 мы
можем утверждать о возрастании на
отрезке
мы
можем утверждать о возрастании на
отрезке
![]() .
Точку
.
Точку
![]() называют
точкой
максимума
функции y =
f(x), если для
всех x из ее окрестности справедливо
неравенство
называют
точкой
максимума
функции y =
f(x), если для
всех x из ее окрестности справедливо
неравенство
![]() .
Значение функции в точке максимума
называют максимумом
функции и
обозначают
.
Значение функции в точке максимума
называют максимумом
функции и
обозначают
![]() .
Точку
называют
точкой
минимума
функции y =
f(x), если для
всех x из ее окрестности справедливо
неравенство
.
Точку
называют
точкой
минимума
функции y =
f(x), если для
всех x из ее окрестности справедливо
неравенство
![]() .
Значение функции в точке минимума
называют минимумом
функции и
обозначают
.
Значение функции в точке минимума
называют минимумом
функции и
обозначают
![]() .
Под
окрестностью точки
понимают
интервал
.
Под
окрестностью точки
понимают
интервал
![]() ,
где
,
где
![]() -
достаточно малое положительное число.
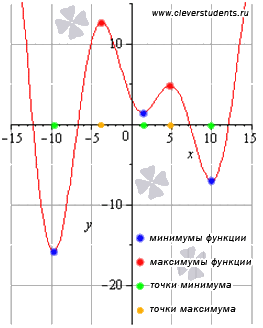
Точки минимума и максимума
называют точками
экстремума,
а значения функции, соответствующие
точкам экстремума, называют экстремумами
функции.
-
достаточно малое положительное число.
Точки минимума и максимума
называют точками
экстремума,
а значения функции, соответствующие
точкам экстремума, называют экстремумами
функции.
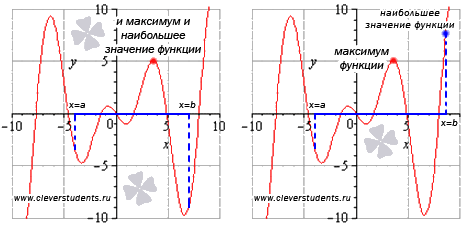
Не путайте экстремумы функции с наибольшим и наименьшим значением функции. На первом рисунке наибольшее значение функции на отрезке [a; b] достигается в точке максимума и равно максимуму функции, а на втором рисунке – наибольшее значение функции достигается в точке x = b, которая не является точкой максимума.
Достаточные признаки возрастания и убывания функции.
На основании достаточных признаков находятся промежутки возрастания и убывания функции. Вот формулировки признаков:
если производная функции y = f(x) положительна для любого x из интервала X, то функция возрастает на X;
если производная функции y = f(x) отрицательна для любого x из интервала X, то функция убывает на X.
Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:
найти область определения функции;
найти производную функции;
решить неравенства
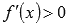 и
и
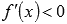 на
области определения;
на
области определения;
к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.
Рассмотрим
пример для разъяснения
алгоритма.
Пример.
Найти
промежутки возрастания и убывания
функции
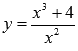 .
Решение.
Первым
шагом является нахождение обрасти
определения функции. В нашем примере
выражение в знаменателе не должно
обращаться в ноль, следовательно,
.
Решение.
Первым
шагом является нахождение обрасти
определения функции. В нашем примере
выражение в знаменателе не должно
обращаться в ноль, следовательно,
![]() .
Переходим
к производной функции:
.
Переходим
к производной функции:
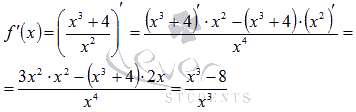 Для
определения промежутков возрастания
и убывания функции по достаточному
признаку решаем неравенства
Для
определения промежутков возрастания
и убывания функции по достаточному
признаку решаем неравенства
![]() и
и
![]() на
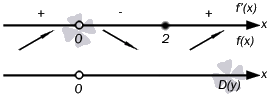
области определения. Воспользуемся
обобщением метода интервалов. Единственным
действительным корнем числителя является
x = 2,
а знаменатель обращается в ноль при x
= 0. Эти точки
разбивают область определения на
интервалы, в которых производная функции
сохраняет знак. Отметим эти точки на
числовой прямой. Плюсами и минусами
условно обозначим интервалы, на которых
производная положительна или отрицательна.
Стрелочки снизу схематично показывают
возрастание или убывание функции на
соответствующем интервале.
на
области определения. Воспользуемся
обобщением метода интервалов. Единственным
действительным корнем числителя является
x = 2,
а знаменатель обращается в ноль при x
= 0. Эти точки
разбивают область определения на
интервалы, в которых производная функции
сохраняет знак. Отметим эти точки на
числовой прямой. Плюсами и минусами
условно обозначим интервалы, на которых
производная положительна или отрицательна.
Стрелочки снизу схематично показывают
возрастание или убывание функции на
соответствующем интервале.
 Таким
образом,
Таким
образом,
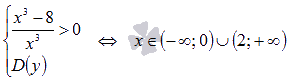 и
и
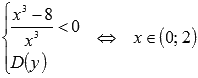 .
В
точке x = 2
функция определена и непрерывна, поэтому
ее следует добавить и к промежутку
возрастания и к промежутку убывания. В
точке x = 0
функция не определена, поэтому эту точку
не включаем в искомые интервалы.
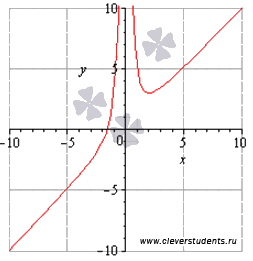
Приводим
график функции для сопоставления с ним
полученных результатов.
.
В
точке x = 2
функция определена и непрерывна, поэтому
ее следует добавить и к промежутку
возрастания и к промежутку убывания. В
точке x = 0
функция не определена, поэтому эту точку
не включаем в искомые интервалы.
Приводим
график функции для сопоставления с ним
полученных результатов.
 Ответ:
функция возрастает при
Ответ:
функция возрастает при
![]() ,
убывает на интервале (0;
2].
,
убывает на интервале (0;
2].
