11Уравнение касательной и нормали

Постановка задачи. Составить уравнение касательной и/или нормали к кривой   в точке с абсциссой .

План решения. Если функция  в точке  имеет конечную производную, то уравнение касательной имеет вид

, (1)

где  и .

Если , то уравнение касательной имеет вид .

Если , то уравнение нормали имеет вид

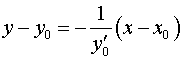. (2)

Если , то уравнение нормали имеет вид .

1. Находим значение .

2. Находим производную .

3. Подставляя найденные значения  и  в (1) и/или (2), получаем уравнения касательной и/или нормали.

Задача 2. Составить уравнение нормали к данной кривой в точке с абсциссой .

 

Уравнение нормали: .

Имеем:

.

, .

Получаем уравнение нормали:

 или .

 

Составить уравнение касательной к данной кривой в точке с абсциссой .

 

Уравнение касательной: .

Имеем:

.

, .

Получаем уравнение касательной:

 или .

УГОЛ МЕЖДУ ДВУМЯ КРИВЫМИ. Углом между двумя пересекающимися кривыми, лежащими в одной плоскости, назы­вается острый угол между каса­тельными к кривым в точке пере­сечения.

12. Производные высших порядков

Если функция дифференцируема при всех , то мы можем рассмотреть функцию , сопоставляющую каждой точке значение производной . Эта функция называется производной функции , или первой производной от . (Иногда саму исходную функцию называют нулевой производной и обозначают тогда .) Функция , в свою очередь, может иметь производную во всех (или некоторых) точках интервала , которую мы обозначим и назовём второй производной функции . Если предположить, что вторая производная существует во всех точках , то она может также иметь производную , называемую третьей производной функции , и т. д. Вообще, -й производной функции называется производная от предыдущей, -й производной :

если эта производная существует. -я производная называется также производной -го порядка, а её номер называется порядком производной.

При первую, вторую и третью производные принято обозначать штрихами: или ; при прочих  -- числом в скобках в верхнем индексе: или .

Физический смысл производной второго порядка проясняется из того, что если первая производная задаёт мгновенную скорость изменения значений в момент времени , то вторая производная, то есть производная от , задаёт мгновенную скорость изменения значений мгновенной скорости, то есть ускорение значений . Следовательно, третья производная -- это скорость изменения ускорения (или, что то же самое, ускорение изменения скорости, поскольку, как очевидно следует из определения, ).

Геометрический смысл второй производной связан с понятиями выпуклости и кривизны графика функции, и мы обсудим его ниже.

13. Дифференциалы высших порядков и их неинвариантность

Напомним, что дифференциал функции (называемый также первым дифференциалом, или дифференциалом первого порядка) задаётся формулой

Рассмотрим это выражение (при фиксированном приращении аргумента ) как функцию переменного и найдём её дифференциал :

Этот дифференциал от первого дифференциала называется вторым дифференциалом от функции , или дифференциалом второго порядка. Аналогично, дифференциал от второго дифференциала называется третьим дифференциалом; он задаётся формулой

Вообще, -й дифференциал , или дифференциал -го порядка, определяется как дифференциал от -го дифференциала (при постоянном приращении ); для него имеет место формула:

При -й дифференциал не инвариантен (в отличие от первого дифференциала), то есть выражение зависит, вообще говоря, от того, рассматривается ли переменная как независимая, либо как некоторая промежуточная функция другого переменного, например, .

Для доказательства неинвариантности дифференциалов высших порядков достаточно привести пример. Пусть и . Если  -- независимая переменная, то

(4.16)

Если же , то , и тогда правая часть формулы (4.16) даёт:

Однако при этом и

Как видно, получилось не то же самое, что по формуле (4.16) с учётом зависимости . Следовательно, уже второй дифференциал не обладает свойством инвариантности при замене переменной. Тем более, не инвариантны дифференциалы порядков 3 и выше.