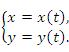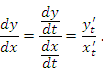6)Правила дифференцирования

 

Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

1) (с) ' = 0, (cu) ' = cu';

2) (u+v)' = u'+v';

3) (uv)' = u'v+v'u;

4) (u/v)' = (u'v-v'u)/v^2;

5) если y = f(u),

u = j(x), т.е. y = f((x)) - сложная функция, или суперпозиция, составленная из дифференцируемых функций  и f, то , или ;

6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем   ≠ 0, то .  

Дифференцирование сложных функций многих переменных

                Рассмотрим для простоты функцию двух переменных.

Теорема. Пусть u  = f (х, у) задана в области D и пусть х = х(t ) и у = у(t ) определены в области ,  причём, когда , то х и у принадлежат области D . Пусть функция u дифференцируема в  точке M₀ (x₀, y₀, z₀),  а функции х(t ) и у(t ) дифференцируемы в соответствующей точке t₀, то  сложная функция u = f [x(t), y(t)]=F (t) дифференцируема в точке t₀ и имеет место равенство:

.

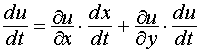Доказательство. Так как u дифференцируема по условию в точке (x₀, y₀), то её полное приращение представляется в виде

.

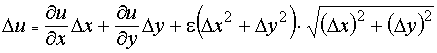                    Разделив это соотношение на , получим:

.

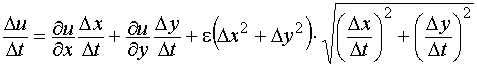                     Перейдём к пределу при и получим формулу

    .

Замечание 1. Если u = u(x, y) и x = x, y = y(x), то полная производная функции u по переменной х

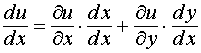или .

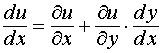Последнее равенство можно использовать для доказательства правила дифференцирования функции одной переменной, заданной неявно в виде F(x, y) = 0, где y = y(x) (см. тему № 3  и пример 14).

Имеем: 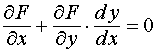. Отсюда 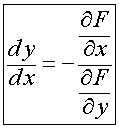.                  (6.1)

Вернёмся к примеру 14 темы № 3:

;

;

;

.

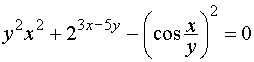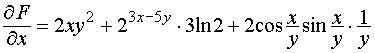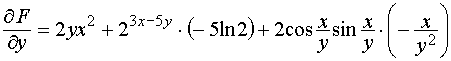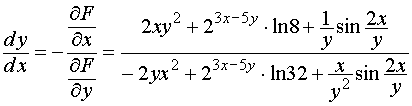Как видим, ответы совпали.

Замечание 2. Пусть u  = f (х, у), где х = х(t , v), у = у(t , v). Тогда u есть в конечном счёте сложная функция двух  переменных t и v . Если теперь функция u дифференцируема в точке M₀ (x₀, y₀), а функции х и у  дифференцируемы   в соответствующей точке (t₀, v₀), то можно говорить о частных производных по t и v от сложной функции в точке (t₀, v₀). Но если мы говорим о частной производной по t в указанной точке,  то вторая переменная v считается постоянной и равной v₀. Следовательно, речь идёт о производной только от сложной функции по t и, следовательно, мы можем воспользоваться выведенной формулой. Таким образом,   получим:

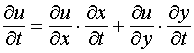и .

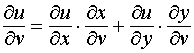Пример 13. Найти полную производную функции u = x ^y, где x = sin t, y = cos t .

.

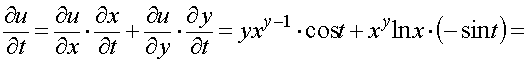
7.Логарифмическая производная

Логарифмическая произво́дная — производная от натурального логарифма функции.

Часто применяется для упрощения нахождения производной некоторых функции, например сложно-показательных.

Применение

Производная сложно-показательной функции

Пусть (для краткости , где u и g - функции).

Тогда , а . С другой стороны, , т.е. .

Окончательно имеем

Производная произведения функций

Пусть задана функция (для краткости ).

Так как .

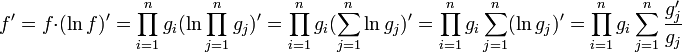Окончательно получаем: .

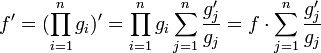Можно расписать формулу и прийти к другой форме:

Если , то

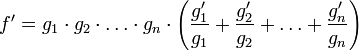
Раскрыв скобки, получим:

В частности, если 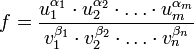, то

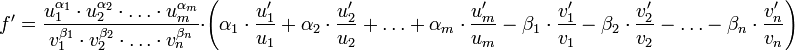
8. Производная неявно заданной функции.

Несомненно, в нашем сознании образ функции ассоциируется с равенством и соответствующей ему линией – графиком функции. Например, - функциональная зависимость, графиком которой является квадратичная парабола с вершиной в начале координат и направленными вверх ветвями; - функция синуса, известная своими волнами.

В этих примерах в левой части равенства находится y, а в правой части – выражение, зависящее от аргумента x. Другими словами, имеем уравнение, разрешенное относительно y. Представление функциональной зависимости в виде такого выражения называется явным заданием функции (или функцией в явном виде). И этот тип задания функции является для нас наиболее привычным. В большинстве примеров и задач нам предстают именно явные функции. Про дифференцирование функций одной переменной, заданных в явном виде, мы уже в деталях поговорили.

Однако, функция подразумевает соответствие между множеством значений величины x и множеством значений y, причем это соответствие НЕ обязательно устанавливается какой-либо формулой или аналитическим выражением. То есть, существует множество способов задания функции помимо привычного .

В данной статье мы рассмотрим неявные функции и способы нахождения их производных. В качестве примеров функций, заданных неявно, можно привести или .

Как Вы заметили, неявная функция определяется соотношением . Но не все такие соотношения между x и y задают функцию. Например, ни одна пара действительных чисел x и y не удовлетворяет равенству , следовательно, это соотношение неявную функцию не задает.

может неявно определять закон соответствия между величинами x и y, причем каждому значению аргумента x может соответствовать как одно (в этом случае имеем однозначную функцию) так и несколько значений функции (в этом случае функцию называют многозначной). К примеру, значению x = 1 соответствует два действительных значения y = 2 и y = -2 неявно заданной функции .

Неявную функцию привести к явному виду далеко не всегда возможно, иначе не пришлось бы дифференцировать сами неявные функции. Например, - не преобразовывается к явному виду, а - преобразовывается.

Теперь к делу.

Чтобы найти производную неявно заданной функции, необходимо продифференцировать обе части равенства по аргументу x, считая y – функцией от x, и после этого выразить .

Дифференцирование выражений, содержащих x и y(x), проводится с использованием правил дифференцирования и правила нахождения производной сложной функции. Давайте сразу подробно разберем несколько примеров, чтобы дальше не было вопросов.

9.Дифференцирование параметрически заданных функций

Пусть функция     задана параметрическими уравнениями где  t  – параметр.       Тогда производная этой функции по переменной  x  равна отношению производных     и     по параметру  t: Пример. Найти производную функции    , заданной уравнениями в параметрической форме:       Решение. Очевидно, что       Следовательно,