*4) Непрерывные функции Определения

Определение 1. Функция f(x) называется непрерывной в точке x0, если .

Дадим несколько расшифровок этого важнейшего определения.

а) Вспоминая понятие предела, запишем непрерывность f(x) в точке х0 в виде

б) Так как х₀=lim x, то непрерывность в точке х₀ можно записать в виде

Отсюда следует важнейшее свойство непрерывной функции: для непрерывной функции можно переставлять местами знак функции и знак предельного перехода

в) Обозначим x=x-x₀ (приращение аргумента) и f=f(x)-f(x₀) (приращение функции). Тогда непрерывность в точке х₀ означает, что , т.е. бесконечно-малому приращению аргумента соответствует бесконечно-малое приращение функции.

Введем обозначения:

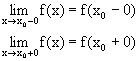
если эти пределы существуют.

Определение 2. Функция f(x) называется непрерывной в точке х₀ слева (справа) если f(x₀)=f(x₀ – 0) (f(x₀)=f(x₀+0)). Очевидно,что непрерывность в точке х₀ означает непрерывность слева и справа одновременно.

Определение 3. Функция f(x) называется непрерывной на некотором множестве Х, если она непрерывна в каждой точке этого множества, т.е. если

Обратите внимание, где стоит квантор , это важно.

Определение. Если функция f(x) не является непрерывной в точке х₀, то говорят, что в точке х₀ функция f(x) имеет разрыв.

Типы разрывов

А. Пусть существуют конечные f(x₀-0) и f(x₀+0), но они не равны друг другу . Тогда говорят, что в точке х₀функция f(x) имеет разрыв I рода или скачек.

График функции f(x) в окрестности точки х₀ имеет в этом случае примерно такой вид:

Величина |f(x₀+0)-f(x₀-0)| называется величиной скачка функции f(x) в точке х₀.

Б. Если хотя бы один из пределов бесконечен или не существует, то говорят, что в точке х₀ функция f(x) имеет разрыв второго рода.

Виды графика функции f(x) в окрестности точки х₀ в этом случае гораздо разнообразнее. Некоторые возможные варианты приведены ниже.

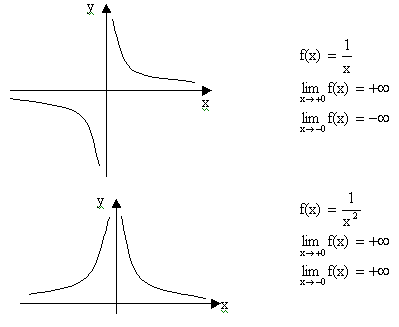
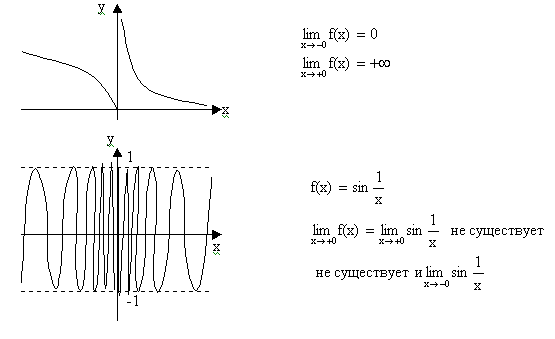
5)Производная, правила и формулы дифференцирования

Пусть функция y = f(x) определена в промежутке X. Производной функции y = f(x) в точке х _o называется предел

 = .

Если этот предел конечный, то функция f(x) называется дифференцируемой в точке x _o ; при этом она оказывается обязательно и непрерывной в этой точке.

Если же рассматриваемый предел равен ¥ (или - ), то при условии, что функция в точке х _o непрерывна, будем говорить, что функция f(x) имеет в точке х _o бесконечную производную.

Производная обозначается символами

y ,   f (x _o ),   ,   .

Нахождение производной называется дифференцированием функции. Геометрический смысл производной состоит в том ,ч то производная есть угловой коэффициент касательной к кривой y=f(x) в данной точке х _o ; физический смысл - в том, что производная от пути по времени есть мгновенная скорость движущейся точки при прямолинейном движении s = s(t) в момент t _o.

Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

1) (с) ' = 0, (cu) ' = cu';

2) (u+v)' = u'+v';

3) ( uv )' = u'v+v'u;

4) (u/v)' = (u'v-v'u)/v ^2;

5) если y = f(u), u = j (x), т.е. y = f( (x)) - сложная функция, или суперпозиция, составленная из дифференцируемых функций и f, то , или

;

6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем   0, то .

На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций.

1. (u ^)' = m u ^{m 1} u' ( Î R ).

2. ( a ^u )' = a ^u lna u'.

3. ( e ^u )' = e ^u u'.

4. (log _a u)' = u' /( u ln a).

5. (ln u)' = u'/u.

6. ( sin u)' = cos u u'.

7. (cos u)' = - sin u u'.

8. (tg u)' = 1/ cos ² u u'.

9. ( ctg u)' = - u' / sin ² u.

10. (arcsin u)' = u' / .

11. ( arccos u)' = - u' / .

12. (arctg u)' = u' /( 1 + u ² ).

13. (arcctg u)' = - u' /( 1 + u ² ).

Вычислим производную степенно-показательного выражения y=u ^v, (u>0), где u и v суть функции от х, имеющие в данной точке производные u', v'.

Прологарифмировав равенство y=u ^v, получим ln y = v ln u.

Приравнивая производные по х от обеих частей полученного равенства с помощью правил 3, 5 и формулы для производной логарифмической функции, будем иметь:

y'/y = vu'/u +v' ln u, откуда y' = y (vu'/u +v' ln u).

Итак ,

(u ^v )'=u ^v (vu'/u+v' ln u), u > 0.

Например, если y = x ^{sin x}, то y' = x ^{sin x} (sin x/x + cos x × ln x).

Если функция y = f(x) дифференцируема в точке x, т.е. имеет в этой точке конечную производную y', то  = y'+ , где 0 при х 0; отсюда y = y' х + x.

Главная часть приращения функции, линейная относительно х, называется дифференциалом функции и обозначается dy: dy = y' х. Если положить в этой формуле y=x, то получим dx = x' D х = 1 х = х, поэтому dy=y'dx, т. е. символ для обозначения производной  можно рассматривать как дробь.

Приращение функции D y есть приращение ординаты кривой, а дифференциал d y есть приращение ординаты касательной.

Пусть мы нашли для функции y=f(x) ее производную y = f (x). Производная от этой производной называется производной второго порядка функции f(x), или второй производной, и обозначается .

Аналогично определяются и обозначаются:

производная третьего порядка - ,

производная четвертого порядка -

и вообще производная n-го порядка - .