Теорема 6. Всякая элементарная функция непрерывна в каждой точке, в которой она определена. Первый замечательный предел

  Первым замечательным пределом называется предел отношения синуса бесконечно малой дуги к той же дуге, выраженной в радианной мере, при условии стремления этой дуги к нулю

.

  Непосредственное вычисление предела

приводит к неопределённости вида .    Из геометрических соображений имеем S_OAС< S_OAC < S_OBC. Используя формулы площадей рассматриваемых фигур, получим

или

sin x < x < tg x

Разделив все части неравенства на sin x > 0, получим при условии х > 0

,

или

.

Так как функция у = cos x непрерывна, то

.

Пользуясь теоремой о пределе промежуточной функции, получим окончательно

.

  Замечание. Если х < 0, то знаки неравенств изменяются на противоположные, выводы же остаются прежними.

Модификации первого замечательного предела

1. .

2. .

3. .

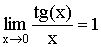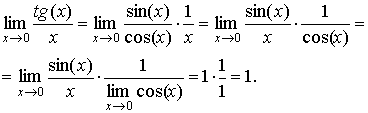
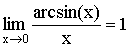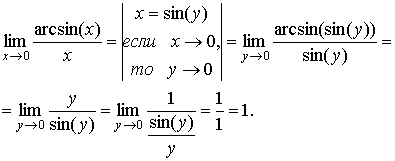
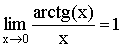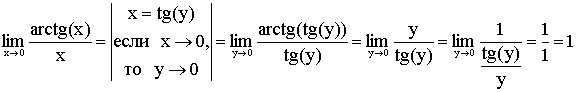
Второй замечательный предел

  Ранее для натурального n было доказано

.

  Докажем, что для любого действительного x имеет место так же равенство

.

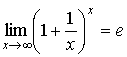  Доказательство. Для любого действительного положительного аргумента можно указать два последовательных натуральных числа, для которых будет выполнено неравенство n < x < n + 1. В том случае имеем n → ∞ ⇒ x → ∞. По свойству для неравенств имеем

.

Прибавим ко всем частям неравенств единицу

.

По свойству степеней имеем

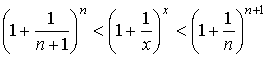
Так как

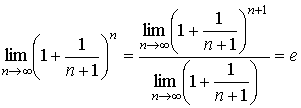
и

,

то по теореме о пределе промежуточной функции имеем также и

,

что и требовалось доказать. Для отрицательного х доказательство аналогично.

*3) Бесконечно малые величины

     1. Если переменная величина x_n имеет своим пределом нуль lim x_n = 0, то она называется бесконечно малой. Это же определение можно высказать и в другой формулировке:

     Переменная величина x_n назвается бесконечно малой, если для всякого наперед заданного положительного числа можно указать такое натуральное число N, что | x_n | < для всех номеров n, которые больше N.

     Ни одно число, кроме нуля, не может быть отнесено к бесконечно малым величинам.

     2. Алгебраическая сумма нескольких бесконечно малых величин есть также величина бесконечно малая.

     Алгебраической суммой называется такая сумма, члены которой присоединяются друг к другу не только при помощи знака плюс, но и при помощи знака минус.

     3. Разность двух бесконечно малых величин есть величина бесконечно малая.

     4. Произведение ограниченной переменной величины на бесконечно малую есть величина бесконечно малая.

     Отсюда следует:

     а) Произведение постоянной величины на бесконечно малую есть величина бесконечно малая.

     б) Произведение переменной величины, стремящейся к пределу, на бесконечно малую есть величина бесконечно малая.

     в) Произведение двух бесконечно малых величин есть величина бесконечно малая.

     5. Отношение двух бесконечно малых величин не обязательно есть величина бесконечно малая.

     Отношение двух бесконечно малых величин может быть величиной конечной, бесконечно малой и даже бесконечно большой величиной.

     Об отношении двух бесконечно малых величин иногда говорят, что оно представляет собой "неопределенность" вида .

     Вычисление предела отношения двух бесконечно малых часто называется также раскрытием "неопределенности" вида .

Сравнение бесконечно малых величин

Зададимся вопросом, как можно сравнить две бесконечно малые величины или две бесконечно большие величины?

Определения. Пусть при функции f(x) и g(x) являются бесконечно малыми. Тогда:

2. Если , то f(x) называется бесконечно малой высшего порядка относительно g(x).

2. Если (конечен и отличен от 0), то f(x) называется бесконечно малой n-го порядка относительно g(x).

3. Если , то f(x) и g(x) называются эквивалентными бесконечно малыми. Эквивалентность записывается так: .

Свойства эквивалентных бесконечно малых:

1. Разность двух эквивалентных бесконечно малых есть бесконечно малая высшего порядка относительно каждой из них.

2. Если из суммы нескольких бесконечно малых разных порядков отбросить бесконечно малые высших порядков, то оставшаяся часть, называемая главной, эквивалентна всей сумме.

Из первого свойства следует, что эквивалентные бесконечно малые могут сделаться приближенно равными со сколь угодно малой относительной погрешностью. Поэтому знак мы применяем как для обозначения эквивалентности бесконечно малых, так и для записи приближенного равенства их достаточно малых значений.