3. Базис системы векторов.

 Определение. Под системой векторов понимают несколько векторов, принадлежащих одному и тому же пространству R.

Замечание. Если система состоит из конечного числа векторов, то их обозначают одной и той же буквой с разными индексами.

Пример.

Определение. Любой вектор вида   =  называется линейной комбинацией векторов  . Числа   -коэффициентами линейной комбинации.

Пример.  .

Определение. Если вектор    является линейной комбинацией векторов  , то говорят, что вектор   линейно выражается через векторы  .

Определение. Система векторов называется линейно-независимой, если ни один вектор системы не может быть как линейная комбинация остальных векторов. В противном случае систему называют линейно-зависимой.

Пример. Система векторов   линейно-зависима, т. к. вектор  .

Определение базиса. Система векторов образует базис, если:

1) она линейно-независима,

2) любой вектор пространства через нее линейно выражается.

Пример 1. Базис пространства  :  .

 2. В системе векторов    базисом являются векторы:  , т.к.  линейно выражается через векторы  .

Замечание. Чтобы найти базис данной системы векторов необходимо:

1)     записать координаты векторов в матрицу,

2)    с помощью элементарных преобразований привести матрицу к треугольному виду,

3)     ненулевые строки матрицы будут являться базисом системы,

4)    количество векторов в базисе равно рангу матрицы. 

3.

Два вектора называются коллинеарными, если они лежат на одной и той же прямой или на параллельных прямых

Нуль-вектор считается коллинеарным любому вектору.

Условие коллинеарности двух векторов. Для того чтобы векторы a и b, заданные координатами, были коллинеарны, необходимо и достаточно, чтобы их координаты были пропорциональны. Т.е. существует такое действительное число λ, что

x₁ = λ x₂,

y₁ = λ y₂,

z₁ = λ z₂

Условие перпендикулярности двух векторов. Для того чтобы векторы a и b были перпендикулярны, необходимо и достаточно, чтобы их склярное произведение было равно нулю.

4.

Скалярное произведение векторов

Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

Скалярное произведение векторов  ,   обозначается символом   (порядок записи сомножителей безразличен, то есть  ).

Если угол между векторами  ,   обозначить через  , то их скалярное произведение можно выразить формулой

 (1)

Скалярное произведение векторов  ,   можно выразить также формулой

, или  .

Из формулы (1) следует, что  , если   - острый угол,  , если   - тупой угол;   в том и только в том случае, когда векторы   и   перпендикулярны (в частности,  , если   или  ).

Скалярное произведение   называется скалярным квадратом вектора и обозначается символом  . Из формулы (1) следует, что скалярный квадрат вектора равен квадрату его модуля:

.

Если векторы   и   заданы своими координатами:

,  ,

то их скалярное произведение может быть вычислено по формуле

.

Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов

.

Угол   между векторами

,  ,

дается формулой 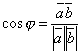 , или в координатах

.

Проекция произвольного вектора   на какую-нибудь ось u определяется формулой

,

где   - единичный вектор, направленный по оси u. Если даны углы  ,  ,  , которые оси u составляет с координатными осями, то   и для вычисления вектора   может служить формула

.

5.