Квазистатическая самофокусировка

Такой процесс происходит при длительности импульса гораздо больше времени установления нелинейности: _о>>_нл.

Таким образом, если перейти к бегущей системе координат: z=z, , и пренебречь дисперсионным расплыванием, то для каждого момента времени справедливо уравнение (73), т.е. время входит как параметр. Поэтому решение уравнения (73) аналогично, то появляется зависимость от :

длина самофокусировки Lсф становится функцией времени – возникает движение фокальной точки.

На рисунке приведена квазистатическая картина движения фокальной точки самофокусирующегося пучка:

Лазерный импульс поступает в АС. Сначала, т.к. P(t)<Pкр, происходит уменьшеие расходимости пучка, но не го самофокусировка. Как только P(t)>Pкр, то образуется фокальная точка, т.е. пучок саомфокусируется. Далее мощность импульса P(t) возрастает и, соответственно, Lсф уменьшается, фокальная точка перемещается так, чтобы уменьшить длину самофокусировки. Это продолжается, пока мощность импульса не достигнет максимума, после этого фокальная длина возрастает, пока P₀(t) снова не станет меньше Pкр (см. зависимость Lсф()).

Каждая точка огибающей P₀(t) фокусируется в своё определённое время и на своём определённом расстоянии z. В итоге, т.к. различающихся точки огибающей P₀(t) много, то получается картина движения фокуса z(t) при самофокусировке лазерного импульса.

При квазистатической фокусировке одномодового (поперчные моды) лазерного импульса положение фокуса перемещается в соответствии с мгновенным значением мощности P₀(t). Т.к. при УКИ не возможно напрямую измерить длительность импульса, то и движение фокуса напрямую невозможно отследить, поэтому на фотографиях это перемещение видно в качестве нити. При фокусировке многомодового импульса, имеющего сложное распределение интенсивности в поперечном сечении, происходит разбиение пучка на несколько независимых самофокуирующихся частей, каждая из которых образует нить.

Нестационарная самофокусировка

При длительности импульса _о, сравнимых с _нл (или _о<_нл), помимо волнового уравнения, описывающего распространение излучения в среде, необходимо совместно решить и динамические уравнения, описывающие нелинейный отклик среды.

Самовоздействие переднего фронта и хвоста импульса при нестационарной самофокусировке существенно различаются. На временах t<<_нл нелинейный отклик не успевает установиться, поэтому передний фронт распространяется так же, как и в линейной среде. В то время, как хвост импульса может сильно самофокусироваться. Качественная картина нестационарного самофокусирования:

Части а, б дифрагируют как в линейной среде, для соответствующих им моментов времени <<_нл значение n (нелинейной добавки к показателю преломления) чрезвычайно мала и самофокусировка отсутствует. Для частей в-д величина n достаточна, чтобы привести к самофокусировке. В результате пучок трансформируется, приобретает форму рупора.

Пример процесса самофокусировки.

В качестве примера рассмотрим реальный процесс самофокусировки коротких ФС – лазерных импульсов в кварцевом стекле.

Пример получим на основе численных решений уравнения непосредственно следующего из уравнений Максвелла.

При численном решении считалось:

- Пространственная и временная форма лазерного импульса имеет вид функции Гаусса:

(78)

,где

- При столь короткой длительности импульса

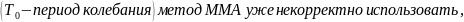
поэтому решение получено для E – напряженности электрического поля, а не для А- комплексной амплитуды поля, как для метода ММА.

сапфирового лазера.

много модового волокна.

- Для учета дисперсии, зависимость n(ω) имела полиномиальный вид:

где ,a,b –эмпирические константы для кварцевого стекла:

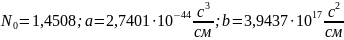
Таким образом, данная зависимость n(ω) позволяет учитывать дисперсию 3-его и более высоких порядков. При длине волны дисперсия для кварцевого стекла нормальная, нелинейная добавка по интенсивности , нелинейный отклик среды квазистатический.

На следующих 3-ех рисунках (рис.16-18) представлены результаты численного решения для 3-ех различных пиковых значений интенсивности. На рисунках представлены зависимости нормированной напряженности электрического поля от поперечной координаты r и времени η в бегущей системе координат для различного пройденного расстояния z в кварцевом стекле.

Рисунки слева – это 3-ех мерное распределение , поскольку часть импульса, характеризуемая отрицательными значениями поля, симметрична положительным значениям, то показаны только положительные значения поля. На рисунках справа приведены те же данные, что и слева, но в 2-х мерной проекции, светло-серые части изображения соответствуют положительным значениям поля, темно-серые – отрицательным значениям.

На рисунке 16 приведена трансформация поля E(z,r,η) с пиковой исходной интенсивностью

Из рисунка видно, что данной интенсивности импульса не хватает для достаточно заметных нелинейных эффектов. Импульс при распространении претерпевает дифракционное пространственное уширение и дисперсионное расплывание. При этом в соответствии с дисперсией в нормальной среде импульс приобретает “+” чирп, т.е. частота колебаний растет к хвосту импульса. Эффекты, связанные с дисперсией 3-его порядка не наблюдаются.

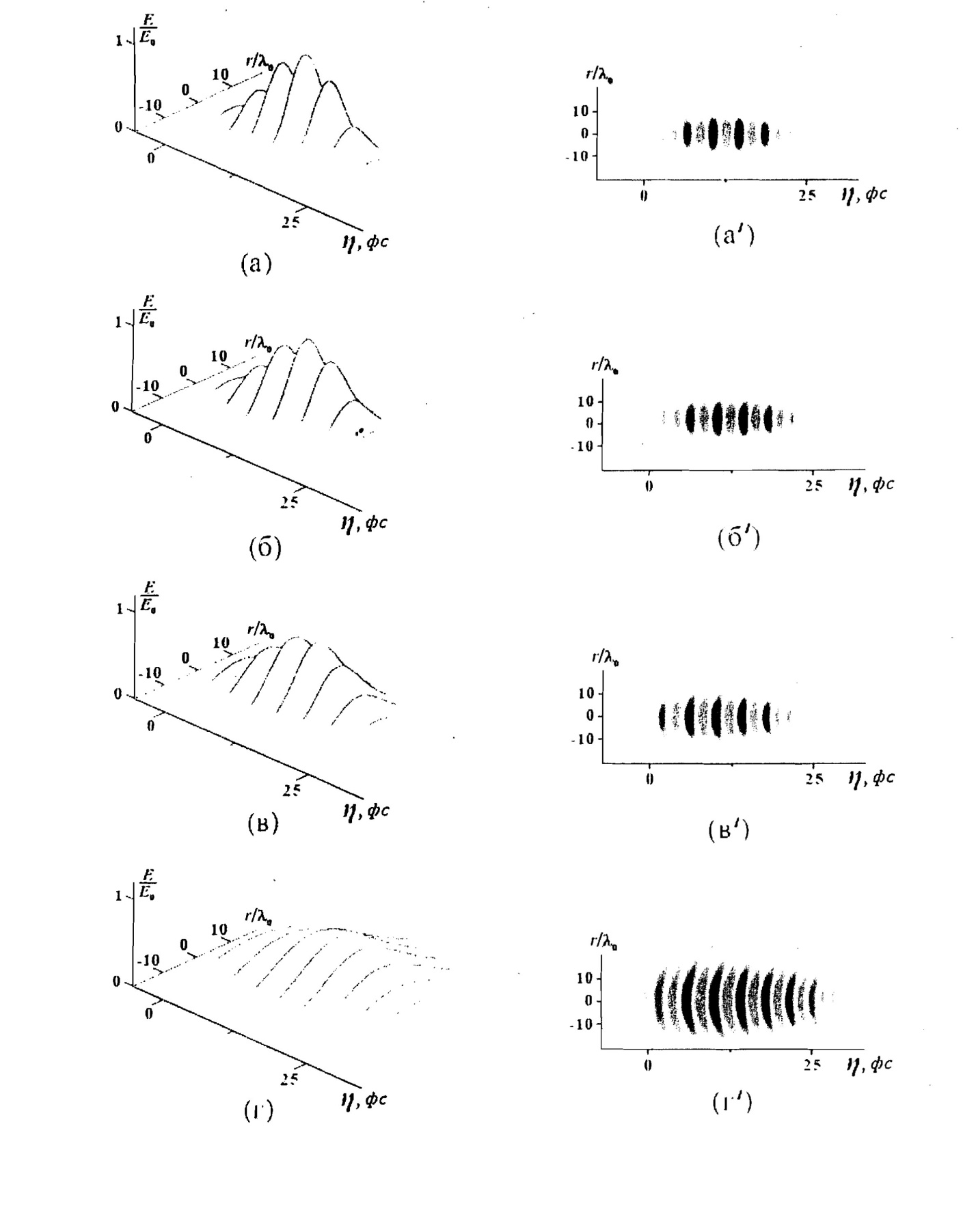
Пространственно-временная эволюция электрического поля ФС-импульса в кварцевом стекле.

а-а’)z=0 мм , б-б’)z=0.1 мм, в-в’)z=0.2 мм, г-г’)z=0.4мм.

Рис.16

Пространственно-временная эволюция электрического поля ФС-импульса в кварцевом стекле.

а-а’)z=0 мм , б-б’)z=0.1 мм, в-в’)z=0.2 мм, г-г’)z=0.4мм.

Рис.17

-форма импульса сокращается из (Г’) видно, что в следствии зависимости n(I),поперечные области импульса приобретают дополнительный фазовый набег- соответственно волновой фронт искривляется и имеет вогнутый характер.

На рисунке17 приведены трансформации поля E(z,r, ) с пиковой сходной интенсивностью I=1.5 x 10^13 вт/см^2.

Из рисунка видно, что при какой интенсивности нелинейные эффекты существенны.

Из а’- в’ видно проявление эффекта квазистатической самофокусировки - поперечный размер импульса уменьшается. Т.к значение интенсивности в разных поперечных сечениях различно, то и сократить самофокусировка тоже различна - центральная часть импульса обладает большей I и соответственно быстрее самофокусируется.

В итоге импульс приобретает форму “гантели” дальнейшее “разбухание” импульса (Г’) обусловлено дисперсионным расплыванием-по временной оси, дифракцией и прохождением плоскости фокусировки - по пространственной оси.

На рисунке 18 приведены трансформация поля E(z,r, ) c пиковой входной интенсивностью I=2.5 X 10^13 вт/см^2.

На первой стадии, как и в случае, рассмотренном выше, самофокусировка обеспечивает увеличения поля в приосевой части пучка. При этом из (б’) видно, что область фокусировки смещается к задней части импулса и поперечный размер импульса гораздо меньше чем при I=1.5 x 10^13 вт/см^2.

В случае, поперечный размер светового канала становится соизмерим с длиной волны, начинают сказываться нелинейные эффекты, не играющие роли при прохождении «фокальной» плоскости импульса, при движении также “разбухание”(г‘). Разбухание происходит не симметрично, в центральной части импульса образуется ”пузырь” в котором значение E мало.

1) уменьшение поперечного размера ведет к увеличению I ,что в свою очередь увеличивает скорость самофокусировки.

Смещения области фокусировки к хвосту импульса и образование светового “пузыря” можно объяснить явлением, которое называется ударной волной огибающей.