2. Статистична ймовірність

Нехай А – випадкова подія, пов’язана з деяким дослідом. Повторимо дослід п разів за одних і тих же умов, і нехай при цьому подія А з’явилась т разів.

Відношення числа дослідів, в яких подія А з’явилась до загального числа п проведених дослідів, називається частотою події А

.

Частоту можна знайти тільки після проведення випробувань. У багатьох випадках відносна частота події А стабілізується при великому п. Такі події називаються статистично стійкими.

Приклад 1.7. Відділ технічного контролю виявив 5 бракованих книг у партії з випадково відібраних 100 книг. Знайти відносну частоту появи бракованих книг.

Розв’язання: ; . Маємо .

3. Геометрична ймовірність

Нехай Ω – деяка область на прямій, площині або в просторі, А – деяка частина області Ω. В області Ω навмання вибирають точку, вважаючи, що вибір точок області рівноможливий. Ймовірність того, що вибрана точка належить А, визначається рівністю

(1.5)

де – міра (довжина, площа, об’єм) А, Ω.

Приклад 1.8. Статутний фонд банку – а грош. од. – був випадковим чином поділений на три частини, в результаті чого створено три нові банки. Знайти ймовірність того, що жоден із банків не припинить свого існування, якщо для їх роботи необхідний статутний фонд не менше, ніж 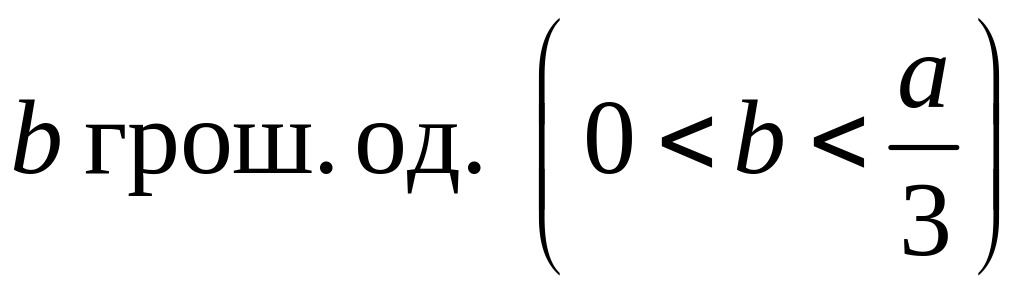. Обчислити при грош. од; грош. од.

Розв’язання. Нехай х – статутний фонд 1-го банку, у – уставний фонд 2-го банку, тоді – статутний фонд 3-го банку. Під випадковим поділом відрізка на три частини розумітимемо його поділ двома точками, кожна з яких має на даному відрізку рівномірний розподіл.

Область можливих наслідків

Область сприятливих наслідків

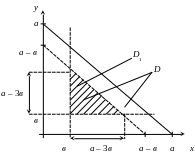
Рис. 1.1. Геометричне зображення простору і події до прикладу 1.8

Площа області площа області

Шукана ймовірність . З останньої формули видно, що чим менший статутний фонд а, тим менша ймовірність того, що нові банки не припинять свого існування.

При грош. од., грош. од. маємо

Питання для самоконтролю

1. Дати означення класичної ймовірності (навести приклади).

2. Сформулювати властивості ймовірності.

3. Дати означення статистичної ймовірності (навести приклади).

4. Дати означення геометричної ймовірності (навести приклади).

Вправи

1. В урні 100 куль, позначених номерами 1, 2, 3, …, 100. Із урни навмання вийнято одну кулю. Яка ймовірність того, що номер вийнятої кулі:

а) містить цифру 5;

б) є однозначним?

2. В одній урні знаходяться кулі з номерами 1, 2, 3, 4, 5, а в другій – з номерами 6, 7, 8, 9, 10. З кожної урни вийнято по одній кулі. Яка ймовірність того, що сума номерів вийнятих куль:

а) дорівнює 11;

б) не менша 7?

3. З букв розрізної абетки складено слово “функція”. Букви розсипали, а потім склали в довільному порядку. Яка ймовірність того, що знову отримали слово “функція”?

4. При наборі телефонного номера абонент забув дві останні цифри і набрав їх навмання, пам’ятаючи тільки, що ці цифри непарні та різні. Знайти ймовірність того, що номер набраний правильно.

5. Президент фірми хоче створити команду дизайнерів для розробки нової моделі товару у складі трьох інженерів і двох спеціалістів з дослідження ринку. Яка ймовірність, що група такого складу буде створена, якщо з групи 10 інженерів і 5 спеціалістів з проблем ринку потрібно вибрати п’ять осіб?

6. Знайти ймовірність того, що навмання вибране з чисел від 9 до 100 ділиться на 4.

7. Замок містить 4 диски, на кожному з яких 10 цифр. Замок відімкнеться, якщо правильно набрано код із чотирьох цифр. Яка ймовірність того, що замок відімкнуть з першої спроби?

8. У пачці є 100 лотерейних білетів, один з яких виграшний. Яка ймовірність виграти, якщо купили 10 білетів?

9. До білета іспиту входять 4 питання із 45, що містить програма. Студент вивчив 30 питань. Яка ймовірність того, що він буде знатиме всі 4 питання з навмання взятого білета?

10. Слово “інтеграл” складається з букв розрізної азбуки. Навмання, одна за одною, дістали 3 картки і розклали в ряд у порядку появи. Яка ймовірність того, що:

а) вийшло слово “гра”;

б) з відібраних карток можна скласти слова “гра”?

11. З 10 книг, що стоять на книжковій полиці, – 3 книги із статистики. Знайти ймовірність того, що вони стоять поруч.

12. На книжковій полиці випадковим чином розставляють 4 книги з економіки і три книги з географії. Яка ймовірність того, що книги з одного предмета стоятимуть поруч?

13. На книжковій полиці розставили 6 томів енциклопедії. Яка ймовірність того, що:

а) томи 1 і 2 розміщено поруч;

б) томи 3 і 4 не поставлено поруч?

14. Статутний фонд банку в а грош. од. був випадковим чином поділений на три частини, в результаті чого створено три нові банки. Знайти ймовірність того, що жоден із банків не припинить свого існування, якщо для роботи банку необхідний статутний фонд не менше, ніж в . Обчислити Р при грош. од.;

15. При стрілянні з гвинтівки відносна частота попадання в ціль виявилась 0,85. Знайти число влучень, якщо було зроблено 120 пострілів?

16. У прямокутному трикутнику з катетами довжиною 3 і 4 м навмання вибрали точку. Яка ймовірність того, що вона потрапить у круг, вписаний у трикутник?

17. У круг вписано квадрат. Яка ймовірність того, що навмання вибрана точка круга потрапить у квадрат?

18. Знайти ймовірність того, що навмання вибрана точка правильного трикутника потрапляє в коло, вписане в цей трикутник?

19. Яка ймовірність, що навмання вибрана точка правильного трикутника потрапить у вписаний у трикутник квадрат?