3.10.5. Перевірка гіпотези про рівність дисперсій двох незалежних випадкових величин

Перевіряти гіпотезу про рівність двох дисперсій доводиться досить часто, наприклад, під час аналізу стабільності виробничого процесу до і після введення нової технології (коливання у випуску продукції вимірюється за допомогою квадратичного відхилення), вивчення якості вимірювальних приладів (порівняння дисперсій показників окремих приладів), вивчення ступеня однорідності двох сукупностей щодо деякої ознаки (кваліфікації працівників, стажу персоналу тощо). Потреба перевірити рівність дисперсій виникає і під час порівняння середніх величин сукупностей.

Отже, припустимо, що випадкові величини та Y, що характеризують дві статистичні сукупності, незалежні, нормально розподілені з невідомими дисперсіями і відповідно.

Перевіримо гіпотезу про рівність дисперсій випадкових величин X і Y.

Вважають відомими:

1) дані двох незалежних вибірок обсягів і для випадкових величин X і Y відповідно;

2) рівень значущості

Критерій перевірки гіпотези базується на зіставленні виправлених вибіркових дисперсій і , обчислених за даними вибірок. Так, у припущеннях даної моделі випадкова величина

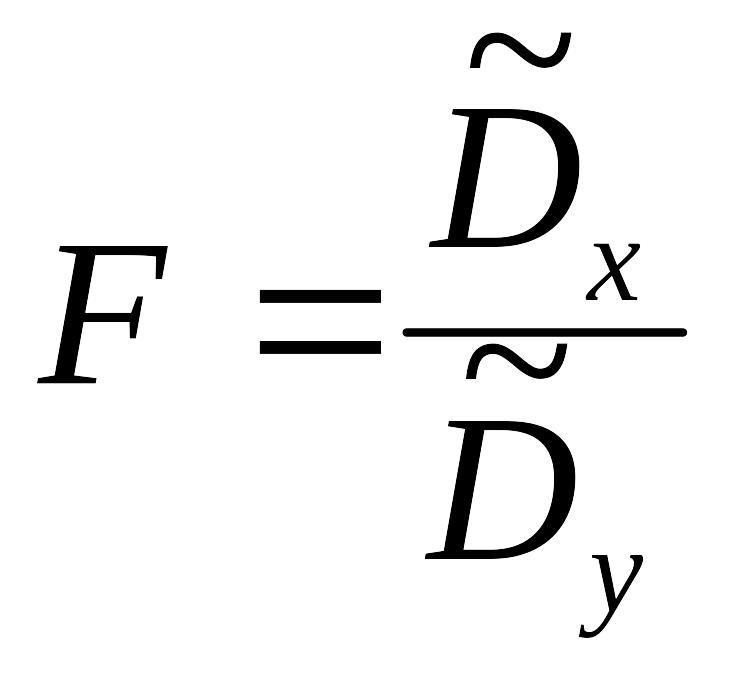, (3.48)

за умови виконання гіпотези розподілена за законом Фішера-Снедекора з і ступенями вільності.

Правило. Якщо нульова гіпотеза , а конкуруюча , то перевірку гіпотези здійснюємо за схемою:

1) знаходимо емпіричне значення критерію за формулою (3.48);

2) за таблицею критичних точок розподілу Фішера-Снедекора для заданого рівня значущості і ступенів вільності і знаходимо критичну точку правосторонньої області (додаток Д);

3) робимо висновок щодо прийняття гіпотези H₀:

а) якщо то гіпотезу H₀ приймаємо;

б) якщо то гіпотезу відхиляємо на користь альтернативної гіпотези

У випадку, коли критерій узгодження і

Зауваження. Якщо нульова гіпотеза а конкуруюча то перевірку гіпотези здійснюємо за сформульованим правилом, в якому змінюється лише методика знаходження критичного значення а саме: із таблиці критичних точок розподілу Фішера-Снедекора критичну точку визначаємо за рівнем значущості удвічі меншого від заданого, і ступенів вільності і (див. додаток Д).

Приклад 3.16. Дані дві незалежні вибірки обсягом і що отримані з генеральних сукупностей та , що розподілені за нормальним законом. Знайдені виправлені вибіркові дисперсії та , Перевіримо при рівні значущості нульову гіпотезу про рівність генеральних дисперсій при конкуруючій гіпотезі

Розв’язання. Знайдемо значення (див. додаток Д). Критична область – правостороння. Обчислимо значення критерію, що спостерігається, 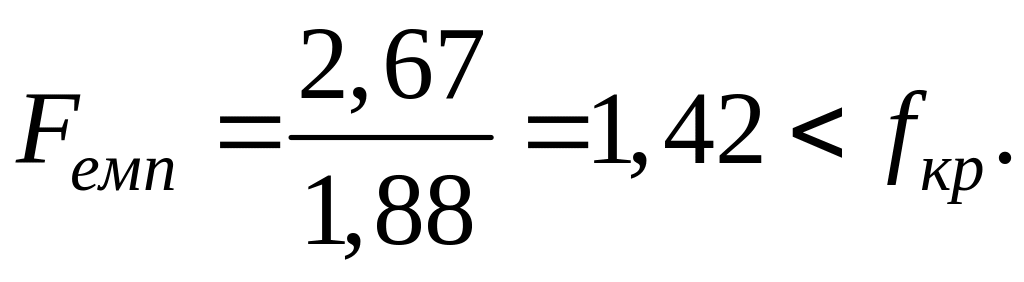Отже, немає підстав відхилити нульову гіпотезу.

3.10.6. Перевірка гіпотези про значущість коефіцієнта кореляції

Припустимо, що двовимірна генеральна сукупність розподілена нормально. Із цієї сукупності отримали вибірку обсягу n, за цією вибіркою знайдено коефіцієнт кореляції який є відмінним від нуля. Оскільки вибірка випадкова, то ще не можна зробити висновок, що коефіцієнт генеральної сукупності також відмінний від нуля. Врешті-решт нас цікавить саме цей коефіцієнт, тому виникає необхідність при заданому рівні значущості перевірити нульову гіпотезу про рівність нулю генерального коефіцієнта кореляції при конкуруючій

Якщо нульова гіпотеза відхиляється, то це означає, що вибірковий коефіцієнт кореляції значно відрізняється від нуля (є значущим), а та – корельовані.

Якщо нульова гіпотеза приймається, то вибірковий коефіцієнт кореляції незначущий, а та – корельовані.

За критерій перевірки нульової гіпотези приймемо випадкову величину:

Величина T при справедливості нульової гіпотези має розподіл Стьюдента з ступенями вільності.

Оскільки конкуруюча гіпотеза то критична область – двостороння, яка будується виходячи з вимоги, щоб імовірність попадання критерію T у цю область у припущенні справедливості нульової гіпотези дорівнювала прийнятому рівню значущості

Правило. Для того, щоб при заданому рівні значущості перевірити нульову гіпотезу про рівність нулю генерального коефіцієнта кореляції нормальної двовимірної випадкової величини при конкуруючій гіпотезі необхідно:

1) обчислити значення критерію, що спостерігається:

(3.49)

2) за таблицею критичних точок розподілу Стьюдента за даним рівнем значущості та ступенями вільності знайти критичну точку для двосторонньої критичної області (див. додаток Г);

3) робимо висновок стосовно висунутої гіпотези:

а) якщо то немає підстав відхилити гіпотезу

б) якщо то відхиляємо гіпотезу на користь альтернативної.

Приклад 3.17. За вибіркою обсягу , що отримана з нормально розподіленої двовимірної генеральної сукупності, обчислено вибірковий коефіцієнт кореляції Перевіримо при рівні значущості нульову гіпотезу про рівність нулю генерального коефіцієнта кореляції при конкуруючій гіпотезі

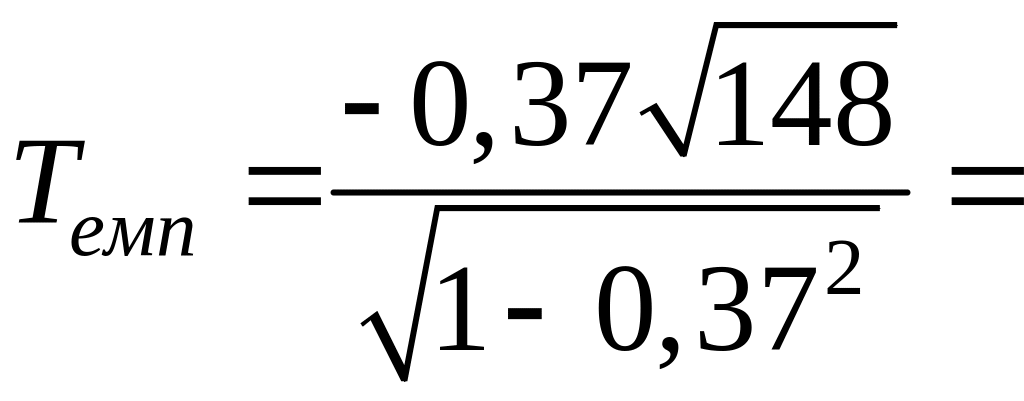
Розв’язання. Критична точка (див. додаток Г). Обчислимо значення критерію, що спостерігається: Оскільки |, то нульова гіпотеза відхиляється, тобто та корельовані.