
- •Т.І. Малютіна, к.А. Дахер вища математика для економістів
- •Теорія ймовірностей і математична статистика
- •Розділ і випадкові події
- •1.1. Простір елементарних подій. Випадкові події та операції над ними. Комбінаторика
- •1.1.1. Основні поняття теорії ймовірностей. Операції над подіями
- •Питання для самоконтролю
- •1.1.2. Елементи комбінаторики
- •Розв’язування комбінаторних задач
- •Питання для самоконтролю
- •1.2. Ймовірність випадкової події. Способи обчислення ймовірностей випадкових подій
- •1. Класичне означення ймовірності
- •2. Статистична ймовірність
- •3. Геометрична ймовірність
- •Питання для самоконтролю
- •1.3. Теореми додавання і множення ймовірностей. Умовна ймовірність
- •Питання для самоконтролю
- •1.4. Формула повної ймовірності. Формула Байєса
- •Питання для самоконтролю
- •1.5. Послідовні незалежні випробування
- •1.5.1. Формула Бернуллі
- •1.5.2. Формула Пуассона
- •1.5.3. Локальна теорема Муавра-Лапласа
- •1.5.4. Інтегральна теорема Муавра-Лапласа
- •Питання для самоконтролю
- •Розділ іі випадкові величини
- •2.1. Одновимірні випадкові величини. Способи задання
- •2.1.1. Дискретні випадкові величини. Функція розподілу. Основні закони розподілу
- •2.1.2. Неперервні випадкові величини. Щільність розподілу. Основні закони розподілу
- •Питання для самоконтролю
- •2.2. Числові характеристики випадкових величин
- •1. Математичне сподівання
- •2. Дисперсія та середнє квадратичне відхилення
- •3. Початкові та центральні моменти
- •4. Мода і медіана
- •Числові характеристики деяких розподілів
- •Питання для самоконтролю
- •2.3. Рівномірний, показниковий, нормальний розподіли
- •Питання для самоконтролю
- •2.4. Граничні теореми теорії ймовірностей. Закон великих чисел і центральна гранична теорема. Нерівність ЧебишОва
- •2.4.1. Лема Чебишова
- •2.4.2. Теорема Чебишова
- •2.4.3. Теорема Бернуллі
- •Питання для самоконтролю
- •2.5. Двовимірна випадкова величина
- •2.5.1. Закон розподілу ймовірностей. Закони розподілу компонент
- •2.5.2. Функція розподілу двовимірної випадкової величини та її властивості
- •2.5.3. Щільність сумісного розподілу ймовірностей неперервної двовимірної випадкової величини, основні властивості. Ймовірність попадання випадкової точки в задану область
- •2.5.4. Умовні закони розподілу складових системи дискретних і неперервних випадкових величин. Залежні та незалежні випадкові величини
- •1. Випадок дискретної величини
- •2. Випадок неперервної величини
- •Питання для самоконтролю
- •2.5.5. Числові характеристики двовимірної випадкової величини. Кореляційний момент і коефіцієнт кореляції
- •Числові характеристики двовимірної випадкової величини
- •Питання для самоконтролю
- •2.5.6. Умовні числові характеристики двовимірної випадкової величини. Регресія
- •1. Випадок дискретної випадкової величини
- •2. Випадок неперервної випадкової величини
- •Питання для самоконтролю
- •Розділ III елементи математичної статистики
- •3.1. Предмет та основні завдання математичної статистики
- •3.2. Генеральна та вибіркова сукупності. Вибірка. Способи відбору
- •Питання для самоконтролю
- •3.3. Статистичний розподіл вибірки
- •Питання для самоконтролю
- •3.4. Графічне зображення статистичних розподілів
- •3.5. Емпірична функція розподілу. Кумулята
- •Питання для самоконтролю
- •3.6. Числові характеристики статистичного розподілу вибірки
- •Питання для самоконтролю
- •3.7. Статистичні оцінки параметрів генеральної сукупності
- •3.7.1. Статистичні оцінки невідомих параметрів розподілу та їх властивості
- •3.7.2. Статистична оцінка математичного сподівання
- •3.7.3. Статистична оцінка дисперсії. Виправлена дисперсія
- •3.7.4. Метод моментів статистичного оцінювання параметрів розподілу
- •3.7.5. Метод максимуму правдоподібності статистичного оцінювання параметрів розподілу
- •Питання для самоконтролю
- •3.8. Інтервальні оцінки параметрів розподілу
- •3.8.1. Надійність. Інтервал довіри
- •3.8.2. Розподіл – “хі-квадрат”
- •3.8.3. Розподіл Стьюдента
- •3.8.4. Розподіл Фішера-Снедекора
- •3.8.5. Інтервальні оцінки для математичного сподівання
- •3.8.6. Оцінка істинного значення вимірюваної величини
- •3.8.7. Інтервали довіри для середнього квадратичного відхилення нормально розподіленої випадкової величини
- •3.8.8. Оцінка точності вимірювань
- •Питання для самоконтролю
- •3.9. Елементи теорії кореляції
- •3.9.1. Функціональна, статистична й кореляційна залежності
- •3.9.2. Вибірковий коефіцієнт кореляції. Коефіцієнт детермінації
- •Питання для самоконтролю
- •3.9.3. Основні поняття і методи регресійного аналізу
- •3.9.4. Метод найменших квадратів
- •Питання для самоконтролю
- •3.10. Статистична перевірка статистичних гіпотез
- •3.10.1. Статистичні гіпотези. Помилки першого та другого роду
- •3.10.2. Статистичний критерій перевірки нульової гіпотези
- •Питання для самоконтролю
- •3.10.3. Перевірка гіпотези про закон розподілу. Критерій згоди Пірсона
- •3.10.4. Перевірка гіпотези про порівняння середнього значення ознаки генеральної сукупності зі стандартом
- •3.10.5. Перевірка гіпотези про рівність дисперсій двох незалежних випадкових величин
- •3.10.6. Перевірка гіпотези про значущість коефіцієнта кореляції
- •Питання для самоконтролю
- •Список використаної та рекомендованої літератури
- •Додаток а
- •Додаток б
- •Додаток в
- •Додаток г
- •Додаток д Критичні точки розподілу f Фішера-Снедекора
- •Додаток е
- •Додаток ж Значення
- •Вища математика для економістів
- •40030, М. Суми, вул. Петропавлівська, 57
3.7.5. Метод максимуму правдоподібності статистичного оцінювання параметрів розподілу
На підставі даних
вибірки
![]() отриманої внаслідок спостережень над
випадковою величиною X, потрібно
оцінити невідомий параметр
отриманої внаслідок спостережень над
випадковою величиною X, потрібно
оцінити невідомий параметр
![]() Припустимо, що закон розподілу випадкової
величини
відомий із точністю до параметра
і визначається за допомогою функції
Припустимо, що закон розподілу випадкової
величини
відомий із точністю до параметра
і визначається за допомогою функції
![]() яка у випадку дискретної випадкової
величини X задає ймовірність події
яка у випадку дискретної випадкової
величини X задає ймовірність події
![]() а у випадку неперервної випадкової
величини
– щільність її розподілу.
а у випадку неперервної випадкової
величини
– щільність її розподілу.
Функцією правдоподібності називають функцію
![]()
яка зображує сумісний розподіл випадкового вектора з незалежними компонентами, кожна з яких має той самий розподіл, що й випадкова величина X.
Ідея
методу максимуму правдоподібності:
за статистичну оцінку невідомого
параметра
приймають таке його значення
![]() для якого функція правдоподібності
для якого функція правдоподібності
![]() що розглядається як функція від
при фіксованих значеннях
досягає максимуму.
що розглядається як функція від
при фіксованих значеннях
досягає максимуму.
Схема статистичного оцінювання параметра методом максимуму правдоподібності:
1) досліджуємо
функцію правдоподібності
![]() на максимум за допомогою методів
диференціального числення: знаходимо
критичні точки
на максимум за допомогою методів
диференціального числення: знаходимо
критичні точки
![]() із системи рівнянь:
із системи рівнянь:
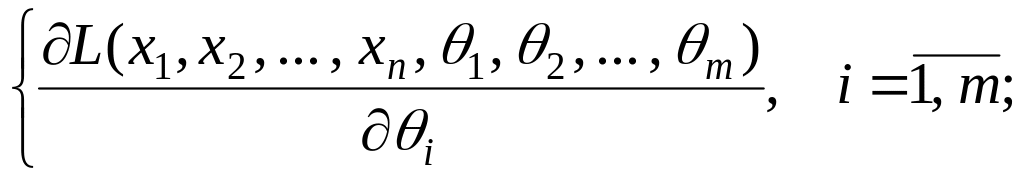
Для
спрощення обчислень зручно замість
функції
![]() розглядати
логарифмічну
функцію правдоподібності
розглядати
логарифмічну
функцію правдоподібності
![]() оскільки точки екстремуму для функцій
оскільки точки екстремуму для функцій
![]() і
і
![]() збігаються, бо
збігаються, бо
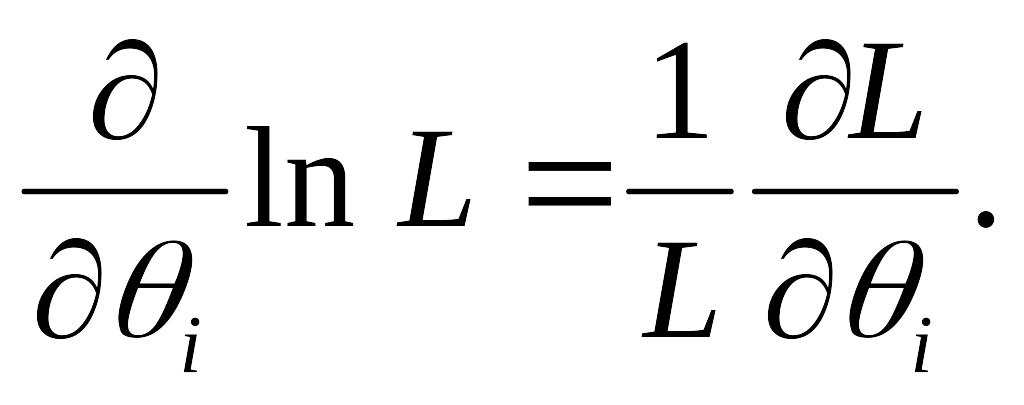 Знаходимо критичні точки функції
із системи рівнянь:
Знаходимо критичні точки функції
із системи рівнянь:
![]()
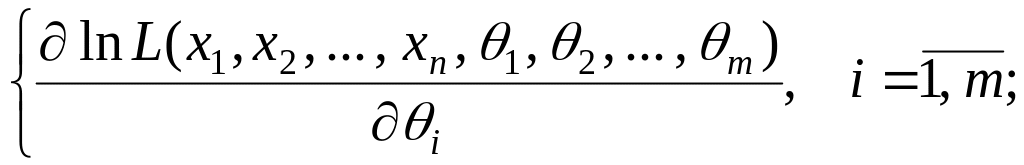
розв’язки
якої
![]()
2) використовуючи достатні умови екстремуму функції, знаходимо точку максимуму.
Метод максимуму правдоподібності статистичного оцінювання параметрів розподілу має низку важливих переваг:
вони слушні, асимптотично нормально розподілені (при великому обсязі вибірки їх розподіл близький до нормального) і мають найменшу дисперсію в порівнянні з іншими асимптотично нормальними оцінками;
найбільш повно використовуються дані вибірки для оцінки параметрів, тому цей метод особливо корисний за малих обсягів вибірки.
Недолік методу в тому, що він часто вимагає складних обчислень.
Найчастіше цей метод використовується при біноміальному, показниковому розподілах і розподілі Пуассона.
У випадку
біноміального розподілу функція
правдоподібності має вигляд:
![]()
де
![]()
Після логарифмування
та прирівнювання до нуля похідної від
![]() отримуємо вираз для оцінки параметра
отримуємо вираз для оцінки параметра
![]()
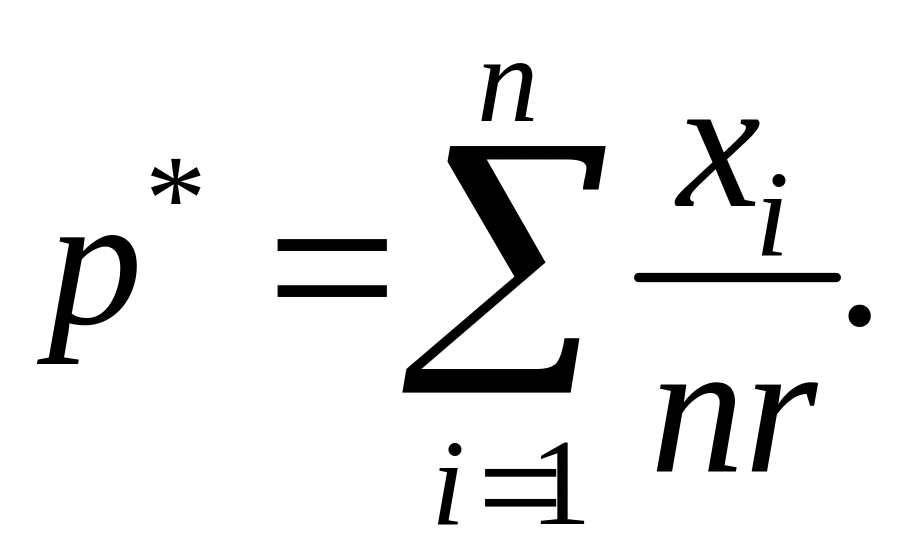
У
випадку, якщо варіанта
має
частоту
,
то оцінка параметра
![]() така:
така:
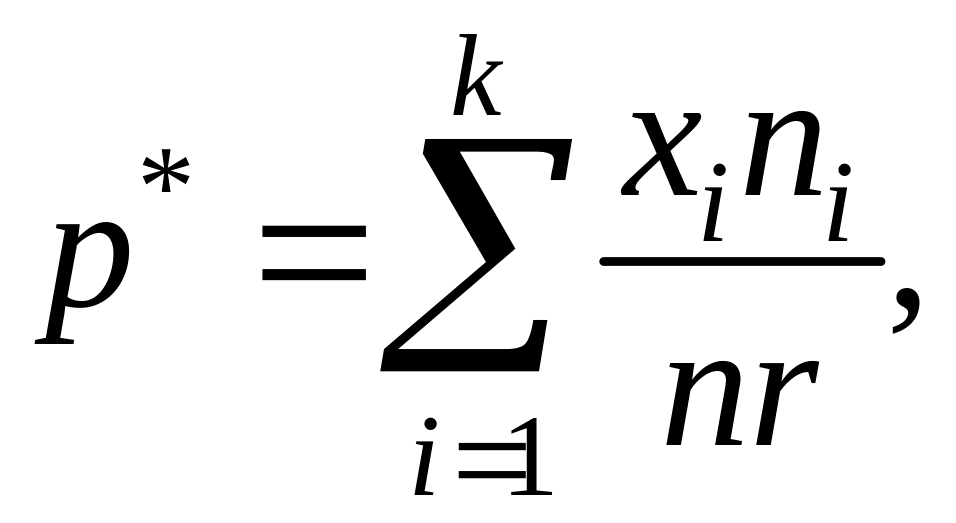
де ![]() – кількість
дослідів по
– кількість
дослідів по
![]() випробувань
у кожному.
випробувань
у кожному.
Питання для самоконтролю
1. Що називається
статистичною оцінкою
![]() невідомого параметра розподілу
випадкової величини X?
невідомого параметра розподілу
випадкової величини X?
2. Яка статистична оцінка називається незміщеною, ефективною, слушною (або змістовною, або конзистентною)?
3. Що приймають за статистичну оцінку математичного сподівання?
4. Що приймають за статистичні оцінки дисперсії, які властивості вони мають?
5. Що називається
виправленою дисперсією
![]()
6. Які існують методи статистичного оцінювання параметрів розподілу, у чому вони полягають?
Вправи
1. За результатами соціологічного опитування 1 000 осіб з питання їх середнього місячного прибутку у гривнях отримано такі результати:
|
500-750 |
750-1 000 |
1 000-1 500 |
1 500-2 000 |
2 000-2 500 |
2 500-3 000 |
|
50 |
250 |
400 |
150 |
100 |
50 |
Обчислити незміщені точкові оцінки для математичного сподівання, дисперсії та середнього квадратичного відхилення випадкової величини – середнього місячного прибутку.
2. На підприємстві виготовляється деякий вид продукції. Щомісячний обсяг випуску цієї продукції є випадковою величиною, для характеристики якої прийнято показниковий закон розподілу. Протягом шести місяців проводилось вимірювання обсягу випуску продукції. У результаті отримано такі дані:
Місяць |
1 |
2 |
3 |
4 |
5 |
6 |
Обсяг випуску |
20 |
24 |
25 |
28 |
27 |
32 |
Знайти методом
моментів оцінку параметра
![]()
3. За умови рівномірного розподілу випадкової величини отримано вибірку:
|
2 |
3 |
4 |
5 |
6 |
|
4 |
6 |
5 |
12 |
8 |
Знайти методом
моментів оцінку параметрів
та
![]()
4. Випадкова
величина
розподілена за біноміальним законом.
За наведеним статистичним розподілом
вибірки знайти точкову оцінку параметра
(![]() ):
):
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
3 |
10 |
22 |
26 |
20 |
12 |
5 |
5. Знайти методом максимальної правдоподібності оцінку параметра показникового розподілу.
6. На
основі вибірки
![]() знайти
за методом максимальної правдоподібності
точкові оцінки параметра
закону розподілу Пуассона випадкової
величини
знайти
за методом максимальної правдоподібності
точкові оцінки параметра
закону розподілу Пуассона випадкової
величини
7. Скляні однорідні вироби відправлені для реалізації у 1 000 контейнерах. Після надходження товару виявили кількість пошкоджених виробів у кожному контейнері:
|
0 |
1 |
2 |
3 |
4 |
|
785 |
163 |
32 |
16 |
4 |
Вважаючи, що кількість пошкоджених виробів описується законом Пуассона, знайти точкову оцінку параметра
