Питання для самоконтролю

1. Що називають статистичним рядом?

2. Що називається ранжуванням?

3. Що називається дискретним статистичним розподілом вибірки?

4. Що називається інтервальним статистичним розподілом вибірки?

5. Як визначається кількість інтервалів в інтервальному статистичному розподілі вибірки?

6. Чи можна інтервальний статистичний розподіл вибірки замінити дискретним?

Вправи

1. У супермаркеті проводилися спостереження за кількістю покупців, що звернулися до каси за одну годину. Спостереження проводилися протягом 30 годин, а саме: 15 діб від 10 до 11 та від 11 до 12 год. і дали такі результати: 75, 60, 100, 100, 65, 70, 60, 75, 60, 65, 75, 100, 120, 65, 60, 120, 65, 100, 75, 60, 70, 100, 60, 75, 100, 70, 65, 120, 100, 60.

Скласти дискретний статистичний розподіл частот і відносних частот випадкової величини – кількості покупців, що звернулися до каси за одну годину.

2. Для визначення терміну гарантійного обслуговування проведено дослідження величини середнього пробігу автомобілів, що знаходились в експлуатації протягом трьох років з моменту продажу автомагазином. Були отримані такі результати (тис. км): 29, 6; 4,2; 25,3; 9,9; 11,2; 16,8; 40,1; 5,4; 2,9; 9,1; 7,3; 14,4; 12,2; 26,7; 21,5; 18,3; 20,0; 29,1; 17,3; 18,0; 10,6; 12,1; 18,6; 25,0; 3,0.

Провести обробку статистичного ряду.

3. При проведенні експерименту отримали такі дані:

43, 35, 31, 48, 36, 23, 19, 43, 27, 34, 33, 25, 27, 40, 25, 21, 35, 44, 23, 35, 43, 27, 33, 32, 23, 49, 28, 22, 19, 45, 33, 35, 26, 32, 49, 36, 31, 42, 32, 37, 30, 17, 31, 30, 40, 28, 44, 16, 26, 32.

Скласти інтервальний статистичний розподіл частот, а потім замінити його дискретним.

4. Штат фірми – 40 осіб. Проведено дослідження кількості робочих днів, пропущених кожним працівником протягом місяця. Результати дослідження такі: 0, 0, 13, 10, 7, 0, 3, 5, 6, 7, 7, 5, 3, 2, 0, 1, 10, 15, 9, 1, 3, 5, 10, 2, 5, 0, 5, 7, 10, 2, 5, 3, 7, 5, 3, 2, 0, 3, 1, 0. Скласти інтервальний статистичний розподіл відносних частот.

3.4. Графічне зображення статистичних розподілів

Для наочності використовують графічне зображення статистичних розподілів – полігон і гістограму.

Полігон розподілу вибірки використовується для зображення як дискретних, так й інтервальних варіаційних рядів, а гістограма – лише для інтервальних рядів.

Полігоном частот називають ламану, відрізки якої послідовно з’єднують точки координатної площини.

Полігоном відносних частот називають ламану, відрізки якої послідовно з’єднують точки координатної площини.

Схема побудови полігона частот (відносних частот):

• на осі абсцис відкладають варіанти 

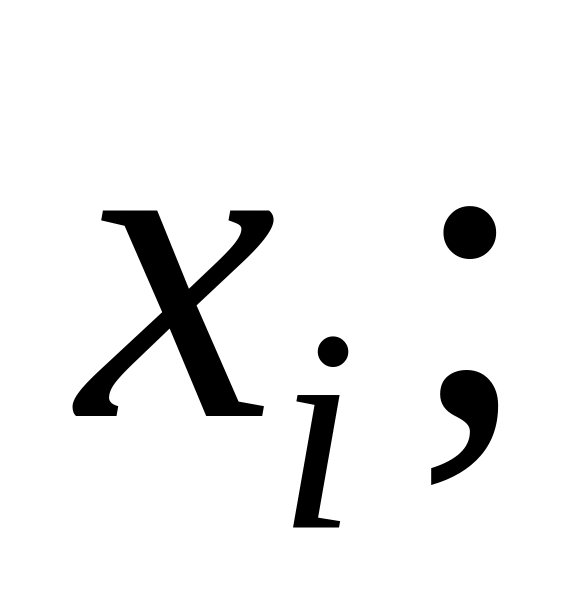
• на осі ординат – відповідні часто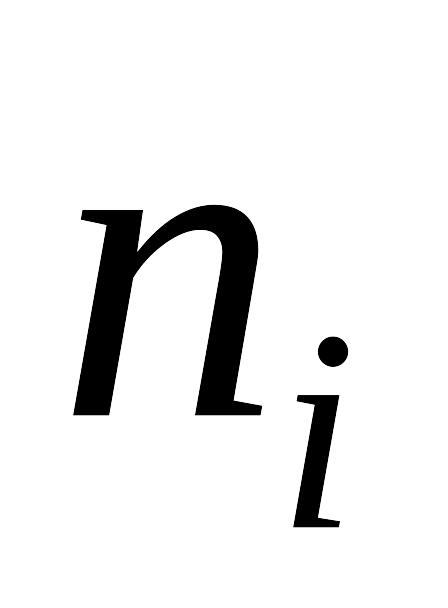ти (відносні частоти );

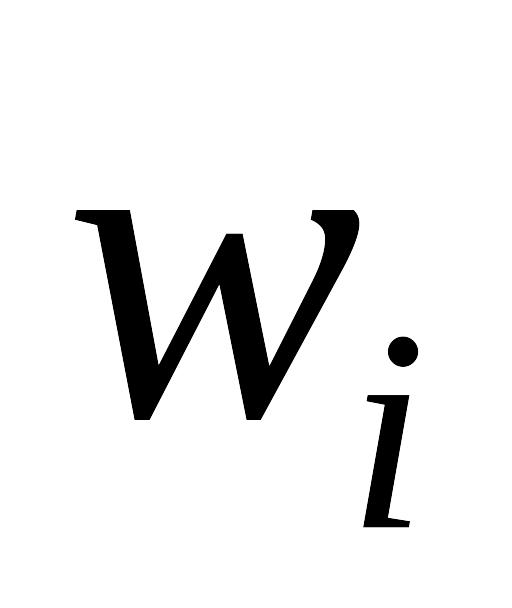• точки 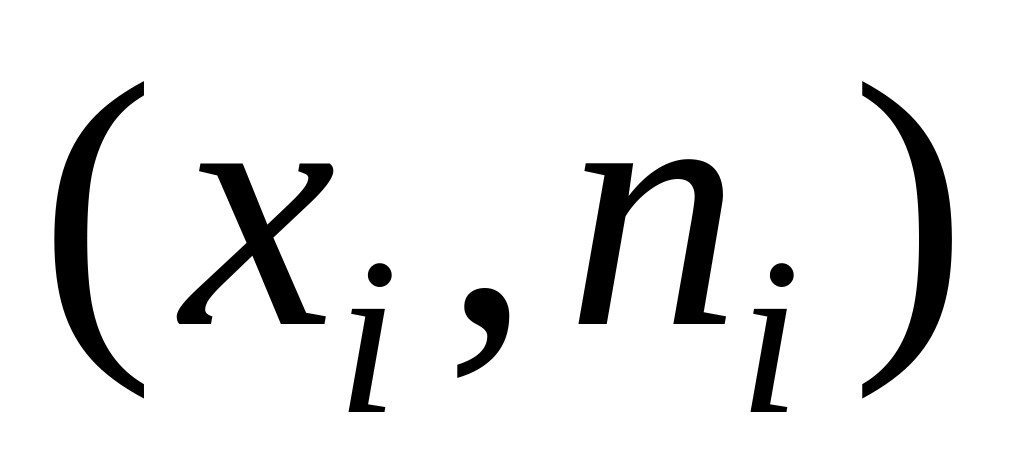( 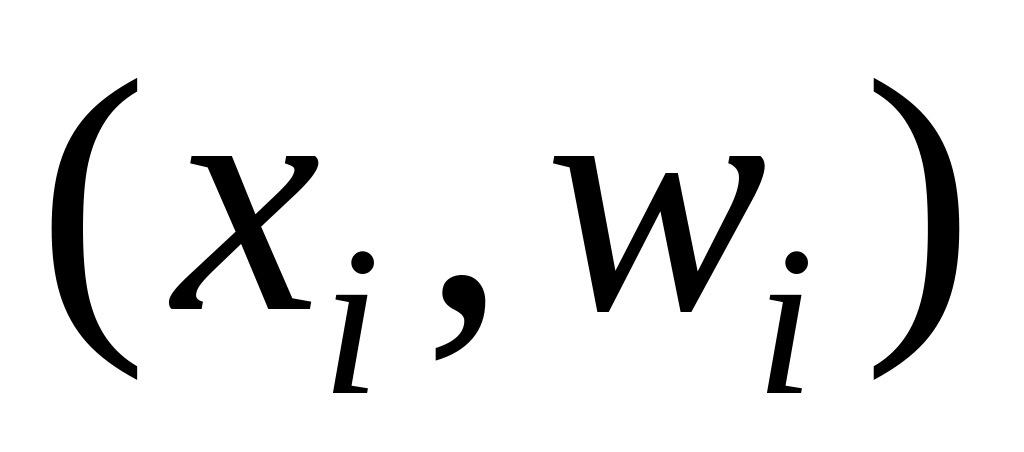) з’єднують відрізками прямих.

Гістограмою частот називається східчаста фігура, яка складена з прямокутників, основами яких є частинні інтервали а їх висоти:

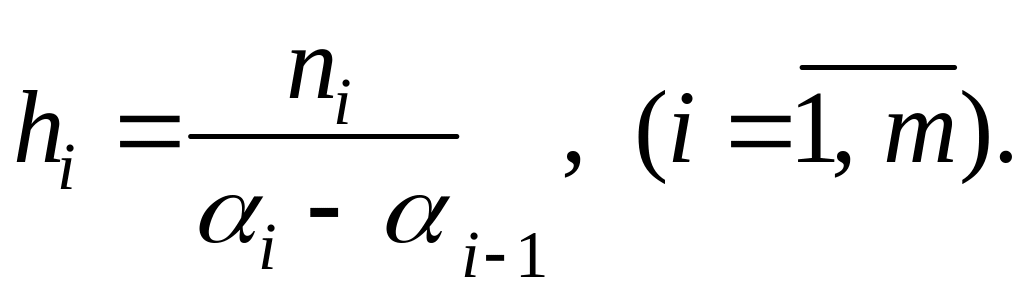(3.11)

Гістограмою відносних частот називається східчаста фігура, що складається з прямокутників, основами яких є частинні інтервали а їх висоти:

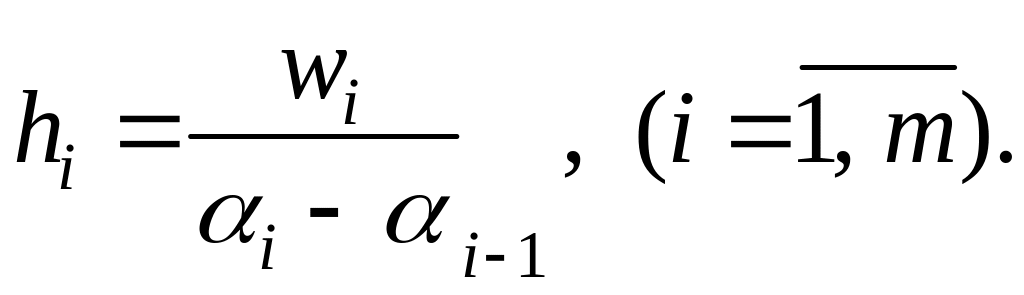(3.12)

Схема побудови гістограм частот (відносних частот):

• на осі абсцис відкладають частинні інтервали

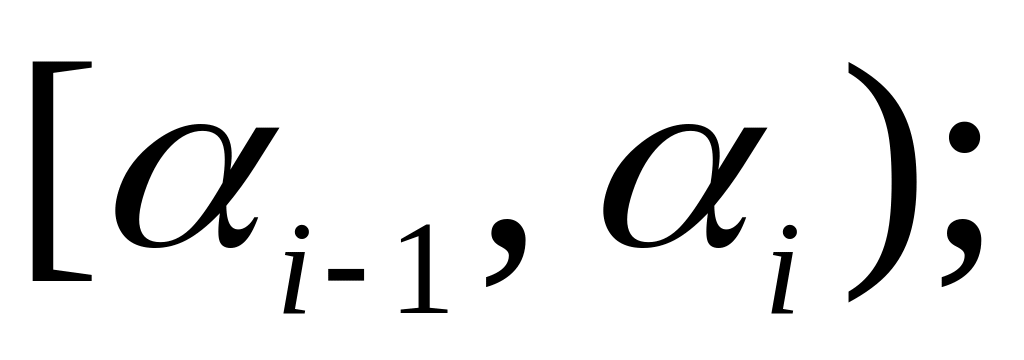
• на цих інтервалах, як на основі, будують прямокутники з висотами 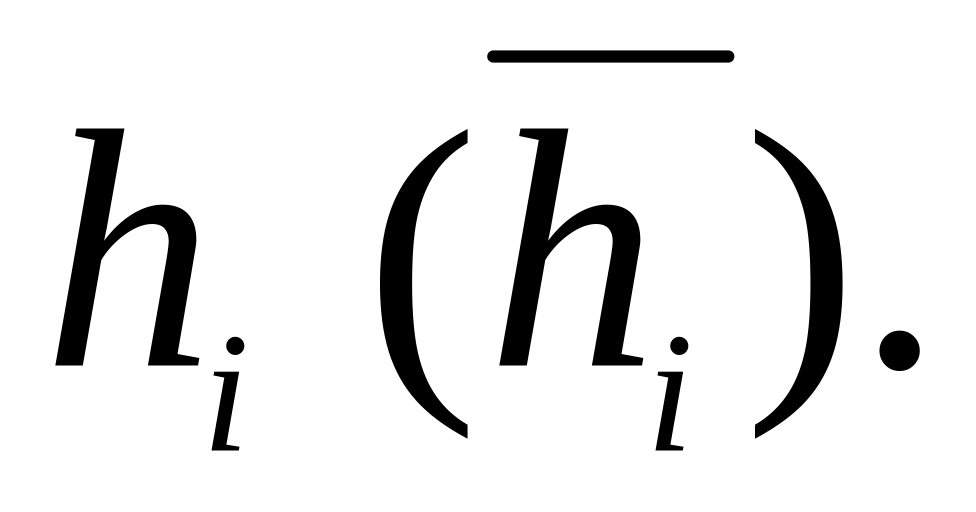Площа кожного такого прямокутника дорівнює 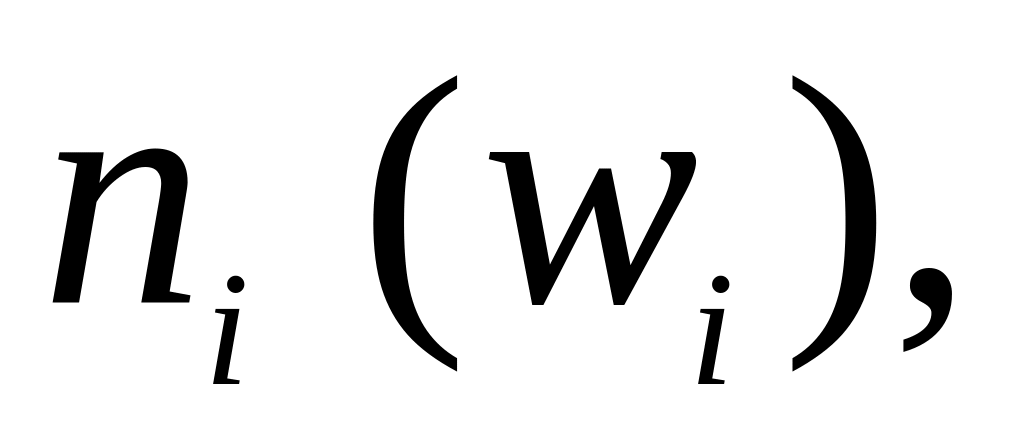а площа гістограми частот дорівнює обсягу вибірки (одиниці).

Приклад 3.2. Побудувати гістограму частот за даними прикладу 3.1, потім замінити інтервальний статистичний розподіл частот дискретним, накреслити полігон частот.

Розв’язання. Розрахуємо висоти за формулою (3.11) та даними таблиці 3.5:

Замінимо інтервальний статистичний розподіл частот дискретним. Для цього в кожному інтервалі оберемо його “представника”, тобто знайдемо середнє арифметичне , а відповідні значення частот залишимо без змін:

xi*	4,15	5,05	5,95	6,85	7,9
ni	2	4	6	5	3

Побудуємо гістограму частот:

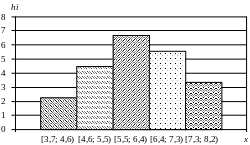
Рис. 3.1. Гістограма частот за даними прикладу 3.1

Накреслимо полігон частот:

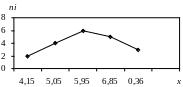
Рис. 3.2. Полігон частот за даними таблиці 3.6