Питання для самоконтролю

1. Що називається двовимірною випадковою величиною ?

2. Що називається законом розподілу ймовірностей двовимірної дискретної випадкової величини? Як знайти закони розподілу компонент?

3. Що називається функцією розподілу ймовірностей двовимірної випадкової величини?

4. Записати властивості функції розподілу двовимірної випадкової величини.

5. Записати формулу для обчислення ймовірності попадання значень неперервної випадкової величини у прямокутник .

6. Дати означення щільності розподілу ймовірностей неперервної двовимірної випадкової величини .

7. Записати властивості щільності розподілу неперервної двовимірної випадкової величини.

8. Записати формулу для обчислення попадання значень двовимірної випадкової величини у задану область через щільність її розподілу .

9. Як знайти щільності розподілу ймовірностей складових двовимірної випадкової величини.

10. Дати означення умовного розподілу складової двовимірної дискретної випадкової величини за фіксованого значення

11. Дати означення умовного розподілу складової двовимірної дискретної випадкової величини за фіксованого значення

Вправи

1. Підкидають два гральні кубики. Нехай Х – сума очок, що випадають на верхніх гранях. Написати закон розподілу випадкової величини Х.

2. Закони розподілу числа очок, які вибиває кожен із двох стрільців, такі:

а)

Х	1	2	3
p	0,1	0,3	0,6

б)

Х	1	2	3
p	0,2	0,3	0,5

Знайти закон розподілу суми очок, які вибиваються двома стрільцями.

3. Сумісний розподіл дискретних випадкових величин задано таблицею:

	–1	0	1
0	0,01	0,04	0,05
1	0,06	0,24	0,10
2	0,05	0,15	0,10
3	0,04	0,07	0,09

Знайти:

а) закони розподілу Х і Y;

б) закон розподілу Y за умови, що Х = 0;

в) ймовірність події [Х < 2, Y < 1].

Чи залежні Х і Y?

4. Сумісний розподіл дискретних випадкових величин задано таблицею:

	–1	0	1
0	0,1	0,2	0
1	0,2	0,3	0,2

Знайти:

а) закони розподілу X і Y;

б) закон розподілу X за умови, що Y = 1;

в) ймовірність події

Чи залежні Х і Y?

5. Із коробки, в якій 4 червоні, 2 сині і 3 зелені олівці, навмання взяли 3 олівці. Нехай х – число червоних, y – число синіх олівців серед відібраних. Знайти:

а) сумісний розподіл X і Y;

б) закони розподілу X і Y;

в) закон розподілу X за умови, що Y = 1;

г) ймовірність події

Чи залежні X і Y?

6. Два стрільці незалежно один від другого зробили по 2 постріли в одну і ту ж мішень. Ймовірність влучення для першого стрільця дорівнює 0,8, для другого – 0,6. Нехай X – число влучень першого стрільця, Y – другого. Знайти:

а) сумісний розподіл X і Y;

б) закони розподілу X і Y;

в) закон розподілу Y за умови, що

г) ймовірність події

Чи залежні X і Y?

7. За умовою попередньої задачі нехай: Y – загальне число влучень у мішень. Знайти:

а) сумісний розподіл X і Y;

б) закони розподілу X i Y;

в) закон розподілу Y за умови, що

г) ймовірність події .

Чи залежні X і Y?

8. По мішені робиться один постріл. Ймовірність влучення дорівнює ρ. Розглядаються 2 випадкові величини: X – число влучень, Y – число промахів. Побудувати функцію розподілу двовимірної випадкової величини .

9. Двовимірна випадкова величина має щільність ймовірності:

Знайти:

а) величину А;

б) функцію розподілу ;

в) ймовірність попадання випадкової точки (x, y) у квадрат, обмежений лініями

10. Задана функція розподілу двовимірної випадкової величини:

Знайти щільність розподілу

11. Система має щільність ймовірності:

Знайти:

а) С;

б) функцію розподілу F(x, y).

12. Система випадкових величин задана щільністю ймовірності:

Знайти:

а) функцію розподілу F(x, y);

б) ймовірність попадання випадкової точки в прямокутник, обмежений лініями:

13. Задана функція розподілу системи

Знайти:

а) ймовірність попадання випадкової точки у квадрат

б) щільність ймовірності системи

14. Двовимірна випадкова величина задана щільністю розподілу: в області D і – поза цією областю. Область D – трикутник, обмежений прямими

Знайти:

а) величину А;

б) щільності розподілу складових.

15. Дана щільність розподілу системи

у квадраті – поза цим квадратом. Знайти функцію розподілу F(x, y).

16. Система має щільність ймовірності

Знайти:

17. Щільність сумісного розподілу неперервної системи величин у квадраті , , поза квадратом – Довести, що складові і незалежні.

Вказівка. Впевнитись, що безумовні щільності розподілу складових дорівнюють відповідним умовним щільностям.

18. Дана функція розподілу двовимірної випадкової величини

Знайти функції розподілів компонент. Перевірити незалежність випадкових величин.

19. Неперервна двовимірна випадкова величина рівномірно розподілена всередині прямокутного трикутника з вершинами О(0; 0), А(0; –8), В(8; 0). Знайти щільність двовимірної випадкової величини щільність компонент. Перевірити, чи залежні Х і Y.

20. Система рівномірно розподілена в трикутнику, обмеженому прямими Знайти: Перевірити, чи залежні Х і Y.

21. Задані щільності розподілу незалежних складових неперервної двовимірної випадкової величини

Знайти:

а)

б)

22. Двовимірну випадкову величину . Задано щільністю розподілу ймовірностей:

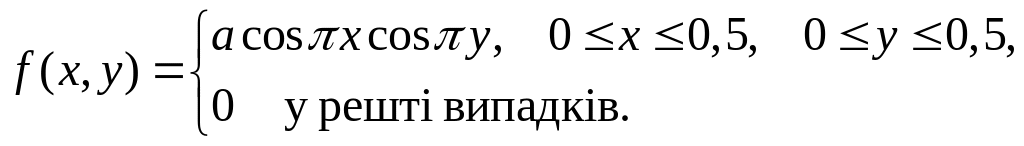
Знайти:

а) сталу а;

б) умовні щільності розподілів складових.

23. Незалежні випадкові величини Х і Y. Задані щільностями ймовірностей

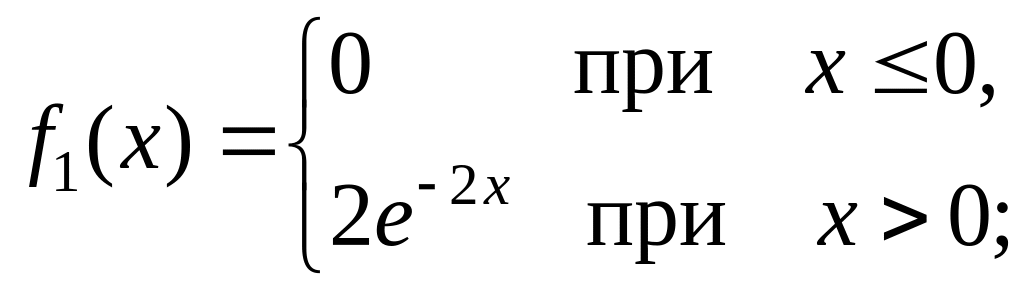
Знайти:

а)

б)