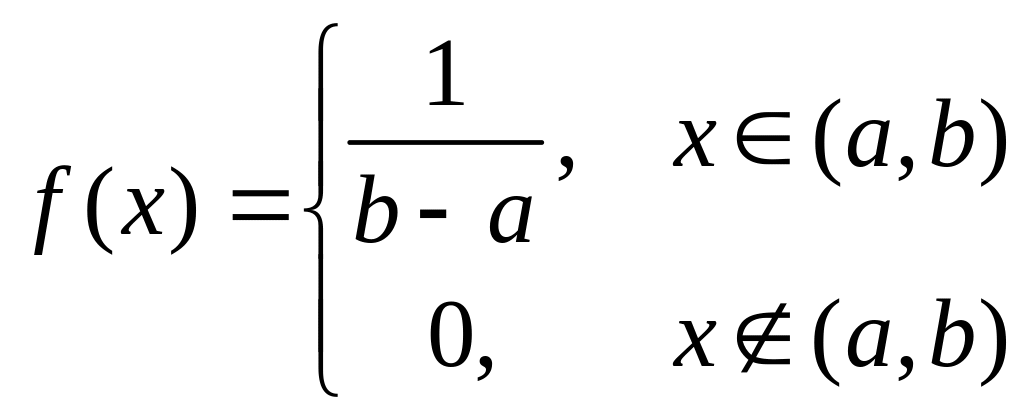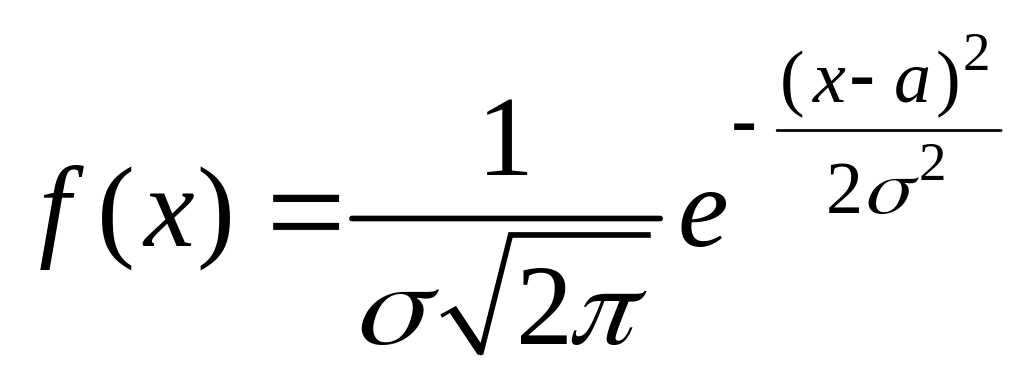- •Т.І. Малютіна, к.А. Дахер вища математика для економістів
- •Теорія ймовірностей і математична статистика
- •Розділ і випадкові події
- •1.1. Простір елементарних подій. Випадкові події та операції над ними. Комбінаторика
- •1.1.1. Основні поняття теорії ймовірностей. Операції над подіями
- •Питання для самоконтролю
- •1.1.2. Елементи комбінаторики
- •Розв’язування комбінаторних задач
- •Питання для самоконтролю
- •1.2. Ймовірність випадкової події. Способи обчислення ймовірностей випадкових подій
- •1. Класичне означення ймовірності
- •2. Статистична ймовірність
- •3. Геометрична ймовірність
- •Питання для самоконтролю
- •1.3. Теореми додавання і множення ймовірностей. Умовна ймовірність
- •Питання для самоконтролю
- •1.4. Формула повної ймовірності. Формула Байєса
- •Питання для самоконтролю
- •1.5. Послідовні незалежні випробування
- •1.5.1. Формула Бернуллі
- •1.5.2. Формула Пуассона
- •1.5.3. Локальна теорема Муавра-Лапласа
- •1.5.4. Інтегральна теорема Муавра-Лапласа
- •Питання для самоконтролю
- •Розділ іі випадкові величини
- •2.1. Одновимірні випадкові величини. Способи задання
- •2.1.1. Дискретні випадкові величини. Функція розподілу. Основні закони розподілу
- •2.1.2. Неперервні випадкові величини. Щільність розподілу. Основні закони розподілу
- •Питання для самоконтролю
- •2.2. Числові характеристики випадкових величин
- •1. Математичне сподівання
- •2. Дисперсія та середнє квадратичне відхилення
- •3. Початкові та центральні моменти
- •4. Мода і медіана
- •Числові характеристики деяких розподілів
- •Питання для самоконтролю
- •2.3. Рівномірний, показниковий, нормальний розподіли
- •Питання для самоконтролю
- •2.4. Граничні теореми теорії ймовірностей. Закон великих чисел і центральна гранична теорема. Нерівність ЧебишОва
- •2.4.1. Лема Чебишова
- •2.4.2. Теорема Чебишова
- •2.4.3. Теорема Бернуллі
- •Питання для самоконтролю
- •2.5. Двовимірна випадкова величина
- •2.5.1. Закон розподілу ймовірностей. Закони розподілу компонент
- •2.5.2. Функція розподілу двовимірної випадкової величини та її властивості
- •2.5.3. Щільність сумісного розподілу ймовірностей неперервної двовимірної випадкової величини, основні властивості. Ймовірність попадання випадкової точки в задану область
- •2.5.4. Умовні закони розподілу складових системи дискретних і неперервних випадкових величин. Залежні та незалежні випадкові величини
- •1. Випадок дискретної величини
- •2. Випадок неперервної величини
- •Питання для самоконтролю
- •2.5.5. Числові характеристики двовимірної випадкової величини. Кореляційний момент і коефіцієнт кореляції
- •Числові характеристики двовимірної випадкової величини
- •Питання для самоконтролю
- •2.5.6. Умовні числові характеристики двовимірної випадкової величини. Регресія
- •1. Випадок дискретної випадкової величини
- •2. Випадок неперервної випадкової величини
- •Питання для самоконтролю
- •Розділ III елементи математичної статистики
- •3.1. Предмет та основні завдання математичної статистики
- •3.2. Генеральна та вибіркова сукупності. Вибірка. Способи відбору
- •Питання для самоконтролю
- •3.3. Статистичний розподіл вибірки
- •Питання для самоконтролю
- •3.4. Графічне зображення статистичних розподілів
- •3.5. Емпірична функція розподілу. Кумулята
- •Питання для самоконтролю
- •3.6. Числові характеристики статистичного розподілу вибірки
- •Питання для самоконтролю
- •3.7. Статистичні оцінки параметрів генеральної сукупності
- •3.7.1. Статистичні оцінки невідомих параметрів розподілу та їх властивості
- •3.7.2. Статистична оцінка математичного сподівання
- •3.7.3. Статистична оцінка дисперсії. Виправлена дисперсія
- •3.7.4. Метод моментів статистичного оцінювання параметрів розподілу
- •3.7.5. Метод максимуму правдоподібності статистичного оцінювання параметрів розподілу
- •Питання для самоконтролю
- •3.8. Інтервальні оцінки параметрів розподілу
- •3.8.1. Надійність. Інтервал довіри
- •3.8.2. Розподіл – “хі-квадрат”
- •3.8.3. Розподіл Стьюдента
- •3.8.4. Розподіл Фішера-Снедекора
- •3.8.5. Інтервальні оцінки для математичного сподівання
- •3.8.6. Оцінка істинного значення вимірюваної величини
- •3.8.7. Інтервали довіри для середнього квадратичного відхилення нормально розподіленої випадкової величини
- •3.8.8. Оцінка точності вимірювань
- •Питання для самоконтролю
- •3.9. Елементи теорії кореляції
- •3.9.1. Функціональна, статистична й кореляційна залежності
- •3.9.2. Вибірковий коефіцієнт кореляції. Коефіцієнт детермінації
- •Питання для самоконтролю
- •3.9.3. Основні поняття і методи регресійного аналізу
- •3.9.4. Метод найменших квадратів
- •Питання для самоконтролю
- •3.10. Статистична перевірка статистичних гіпотез
- •3.10.1. Статистичні гіпотези. Помилки першого та другого роду
- •3.10.2. Статистичний критерій перевірки нульової гіпотези
- •Питання для самоконтролю
- •3.10.3. Перевірка гіпотези про закон розподілу. Критерій згоди Пірсона
- •3.10.4. Перевірка гіпотези про порівняння середнього значення ознаки генеральної сукупності зі стандартом
- •3.10.5. Перевірка гіпотези про рівність дисперсій двох незалежних випадкових величин
- •3.10.6. Перевірка гіпотези про значущість коефіцієнта кореляції
- •Питання для самоконтролю
- •Список використаної та рекомендованої літератури
- •Додаток а
- •Додаток б
- •Додаток в
- •Додаток г
- •Додаток д Критичні точки розподілу f Фішера-Снедекора
- •Додаток е
- •Додаток ж Значення
- •Вища математика для економістів
- •40030, М. Суми, вул. Петропавлівська, 57
Числові характеристики деяких розподілів
Біномний розподіл |
Х |
0 |
1 |
… |
п |
|
|
Р |
|
|
… |
|
|||
Розподіл Пуассона |
Х |
0 |
1 |
2 |
… |
п |
|
Р |
|
|
|
… |
|
||
Рівномірний розподіл |
|
|
|||||
Показниковий розподіл |
|
|
|||||
Нормальний розподіл |
|
|
|||||
Питання для самоконтролю
1. Що називається математичним сподіванням дискретної випадкової величини Х? Дисперсією? Середнім квадратичним відхиленням? Навести їх властивості.
2. Як обчислюються математичне сподівання і дисперсія неперервної випадкової величини?
3. Дати означення початкового моменту випадкової величини.
4. Дати означення центрального моменту випадкової величини.
5. Який зв’язок між центральними і початковими моментами випадкової величини?
6. Дати означення моди і медіани випадкової величини.
Вправи
1. Математичне сподівання і дисперсія випадкової величини Х відповідно дорівнюють 2 і 10. Знайти М(2Х + 5) і D(2Х + 5).
2. Випадкова
величина Х
набуває трьох значень
![]()
![]()
![]() Відомо, що
Відомо, що
![]() .
Знайти закон розподілу Х.
.
Знайти закон розподілу Х.
3. Визначити математичне сподівання (середнє число), дисперсію та середнє квадратичне відхилення випадкової величини X, розподіл ймовірностей якої задано таблицею:
а)
xi |
10 |
20 |
30 |
40 |
50 |
pi |
0,18 |
0,26 |
0,32 |
0,20 |
0,04 |
б)
xi |
9 |
10 |
20 |
40 |
50 |
pi |
0,1 |
0,15 |
0,15 |
0,4 |
0,2 |
в)
xi |
–1 |
0 |
2 |
3 |
5 |
pi |
0,15 |
0,3 |
0,15 |
0,2 |
0,2 |
г)
xi |
0 |
1 |
2 |
3 |
4 |
pi |
0,2 |
0,4 |
0,3 |
0,08 |
0,02 |
4. Випадкова величина
X набуває двох можливих значень
![]() та
та
![]() з ймовірностями відповідно
з ймовірностями відповідно
![]() та
та
![]() Знайти х1 та х2 і
записати її закон розподілу, якщо:
Знайти х1 та х2 і
записати її закон розподілу, якщо:
а) ![]()
б) ![]()
в) ![]()
г) ![]()
5. Заданий закон розподілу дискретної випадкової величини X:
X = хi |
–3 |
–2 |
1 |
3 |
5 |
7 |
Р(Х = хi) = pi |
a |
1,5 a |
0,5 a |
3,5 a |
2,5 a |
a |
Знайти:
а) параметр а;
б) ![]()
в) функцію розподілу ймовірностей та побудувати її графік;
г) М(Х), D(X), AS, ES.
6. Випадкові
величини Х
і У
незалежні. Відомо, що
![]()
![]() Знайти
Знайти
![]() ,
якщо:
,
якщо:
1) ![]()
2) ![]()
3) ![]()
7. Партія, що нараховує 10 виробів, містить 3 браковані. Зі всієї партії довільно вибирають 3 вироби з метою перевірки їх якості. Знайти математичне сподівання та дисперсію кількості бракованих виробів, що містяться в такій довільній вибірці.
8. Імовірність виготовлення стандартної деталі дорівнює 0,96. Для перевірки навмання взято 300 деталей. Скільки в середньому виявиться бракованих деталей серед перевірених? Яким є середнє квадратичне відхилення кількості бракованих деталей?
9. Середнє число викликів, що находять на АТС за хвилину, дорівнює 120. Знайти ймовірності таких подій:
А = {за дві секунди надійде менше двох викликів};
В = {за 1 секунду на АТС надійде хоч би один виклик};
С = {за 3 секунди надійде не менше шести викликів}.
10. Два стрільці
незалежно один від одного зробили по п
пострілів у мішень. Ймовірність влучення
при кожному пострілі для першого стрільця
дорівнює
![]() для другого –
для другого –
![]() Позначимо через
Позначимо через
![]() і
і
![]() число влучень у мішень першого і другого
стрільців відповідно. Знайти:
число влучень у мішень першого і другого
стрільців відповідно. Знайти:
а) ![]()
б) ![]()
в) ![]()
г) ![]()
11. Обчислити D(X), (X), якщо закон розподілу ймовірностей дискретної випадкової величини X задано функцією розподілу
![]()
12. Випадкова величина Х має щільність ймовірності
![]()
Знайти
![]() і
і
![]()
13. У задачах дано
![]() – функцію розподілу випадкової величини
Х. Потрібно:
– функцію розподілу випадкової величини
Х. Потрібно:
1) знайти функцію щільності ймовірностей
2) обчислити М(Х) і D(X);
3) побудувати
графіки функцій
і
![]()
а)![]()
б)![]()
в)![]()
14. У задачах дано
![]() – функцію щільності ймовірностей.
Знайти функцію розподілу, обчислити
M(X )
і D(X ):
– функцію щільності ймовірностей.
Знайти функцію розподілу, обчислити
M(X )
і D(X ):

15. Дано закон розподілу випадкової величини Х:
x |
2 |
4 |
6 |
8 |
Р |
0,4 |
0,3 |
0,2 |
0,1 |
x |
2 |
3 |
5 |
Р |
0,1 |
0,4 |
0,5 |
Знайти:
а) початкові і центральні моменти перших чотирьох порядків;
б) асиметрію та ексцес цієї випадкової величини.
16. Дана щільність ймовірності випадкової величини Х
![]()
Знайти:
а) початкові та центральні моменти перших чотирьох порядків;
б) асиметрію та ексцес цієї випадкової величини.
17. Знайти
моду медіану випадкової величини Х,
заданої функцією розподілу
![]()
18. Випадкова
величина Х
в інтервалі (–1; 1) задана щільністю
розподілу
![]() поза цим інтервалом
поза цим інтервалом
![]()
Знайти:
а) моду;
б) медіану Х.