15.Динамічне програмування: мат. Моде-ль та її види.

На практиці існують випадки, коли об’єкт постійно змінюється за часом або у просторі, для таких задач треба знайти оптимальну траєкторію поведінки об’єкта. Тобто, для роз-в’язання таких задач необхідно розглядати об’єкт у динаміці, здійснюючі контроль за йо-го поведінкою. Для розв’язання таких задач використовують 2 підходи:1)За допомогою стат. методів. Розвязки цими методами мають значні обсяги обчислювань.2)Розглядати за-дачу поетапно використовуючи однотипні формули для поведінки об’єкта, для цих мето-дів розглядають стани об’єкта поступово, наб-лижуючись до ext точок. Такий підхід об’єдну-ється в процедуру динамічного програмував-ня. Щоб розв’язати задачу цим методом необ-хідно виконувати наступні умови: 1) Задача повинна мати багатокрокову структуру. 2) Цільова функція повинна бути адитивною

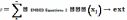може бути

мультиплікативною ∑=П. 3)Подальша поведінка об’єкта не залежить від того, як він вів себе на попередніх кроках, а залежить від стану об’єкта на поточному кроці.(принцип Беллмана).4)обчислена процедура не залежи-ть від кількості оптимальності та обсягів ресу-рсів.(принцип вкладеності). Тобто, якщо розв’язується задача великої розмірності, то усі задачі меншої розмірності входять до розв’язку більшої розмірності.

14.Метод потенціалів в тз.

Цей метод використовує теорію двоїстої пари задач.За допомогою неї знаходяться фактичні оціночні коефіцієнти C^/_ij, які порівнюються з відповідними оцінками C_ij. Алгоритм пошуку: 1) Для всіх базисних змінних складається рівняння потенціалів:

Х_ij ≠0 ; U_i +V_j= C_ij. U_i та V_j –змінні двоїстої пари задач; Ui- відповідає та характеризує поведінку і-го постачальника; Vj- відповідає та характеризує поведінку j-го споживача.2)Складена система рівнянь поте-нціалів розв’язується відносно U_i V_j. Одержана система розв’язується тільки тоді, коли різниця між кількістю змінних та кількістю рівнянь =1. У цьому випадку одна із змінних прирівнюється до 0. Потім, система розв’язує-ться відомими методами. Найбільш простим є метод: проводиться аналіз кожного рівнян-ня і знаходяться інші змінні системи. Якщо різниця між кількостями змінних >1, то у та-кому вигляді система не розв’язується і назв. виродженою.Щоб розв’язати вироджену сис-тему, необхідно привести її до нормального вигляду. Для цього, одна з нульових змінних, умовно вважається фіктивною базисною змі-нною і рівняння цієї фіктивної змінної допи-сується до системи рівнянь U_i V_j; 3) Знаход-ження фактичних оціночних коефіцієнтів C^/_ij для усіх нульових змінних: X_ij = 0 ;U_i + V_{j =}C^/_ij. 4) Аналіз на оптимальність: C_ij=C^/_ij. 5) Якщо одержаний план не оптимальний, то необхі-дно побудувати наступний варіант розподілу. Для цього будується цикл перерозподілу ресу-рсів. Початком цього циклу є нульова змінна, яка більш всього порушує умови оптимальн.

max|C^/_ij -C_ij|.Інші вершини циклу знаходяться в базисних змінних. Практично такі цикли будуються в центральній частині таблиці потужності. Геометрична інтерпретація така: 6)Знаходження величини корегування змін-ної, для цього складається послідовність змін-ної циклу, а потім ведеться розмітка цих змін-них знаків «+»,«-».Величина корегування = мінімал. значенню змінної зі знаком «-». ∆=min{ X_ij ^«-»}.Усі змінні, які ввійшли до циклу корегуються на величину ∆ з урахуванням знаків розмітки. X_ij= X_ij ± ∆. Змінні, які не ввій-шли до циклу не корегуються. Одержаний новий план розподілу необхідно проаналізу-вати на оптимальність, починаючи з пункту 1,2 і тд. Примітка: існують випадки, коли не-можливо побудувати цикл розподілу за правилами, щоб побудувати цикл необхідно одну із нульових змінних вважати фіктивною базисною і побудувати використовуючи цю змінну в нормальний цикл. Фіктивна змінна обов’язково в наступній розмітці зі знаком «+». Цей цикл- вироджений.