11.Тз: види виродженої задачі.

Загальна кількість рівнянь математичної мо-делі транспортної за­дачі дорівнює m+n , але одне з цих рівнянь є наслідком решти, оскільки . Тому в закритій транспортній задачі система рівнянь має m+n-1 незалежних рівнянь, тобто ранг мат-риці системи обмежень дорівнює m+n-1. Це означає, що кількість змінних x_ij≠0 дорівнює m+n-1.Проте на практиці зустрічаються ви-падки, коли кількість базисних змінних мен-ша від m+n-1. У цьому разі розв'язок Назива-ють вирод­женим; його дістають тоді, коли множина змінних x_ij знайденого пла­ну розпадається на непов'язані підмножини. Ступінь виродження плану залежить від різ-ниці між m+n-1 та кількістю базисних змін-них. При застосуванні, методів розв'язання транспортної задачі необхідно виключити випадок виродження, оскільки розв'язування такої задачі зацик­люватиметься, тобто повер-татиметься до раніше знайденого плану. Для цього використовують таку рекомендацію: у знайдений план розподілу ресурсів уводять кількість умовно базисних змінних з нульови-ми значеннями, потрібну до числа m+n-1. Ці змінні(фіктивні0 вибирають так,щоб вони бу-ли на перетині рядка та колонки таблиці роз-поділу,в яких є хоча б одна баз.змінна x_ij≠0. Після цього задача стає штучно не вироджен.

14.Метод потенціалів в тз

Цей метод використовує теорію двоїстої пари задач. За допомогою неї знаходяться факти-чні оціночні коефіцієнти C^/_ij, які порівнюються з відповідними оцінками C_ij. Алгоритм пошу-ку: 1) Для всіх базисних змінних складається рівняння потенціалів: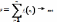

Х_ij ≠0 ; U_i +V_j= C_ij. U_i та V_j –змінні двоїстої пари задач; Ui- відповідає та характеризує поведінку і-го постачальника; Vj- відповідає та характеризує поведінку j-го споживача. 2) Складена система рівнянь потенціалів розв’я-зується відносно U_i V_j. Одержана система розв’язується тільки тоді, коли різниця між кількістю змінних та кількістю рівнянь =1. У цьому випадку одна із змінних прирівнюється до 0. Потім, система розв’язується відомими методами. Найбільш простим є метод: прово-диться аналіз кожного рівняння і знаходяться інші змінні системи. Якщо різниця між кіль-костями змінних >1, то у такому вигляді система не розв’язується і називається вирод-женою. Щоб розв’язати вироджену систему, необхідно привести її до нормального вигля-ду.Для цього,одна з нульових змінних, умовно вважається фіктивною базисною змінною і рівняння цієї фіктивної змінної дописується до системи рівнянь U_i V_j; 3) Знаходження фактичних оціночних коефіцієнтів C^/_ij для усіх нульових змінних: X_ij = 0 ;U_i + V_{j =}C^/_ij. 4) Аналіз на оптимальність: C_ij=C^/_ij. 5) Якщо одержаний план не оптимальний, то необхід-но побудувати наступний варіант розподілу. Для цього будується цикл перерозподілу ресу-рсів. Початком цього циклу є нульова змінна, яка більш всього порушує умови оптимально-сті. max |C^/_ij -C_ij|. Інші вершини циклу знахо-дяться в базисних змінних. Практично такі цикли будуються в центральній частині таблиці потужності.  Геометрична  інтерпрет-ація така:6)Знаходження величини корегува-ння змінної, для цього складається послідов-ність змінної циклу, а потім ведеться розмітка цих змінних знаків «+»,«-».Величина корегу-вання = мінімальному значенню змінної зі знаком «-».∆= min{ X_ij ^«-« }.Усі змінні, які ввій-шли до циклу корегуються на величину ∆ з урахуванням знаків розмітки. X_ij= X_ij ± ∆. Змінні, які не ввійшли до циклу не корегують-ся.Одержаний новий план розподілу необхі-дно проаналізувати на оптимальність, почи-наючи з пункту 1,2 і тд. Примітка : існують випадки, коли неможливо побудувати цикл розподілу за правилами, щоб побудувати цикл необхідно одну із нульових змінних вважати фіктивною базисною і побудувати використовуючи цю змінну в нормальний цикл.Фіктивна змінна обов’язково в наступній розмітці зі знаком «+». Цей цикл- вироджен.