- •1.Загальна задача лінійного програмування.
- •2.Графічний метод розв’язування злп.
- •3.Симплексний метод: ідея, вимогита умови оптимальності.
- •9.Транспортна задача: особливості, типи, математична модель.
- •6.Двоїста пара задач: типи та алгоритм перетворення.
- •7.Теореми двоїстості.
- •8.Розв’язування двоїстої задачі.
- •10.Умови оптимальності в тз, її обґрунтування.
- •11.Тз: види виродженої задачі.
- •14.Метод потенціалів в тз
- •45.Узагальнений метод найменших квадратів (метод Ейткена).
- •12.Методи будування базисних планів при розв’язуванні тз.
- •15.Динамічне програмування: мат. Моде-ль та її види.
- •14.Метод потенціалів в тз.
- •47. Метод визначення гетеро- за тестом Гольфельда-Квандта.
- •16.Метод динамічного програмування: властивості, переваги, недоліки.
- •13.Альтернативний оптимум в тз
- •19.Розв’язування задач методом динамічного програмування.
- •20.Задача про призначення: її модель та алгоритм.
- •21.Задача про кільцевий маршрут: модуль та розв’язування.
- •22.Угорський метод.
- •24.Задача про максимальний потік: модель та алгоритм.
- •25.Задача про найкоротшу відстань: модель та алгоритм.
- •26.Загальна економетрична модель та її постановка.
- •27.Вимоги та етапи будування економетричної моделі.
- •28.Специфікація економетричної моделі.
- •46.Метод визначення гетероскедастичності за μ-критерієм.
- •30.Метод найменших квадратів.
- •31.Передумови застосування мнк.
- •33.Оцінка тісноти зв’язку між змінними рівнянь регресії.
- •34.Стандартні похибки при оцінці параметрів моделі.
- •35.Оцінка значущості зв’язку між змінними моделі.
- •37.Стат. Критерії перевірки значущості зв’язку між змінними моделі.
- •38.Поняття мультиколінеарності, її негативність, наслідки та ознаки
- •40.Визначення мультиколінеарності за допомогою критерія Пірсона.
- •41.Визначення мультиколінеарності за допомогою критерія Стьюдента.
- •42.Визначення мультиколінеарності за допомогою критерія Фішера.
- •39.Напрямки усунення мульт-.
- •43.Алгоритм Феррара-Глобера для виявлення мульт- (загальна частина).
- •44.Гетероскедастичність та її вплив на оцінки параметрів моделі.
- •48.Визначення гетероскедастичності за тестом Спірмана.
- •50.Автокореляція: зміст, причини виникнення та її наслідки.
- •51.Методи визначення автокореляції.
- •Графічний метод розв’язування злп.
9.Транспортна задача: особливості, типи, математична модель.
Змістова постановка ТЗ наступна:
Необхідно знайти оптимальний план переве-зення вантажу від m (i=1,m) постачальників до n (j=1,n) споживачів з мінім. трансп. витра-тами.Витрати по перевезенню одиниці ванта-жу від і-того постачальника до j-го споживача задано коефіцієнтами Сіj. Кожен і-тий поста-чальник х-ся можливостями аі, а кожен j-тий споживач - попитом bj.
Позначио через Хіj обсяги перевезень вантажу від і-тої точки до j-тої точки. Тоді мат. модель має наступний вигляд:
1.
2. -
по постачальникам
-
по постачальникам
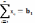 -
обмеження по споживачам.
-
обмеження по споживачам.
3.Обсяги
перевезень повинні бути невід’ємними
 Для
практичного використання існує матрична
форма: аі=а1,
а2...аm
bj=b1,b2...bn
Для
практичного використання існує матрична
форма: аі=а1,
а2...аm
bj=b1,b2...bn
Методи розв`язування трансп. задачі існують тільки для збалансованого типу, тобто, коли:
аі=bi(сума
доставки=сумі споживання).Якщо задача
незбалансована, то її приводять до
збалансов. типу за допомогою ввода
фіктив-ної точки:або споживача, або
постачальника. Потужність фіктивної
точки=величині розбалансу. Для фіктивної
точки всі оціночні коефіцієнти Сіj=0.
Якщо вводиться фіктив-ний постачальник,
то матриця С доповнюєть-ся нульовим
рядком, якщо вводиться фіктив. споживач
- нульовим стовпцем. Кожний оде-ржаний
план розв`язку х-ся фактич. Оцінок-ними
коефіцієнтами Cij. План вважається
оп-тимальним, якщо всі фактичні
коефіцієнти не перевищують відповідних
планових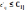 .
.
6.Двоїста пара задач: типи та алгоритм перетворення.
Для
кожної задачі оптимізації існує обернена
задача, яка називається двоїстою. За
допомо-гою такої двоїстої пари, можливо
проводити аналіз одержаного оптимального
варіанту на такі показники: рентабельність
виробництва готової продукції,
дефіцитність вихідних ресурсів, питання
розширення асортименту готової
продукції, питання зміни обсягів
вихідних ресурсів на величину цільової
ф-ії та ін. Якщо відома математична
модель прямої задачі(ПЗ), математична
модель двоїстої задачі(ДЗ) знаходиться
за наступним алгори-тмом: 1.Кількість
змінних ДЗ  дорівнює кіль-кості обмежень ПЗ, а
кількість обмежень ДЗ дорівнює кількості
змінних ПЗ
дорівнює кіль-кості обмежень ПЗ, а
кількість обмежень ДЗ дорівнює кількості
змінних ПЗ 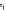 .
2.Щоб побудувати математичну модель ДЗ
необхід-но структуру моделі ПЗ привести
до наступ-ного вигляду: Якщо цільова
функція ПЗ пря-мує до мінімуму,то усі
обмеження повинні бути
.
2.Щоб побудувати математичну модель ДЗ
необхід-но структуру моделі ПЗ привести
до наступ-ного вигляду: Якщо цільова
функція ПЗ пря-мує до мінімуму,то усі
обмеження повинні бути

3.Оціночні
коефіцієнти в цільовій функції ПЗ  становляться правими частинами
відповід-них обмежень ДЗ. А праві частини
обмежень ПЗ становляться оціночними
коефіцієнтами цільової функції ДЗ.
4.Нормативні коефіцієн-ти затрат вихідних
ресурсів
становляться правими частинами
відповід-них обмежень ДЗ. А праві частини
обмежень ПЗ становляться оціночними
коефіцієнтами цільової функції ДЗ.
4.Нормативні коефіцієн-ти затрат вихідних
ресурсів  представляють-ся у вигляді матриці
представляють-ся у вигляді матриці
 ,
потім вона транс-понується і одерж.
коефіцієнти запис. Обме-ження ДЗ при
відповідних змінних. Для задач оптимізації
використання вихідних ресурсів мат.
моделі двоїстої пари задач мають вигляд:
,
потім вона транс-понується і одерж.
коефіцієнти запис. Обме-ження ДЗ при
відповідних змінних. Для задач оптимізації
використання вихідних ресурсів мат.
моделі двоїстої пари задач мають вигляд:
1.Пряма задача:
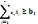 ;
;

2.Двоїста задача:

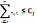 ;
;
 ;
;
Дана двоїста пара задач відноситься до симе-тричної пари, типічним представником такої пари є задача оптимального використання ресурсів. Якщо в ПЗ є обмеження у вигляді строгих рівнянь, то така задача відноситься до несиметричної пари, де знак обмеження двоїстої пари повинен відповідати напрямку цільової функції. Типічним представником такої пари є транспортна задача.