50.Автокореляція: зміст, причини виникнення та її наслідки.

При дослідженні динамічних процесів, тобто явищ, яких за часом і у просторі виникає необхідність розглядати взаємозв’язок спосте-режень у різні моменти часу поведінки об’єк-ту.(Вплив обсягів капітальних вкладень на майбутні обсяги виробництва готової прод-ії). Залежність між послідовними залишками множини спостережень однієї вибірки через деякий час періоду досліджень називають автокореляцією. Таке явище присутнє для однієї тієї ж вибірки. Якщо зустрічаються різні вибірки 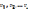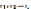то у цьому випадку відсутня автокореляція і для цих різних вибірок існує серійна кореляція. При наявності явища автокореляції, кореля-ційна залежність можна записати так: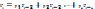 де - коефіцієнт автокореляції випадкової величи-ни за нормальним законом розподілу Якщо має місце взаємозв’язок між сусідніми члена-ми часового ряду, то таке явище називається автокореляція І-го порядку, яке має вигляд 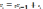де - випадкова величина за нормальним законом розподілу Автокореля-ція залишків є значною проблемою в процесі дослідження динамічних рядів: 1.помилковий вибір специфікації економетричної моделі 2. значні помилки в вихідному масиві спостере-жень 3. інертність та циклічність явища дослі-дження 4. відсутність змінних, які не увійшли до економетричної моделі і значно впливають на її вибір Якщо не враховувати явище авто-кореляції залишків, то при будуванні еконо-метричної моделі за допомогою МНК може статися таке: 1.оцінка параметрів теоретичної залежності може бути не змішенними, але неефективними при значній величині диспе-рсії оцінок параметрів. 2.неможливість вико-ристовувати статистичний критерій Студента та Фішера 3.аналіз поведінки економетричної моделі буде неефективним, тобто має місце процес прогнозування з великою величиною вибіркової дисперсії. У випадках існування автокореляції залишків необхідно будувати спеціальну матрицю S, яка є матрицею коефіцієнтів автокореляції залишків. Матри-ця вводиться для коригування вихідних да-них. Загальний вигляд цієї матриці такий:

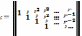
да р – коефіцієнти кореляції, які знаходяться за допомогою величин залишків. Така матри-ця є симетричною і називається коваріаціон-ною матрицею залишків і використовується для знаходження параметрів при наявності явища автокореляції. Коефіцієнти авто коре-ляції р назив. циклічним і знаходяться у діапазоні [-1;1]. Якщо необхідно до викорис-тання МНК, тобто до класичної залежності економетричної моделі, то в матриці S треба прийняти р=0, тобто таким чином одержуючи одиничні матриці

51.Методи визначення автокореляції.

Для визначення явища автокореляції викори-стовують критерій Дарвіна – Уотсона, крите-рій Фон Неймана,  коефіцієнт автокореляції (циклічний коефіцієнт). Загальна процедура аналізу явища автокореляції:

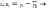
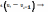
Для використання критерію для аналізу на автокореляцію необхідно підготувати загальні проміжні величини, які знаходяться в блоках 1-4: 1.Необхідно знайти теоретичну залежні-сть МНК 2. – 4. Знаходяться проміжні дані, які відносяться до залишків вихідних величин Після використання І частини проводиться аналіз по конкретним критеріям5. – 6. Прово-диться аналіз на автокореляцію за допомогою критерія Дарвіна – Уотсона. Цей критерій використовується для малих сукупностей вихідних даних. Іноді якщо відомі коеф. автокореляції, то величини цього артерія можливо знаходиться так: DW = 2p – p значення цього критерія знаходиться у діапа-зоні (0;4). Якщо залишки не автокорельовані (тобто коли р = 1), то значення величин DW знах. поблизу величини 2. Якщо критерій DW знах. у діапазоні (0;2), то має місце додатня автокореляція. Якщо величина DW знаходи-ться у діапазоні (244), то має місце від’ємна автокореляція. Фактичне значення величини DW порівнюється з табличним, для n спосте-режень. В статистичній таблиці наводиться нижня межа 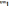та верхня 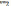. Якщо вели-чина > DW автокореляція відсутня. Якщо DW у діапазоні (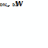 ), то не можливо дати однозначний висновок, тобто необхідно додаткове дослідження для збільшення сукупності спостереження. Якщо коефіцієнт кореляції р = 1, то DW = 0. Якщо р = 0, то DW = 2. Якщо р = -1, то DW = 4. Критерій Фон Неймана Після підготовки вихідних даних проводиться аналіз на автокореляцію за схемою: 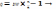; . У випадку, коли за критерієм Дарвіна не можливо виявити існування автокореляції використовують критерій Фон Неймана. Він фактично критерієм коригування критерія Дарвіна. Для одержаного значення критерія знаходять табличне значення для α = 0,05 та кількості n. В таблиці цього критерія наводя-ться 2 стовпця для додатної автокореляції та відємної. Якщо то існує додатня автокореляція. Критерій по циклічному коефіцієнту.

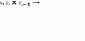
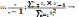
9. – 10. Знаходження фактичного значення циклічного коефіцієнта автокореляції, який знаходиться у діапазоні (-1;1). Згідно зі значеннями α та n знаходження табл. значення цього коефіцієнта. Якщо фактичне значення більше табличного, то має місце автокореляція.

49.Визначення діагональної матриці в методі Ейткена Якщо в економічній моделі має місце гетероскедастичність, то для оцінки параметрів теоретичної залежності не доцільно використовувати МНК. Для такої моделі розроблено спеціально узагальнений метод Ейткена. Різниця між МНК і УМНК така: за допомогою МНК параметри моделі знаходяться за допомогою мінімізації квадра-тів відхилення фактичного теоретичного зна-чення показника 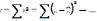. В УМНК цільова функція передбачає наступний вигляд: де - вагові коефіцієнти На практиці часто такі коефіцієнти залежать від дисперсії 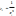тобто в УМНК мінімізується зважена сума квадратних відхилень В цьому методі знахо-диться параметри моделі, ведеться з викорис-танням додаткової визначеної матриці S, яка є симетричною і коригує вихідну інформацію пом’якшуючи явище гетероскедастичності. В додатковій матриці S елементи , які є діагональними вибираються за одною із гіпо-тез:1. дисперсія залишків пропорційна обер-неній величині змінних , тобто 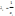2. дисперсія залишків пропорційна оберненій величині квадрату змінної 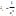3. дис.-персія залишків пропорційна до змін квад-рату залишків за модулем 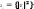. Зага-льний вигляд додат. матриці S має форму:

тобто ця матриця є додатною симетричною матрицею В УМНК параметри теоретичної залежності мають наступну матричну форму 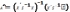після одержаних параметрів теоретичної залежності з урахува-нням додаткової матриці S проводиться ана-логічний аналіз на адекватність, як і в МНК, тобто знаходиться коефіцієнт кореляції, квад-рати залишків та використовується стат. коеф.