25.Задача про найкоротшу відстань: модель та алгоритм.

Задача про найкоротшу відстань є типовою транспортною задачею у сітьовій постановці. Вона об’єднує не тільки клас транспортних за-дач, до неї можна звести низку прикладних виробничих задач:1)про зміну обладнання; 2)знаходження найнадійнішого маршруту; 3)про мінімізацію аварійних ситуацій; 4)прое-ктування та ін. Щоб розв’язати задачу у сітьо-вій постановці треба знати топологію сітки та величини пропускних спроможностей S_ij. Мат. 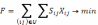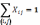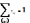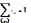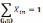модель цієї задачі має такий вигляд: цільова функція: ; Обмеження: – початковий пункт; – кінцевий пункт; 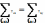для 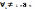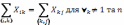. Таку модель можна розв’язати симплекс-методом, але для сітьо-вих задач розроблено простіші методи розв’я-зування, тому не доцільно для таких задач використовувати симплекс метод. Алгоритм розв’язування:обчислювальна процедура роз-в’язування задачі розглядається для мережі без циклів і з однією початковою S та кінце-вою t вершинам. Заздалегідь усі вершини I графа G мають бути упорядковані, тобто про-нумеровані згідно з напрямом дуг з ліва на право. Кожна дуга повинна мати оцінку d_ij – відстань від i-ї до j-ї вершини. Алгоритм знаходження найкоротшої відстані від S до t такий. 1.Розбиття множини вершин I на дві підмножини SUS’ = I. Первісно у множину S входить тільки одна вершина: i=I, тобто джерело S.

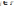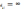
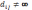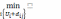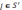2.Вибір вершини в і знаходже-ння оцінки .3.Закріплення за j-ю вершиною оцінки U_i. 4. Переведення j-ї вер-шини з підмножини S’ у підмножину S та привласнення їй наступного номера i. 5. Пере-хід до наступної вершини . 6. Перевірка чи всі вершини переглянуто, тобто, чи дійшов процес розв’язання до вершини t. Якщо так то перехід до п. 7, якщо ні то перехід до п. 2. 7. Знаходження найкоротшої відстані L=U_t та будування найкоротшого шляху {(ij)}.

26.Загальна економетрична модель та її постановка.

При дослідженні економічних процесів часто виникає необхідність провести аналіз взаємо-зв’язків між декількома показниками та вста-новити між ними тісноту зв’язків, які не мають строгих функціональних залежностей. Така проблема вирішується за допомогою будування моделей, які передбачають зв’язки між незалежними та результативними показ-никами.Такі задачі відносяться до дисциплін-ни «Економетрія», за допомогою інструмент-тарія якої будується економетрична модель процесу.Для економетричної задачі характер-ною особливістю є те, що для кожної незале-жної змінної х_і може існувати декілька залеж-них величин у_і, які називаються результатив-ними показниками. Це обумовлюється тим, що існують помилки в величинах х_і, а також існують ситуації, коли не враховуються декот-рі суттєві величини х_і, які називають фактора-ми.Для розв’язання теких задач використову-ють статистичні дані, за якими знаходять емпіричні залежності. Для цього використо-вують апарат теорії ймовірності, математич-ної статистики, особливо регресійно-кореля-ційний аналіз. На цій базі розробляють стати-стичні методи, за якими будують економетри-чну модель, яка пов’язує результативний по-казник з множиною незалежних факторів. В результаті такого процесу економічне явище описується рівнянням регресії, яка носить статистичних характер. Це обумовлено тим, що в статистичних даних має місце помилки виміру або невраховані фактори. Величину помилки позначають u_i і називають похиб-кою.Змістова постановка економетричної за-дачі наступна: знайти параметри теоретичної залежності Уˆ=АˆХ, А=||a_i|| для фактично заданих залежних і незалежних величин у вигляді У=АХ+u, при яких цільова функція приймає мінімальне значення F=∑u_i²=∑(y_iˆ-y_i)²->min, де Х – матриця незалежних змінних х_і, Х=||x_i||, У – матриця фактичних значень залежної змінної, Уˆ- матриця теоретичних значень залежної змінної,Аˆ - матриця теоре-тичних значень параметрів рівняння регресії, u – матриця фактичних похибок. Необхідною умовою одержання мінімума значення F є обернення її частинних похідних в нуль, тобто необхідно розв’зати систему нормальних рівнянь ∂F/∂a₀=0; ∂F/∂a₁=0;… ∂F/∂a_n=0. В результаті розв’язання такої системи знаходя-ться параметри а₀, а₁, … , а_п, які складають мат-рицю параметрів А. Коефіцієнти а_і назв коеф. регресії або параметрами , які показують на скільки одиниць у середньому змінюється результативна величина у_і, якщо і-й фактор зміниться на 1, при умові, що усі інші фактори залишаться на постійному рівні. Загальний підхід до розв’язування таких задач можливо вести за допомогою розв’язування системи нормальних рівнянь методом найменших квадратів. Цей метод забезепечує мінімізував-ня середньоквадратичної помилки при знахо-дженні параметра економетричної моделі. Для розв’язання економетричної задачі доці-льно використовувати матричний спосіб як для парної так і для множинної регресії.