1.Загальна задача лінійного програмування.

Якщо задача має множину розв’язків то необхідно з цієї множини знайти найкращий варіант з цієї множини з точки зору мети. Такі задачі називаються – задачами оптимізації, а найкращий варіант оптимальним. Щоб знайти оптимальний варіант треба перейти від змістової постановки задачи до марема-тичної такий процес називається математич-ним моделюванням. В результаті такого моделювання складається математична модель. Загальний зміст математичної моделі: Необхідно знайти множину змін Х1, Х2…Хn Xj(j=1,n) при яких задана цільова функція приймає екстремальне значення: 1)F=f(Xj) ext(max,min), при виконанні обмежень виробничого характеру.

2);

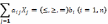
3)при зміні величини 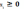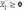або численні. Для задач оптимізації розроблені моделі та алгоритми розв’язання, які класифікуються згідно з поведінкою цільової функції та обмеження моделі.

2.Графічний метод розв’язування злп.

Цей методи використовується для двомірних задач або задач в яких виконується умова n-m<2 з наступними перетвореннями. Процес розв’язування задач графічним методом складається з 2-х етапів: 1)Згідно з обмеженням будується область допустимих розв’язків де знаходиться множина розв’язків. При будуванні області допустимих розв’язків існує 3 випадки: 1.Область у вигляді випуклої фігури:У цьому випадку існує min і max цільової функції.

2.Область допустимих розв’язків не обмежена з одного боку:

У цьому випадку задача або min або max, або не має розв’язків. 3.Області допустимих розв’язків не існує

2)Знаходження оптимального варіанту, для цього використовується властивості градієнту цільової функції. Алгоритм розв’язування: 1.Згідно з обмеженням будується область допустимих розв’язків. Для цього по кожному обмеженню будується його допустима полуплощина. Щоб побудувати полуплощину необхідно дане обмеження задати у виді рівняння, а потім побудувати її в невідємнії частині. Щоб знайти допустиму полуплощину необхідно взяти будь-яку точку з координат та підставити її в обмеження. Якщо знак обме-ження не порушується, то дана точка знахо-диться в допустимій полуплощині. Перетин усіх допустимих полуплощин відповідає загальній області допустимих розв’язків. 2.Бу-дування градієнту цільової функції. Градієнт проходить через початок координат та точку координати якої є оцінюючий коефіцієнт Cj. 3.Будування прямої цільової функції. Така пряма будується перпендикулярно градієнту в будь-якої точці. 4.Знаходження оптимальної точки. Для цього пряма цільової функції з совується по напряму градієнту наближуючи-сь до області допустимих розв’язків. Найбли-жча точка дотику прямої цільової функції з областю відповідає min значенню цільової ф-ії. Найдальша точка відповідає max цільової ф-ії. 5.Для знаход-ження оптимального зна-чення цільової ф-ії складається система рівнянь до якої входить 2-і прямі які утворюють знайдену оптимальну точку.

5.Альтернативний оптимум в ЗЛП При вирішенні задач ЛП симплексним методом критерієм оптимальності є умова Δj> 0 для задач на максимум і умова Δj <0 для задач на мінімум. Якщо на якомусь кроці виявиться, що хоча б одна оцінка вільної змінної Δj = 0, а всі інші Δj> 0 для задач на максимум (Δj <0 для задач на мінімум), то, прийнявши в якості ключового стовпця стовпець , де Δj = 0, і, знайшовши нове оптимальне рішення, зауважимо, що значення цільової функції при цьому не зміниться. У цьому випадку завдання має альтернативний оптимум. Критерієм альтернативного оптимуму при вирішенні завдань симплексним методом є рівність нулю хоча б однієї оцінки вільної змінної (Δj = 0). Якщо тільки одна оцінка вільної змінної дорівнює нулю, то рішення знаходиться за формулою X*опт = tX*опт1 + (1 - t)X*опт2, де 0 <t<1. Якщо дві оцінки і більше, наприклад S, вільних змінних дорівнюють нулю, то оптимальне рішення визначається за формулою X*опт = t1X*1 + t2X*2 + ... + tsX*s, де t1 + t2 + ... + ts = 1, ti>0. У завданнях, що мають альтернативний оптимум, виникає можливість включення до її модель інших критеріїв ефективності.