
- •Билет 3 Понятие предела Геометрический смысл предела
- •Билет4 Бесконечно малая и бесконечно большая
- •Бесконечно большая величина
- •Свойства бесконечно малых
- •Сравнение бесконечно малых Определения
- •Примеры сравнения
- •Понятие о непрерывности функции.
- •Максимум и минимум функции.
- •Билет 15
- •Правила дифференцирования
- •Дифференцирование сложной и обратной функций
- •2. Нахождение асимптоты
- •Тейлора формула
- •Доказательство Отношение бесконечно малых
- •Отношение бесконечно больших
- •Примеры
2. Нахождение асимптоты
Пусть функция f (x) определена для всех x а (соответственно для всех
x а). Если существуют такие числа k и l, что f(x) kx l = 0 при х (соответственно при х ), то прямая
y = kx + l
называется асимптотой графика функции f (x) при x (соответственно при х ).
Существование асимптоты графика функции означает, что при х +
(или х ) функция ведёт себя «почти как линейная функция», то есть отличается от линейной функции на бесконечно малую.
 x
x![]()
3x
2
3x
2
Найдём, например, асимптоту графика функции y = x 1
Разделив числитель на знаменатель по правилу деления многочленов,
 2 2
2 2
получим y = x 4 + x + 1 Так как x + 1 = 0 при х , то прямая y = x-4
является асимптотой графика данной функции как при х + ,
так и при х .
Билет 18 точки перегиба функции
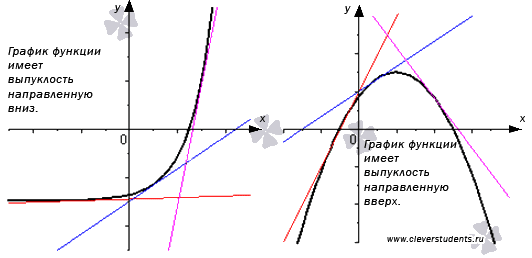
Определения и понятия. Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х. Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х. Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой. Посмотрите на чертеж, иллюстрирующий эти определения.
Точка ![]() называется точкой
перегиба графика функции y
= f(x),
если в данной точке существует касательная
к графику функции (она может быть
параллельна оси Оу)
и существует такая окрестность точки
называется точкой
перегиба графика функции y
= f(x),
если в данной точке существует касательная
к графику функции (она может быть
параллельна оси Оу)
и существует такая окрестность точки ![]() ,
в пределах которой слева и справа от
точки М график
функции имеет разные направления
выпуклости.
Другими словами,
точка М называется
точкой перегиба графика функции, если
в этой точке существует касательная и
график функции меняет направление
выпуклости, проходя через нее.
Если
необходимо, обратитесь к разделу касательная
к графику функции в точке,
чтобы вспомнить условия существования
невертикальной и вертикальной
касательной.
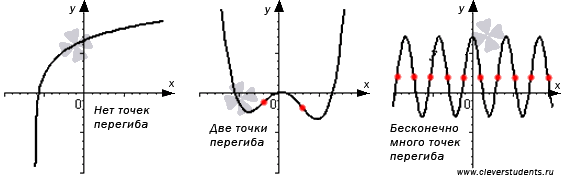
На рисунке ниже
представлены несколько примеров точек
перегиба (отмечены красными точками).
Заметим, что некоторые функции могут
не иметь точек перегиба, а другие могут
иметь одну, несколько или бесконечно
много точек перегиба.
,
в пределах которой слева и справа от
точки М график
функции имеет разные направления
выпуклости.
Другими словами,
точка М называется
точкой перегиба графика функции, если
в этой точке существует касательная и
график функции меняет направление
выпуклости, проходя через нее.
Если
необходимо, обратитесь к разделу касательная
к графику функции в точке,
чтобы вспомнить условия существования
невертикальной и вертикальной
касательной.
На рисунке ниже
представлены несколько примеров точек
перегиба (отмечены красными точками).
Заметим, что некоторые функции могут
не иметь точек перегиба, а другие могут
иметь одну, несколько или бесконечно
много точек перегиба.
Нахождение интервалов выпуклости функции.
Сформулируем
теорему, которая позволяет определять
промежутки выпуклости функции.
Если
функция y
= f(x) имеет
конечную вторую производную на
интервале Х и
если выполняется неравенство ![]() (
(![]() ),
то график функции имеет выпуклость
направленную вниз (вверх) на Х.
Эта
теорема позволяет находитьть промежутки
вогнутости и выпуклости функции, нужно
лишь на области определения исходной
функции решить неравенства
),
то график функции имеет выпуклость
направленную вниз (вверх) на Х.
Эта
теорема позволяет находитьть промежутки
вогнутости и выпуклости функции, нужно
лишь на области определения исходной
функции решить неравенства ![]() и
и ![]() соответственно.
Следует
отметить, что точки, в которых функция y
= f(x) определена,
а вторая производная не существует,
будем включать в интервалы вогнутости
и выпуклости.
соответственно.
Следует
отметить, что точки, в которых функция y
= f(x) определена,
а вторая производная не существует,
будем включать в интервалы вогнутости
и выпуклости.
Билет 19 формула тейлора
