Дифференцирование сложной и обратной функций
Приведем правило по которому можно найти производную сложной функции y = f((t)).
Теорема 3 (дифференцирование сложной функции). Пусть функция x = (t) дифференцируема в точке t, а функция y = f(x) дифференцируема в соответствующей точке x = (t). Тогда сложная функция y = f((t)) дифференцируема в точке t, причем справедлива формула
(f((t)))' = f'(x)'(t). |
(3) |
Доказательство. Зададим x = (t) отличное от нуля приращение t. Этому приращению отвечает приращение x = (t+ t)- (t) функции x = (t). Приращению x отвечает приращение y = f(x+ x)-f(x). Так как функция y = f(x)дифференцируема, то ее приращение y представимо в виде (1):
y =f'(x) x + ( x) x,
где lim x 0 ( x ) = 0. Поделив данное выражение на t 0, будем иметь:
y/ t=f'(x) x/ t+ ( x) x/ t.
Из дифференцируемости функции x = (t) в точке t вытекает, что
lim t 0 x/ t = '(t).
Отметим, что из дифференцируемости функции x = (t) следует, что x 0 при t 0. Следовательно, lim t 0 ( x) =0. Таким образом, получим необходимую формулу (3).
Пример 5. Найти y', если y = 5cos x.
y' = 5cos x(-sin x)ln 5=-5cos x sin x ln 5.
Для нахождения производной обратной функции существует следующее правило, а именно справедлива теорема
Билет 16 Необходимое и достаточное условия возрастания функции
(Необходимое и достаточное условия возрастания функции)
Если дифференцируемая функция y=f(x) возрастает на [a, b], то ее производная неотрицательна на этом отрезке, f '(x)≥ 0.
Обратно. Если функция y=f(x) непрерывна на [a, b], дифференцируема на (a, b) и ее производная положительна на этом отрезке,f ' (x)≥ 0 для a<x<b, то f(x)возрастает на[a, b].
Доказательство.
Докажем первую часть теоремы. Итак, пусть функция y=f(x) возрастает на [a, b]. Зафиксируем на этом отрезке произвольную точку x, придадим ей приращение Δx. Тогда если Δx>0, то x<x+Δx. Поэтому по определению возрастающей функции f(x)<f(x+Δx), то есть f(x+Δx) - f(x)>0. Но тогда и
Аналогично,
если Δx<0, то x>x+Δx и
значит f(x+Δx)-f(x)<0, а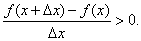 
Переходя
в этом равенстве к пределу при
Δx→0, получим 
,
то есть f
'(x)≥0.
Докажем вторую часть теоремы. Пусть f '(x)>0при всех x (a,b). Рассмотрим два любых значения x1 и x2 таких, что x1 < x2. Нужно доказать, что f(x1)< f(x2). По теореме Лагранжа существует такое число c (x1, x2), что
.
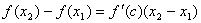По условию f
'(x)>0, x1 – x2>0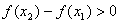 
,
а это и значит, что f(x) –
возрастающая функция.
Аналогичная теорема имеет место и для убывающих функций.
-
Теорема 2. Если f(x) убывает на[a,b], то
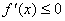на
этом отрезке. Если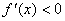 
на
(a;
b),
то f(x) убывает
на [a,
b],в
предположении, чтоf(x) непрерывна
на [a,
b].Доказанная теорема выражает очевидный геометрический факт. Если на [a, b] функция возрастает, то касательная к кривой y=f(x) в каждой точке этого отрезке образует острый угол с осью Ox или горизонтальна, т.е. tga≥0, а значит f '(x)≥0.
Аналогично иллюстрируется и вторая часть теоремы.
Таким образом, возрастание и убывание функции характеризуется знаком ее производной. Чтобы найти на каком промежутке функция возрастает или убывает, нужно определить, где производная этой функции только положительна или только отрицательна, то есть решить неравенства f '(x)>0 – для возрастания или f '(x)<0 – для убывания.
Примеры. Определить интервалы монотонности функции.
.
Область определения заданной
функции D(y) =
(-∞; 0)(0;
+∞).
.
Следовательно, f(x) –
убывает на (-∞; 0) и (0; +∞).Найдем промежутки, на которых производная заданной функции положительна или отрицательна методом интервалов.
Итак, f(x) – убывает на (–∞; –1] и [1; +∞), возрастает на отрезке [–1; 1].
.
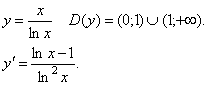Используя метод интервалов, получим f(x) убывает на (0; 1) и (1; e], возрастает на [e; +∞).
Билет 17 понятие асимптот графика функции и их нахождение
Асимптота, так называемая прямая или кривая линия, которая, будучи продолжена, приближается к другой кривой, но никогда не пересекает ее, так что расстояние между ними делается бесконечно малой величиной.
Понятие асимптоты играет важную роль в математическом анализе. Они проводятся при изучении свойств многих кривых (гиперболы, конхоиды, логарифмич. линии, циссоиды и др.).