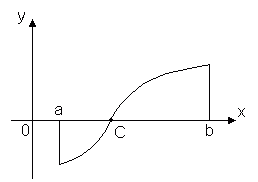Понятие о непрерывности функции.

Определение:  Функция f(x) называется непрерывной в точке а, если при стремлении х к а значение f(x) стремится к значению f(a).  Это означает, что для любого числа   существует такое число  , что для всех х,удовлетворяющих неравенству   выполняется неравенство  . Пример.  Докажем, что линейная функция  непрерывна в любой точке а.  

Графическая иллюстрация.

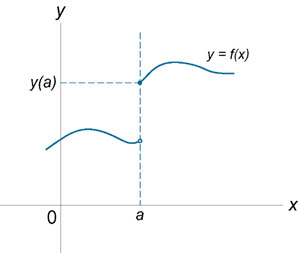
График непрерывной функции представляет собой непрерывную кривую. На рисунках видно, в чём состоит различие между графиком непрерывной функции и графиком так называемой, разрывной функции, которая не является непрерывной.

Билет 8 классификация точек разрыва функции

Точки разрыва функции

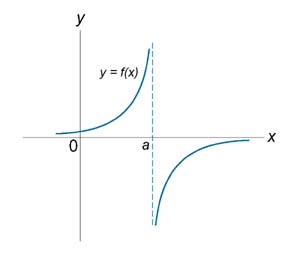
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв. Непрерывна при x = a. Имеет разрыв при x = a. Непрерывна при x = a. Имеет разрыв при x = a. Рисунок 1. Классификация точек разрыва функции Все точки разрыва функции разделяются на точки разрыва первого и второго рода.  Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке Существуют левосторонний предел   и правосторонний предел  ; Эти односторонние пределы конечны. При этом возможно следующие два случая: Левосторонний предел и правосторонний предел равны друг другу: Такая точка называется точкой устранимого разрыва. Левосторонний предел и правосторонний предел не равны друг другу: Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов  называется скачком функции. Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.

Билет 9 теоремы о непрерывных функциях. теорема коши. теорема вейерштрасса

СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ

Рассмотрим некоторые свойства функций непрерывных на отрезке. Эти свойства приведём без доказательства.

Функцию y = f(x) называют непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b, непрерывна соответственно справа и слева.

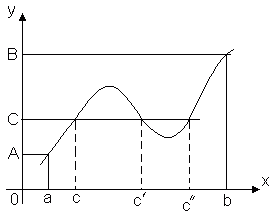
Теорема 1. Функция, непрерывная на отрезке [a, b], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.

Т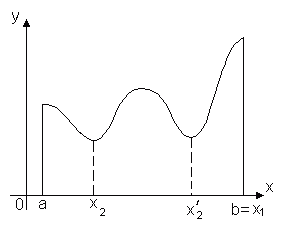 еорема утверждает, что если функция y = f(x) непрерывна на отрезке [a, b], то найдётся хотя бы одна точка x₁  [a, b] такая, что значение функции f(x)в этой точке будет самым большим из всех ее значений на этом отрезке: f(x₁) ≥ f(x). Аналогично найдётся такая точка x₂, в которой значение функции будет самым маленьким из всех значений на отрезке: f(x₁) ≤ f(x).

Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x₂ и x₂'.

Замечание. Утверждение теоремы можно стать неверным, если рассмотреть значение функции на интервале (a, b). Действительно, если рассмотреть функцию y = x на (0, 2), то она непрерывна на этом интервале, но не достигает в нём ни наибольшего, ни наименьшего значений: она достигает этих значений на концах интервала, но концы не принадлежат нашей области.

Также теорема перестаёт быть верной для разрывных функций. Приведите пример.

Следствие. Если функция f(x) непрерывна на [a, b], то она ограничена на этом отрезке.

Теорема 2. Пусть функция y = f(x) непрерывна на отрезке [a, b] и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка [a, b] найдется, по крайней мере, одна точка x = C, в которой функция обращается в ноль: f(C) = 0, где a < C< b Эта теорема имеет простой геометрический смысл: если точки графика непрерывной функции y = f(x), соответствующие концам отрезка [a, b] лежат по разные стороны от оси Ox, то этот график хотя бы в одной точке отрезка пересекает ось Ox. Разрывные функции этим свойством могут не обладать. Эта теорема допускает следующее обобщение. Теорема 3 (теорема о промежуточных значениях). Пусть функцияy = f(x) непрерывна на отрезке [a, b] и f(a) = A, f(b) = B. Тогда для любого числа C, заключённого между A и B, найдётся внутри этого отрезка такая точка CÎ [a, b], что f(c) = C. Эта теорема геометрически очевидна. Рассмотрим график функции y = f(x). Пусть f(a) = A, f(b) = B. Тогда любая прямая y = C, где C – любое число, заключённое между A и B, пересечёт график функции, по крайней мере, в одной точке. Абсцисса точки пересечения и будет тем значением x = C, при котором f(c) = C. Таким образом, непрерывная функция, переходя от одного своего значения к другому, обязательно проходит через все промежуточные значения. В частности: Следствие. Если функция y = f(x) непрерывна на некотором интервале и принимает наибольшее и наименьшее значения, то на этом интервале она принимает, по крайней мере, один раз любое значение, заключённое между её наименьшим и наибольшим значениями.

Теоре́ма Больца́но — Коши́ о промежуточных значениях непрерывной функции в математическом анализе и общей топологии — это утверждение о том, что если непрерывная функция принимает два значения, то она принимает и любое значение между ними.

[править]Формулировка

Пусть дана непрерывная функция на отрезке   Пусть также   и без ограничения общности предположим, что   Тогда для любого   существует   такое, что  .

Доказательство  [показать]

[править]Следствия

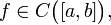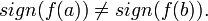• (Теорема о нуле непрерывной функции.) Если функция на концах отрезка принимает значения противоположных знаков, то существует точка, в которой она равна нулю. Формально: пусть   и   Тогда 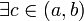  такое, что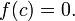 

• В частности любой многочлен нечётной степени имеет по меньшей мере один нуль.

[править]Замечание

• Иногда (в учебных курсах) утверждение для нуля называется первой теоремой Больцано — Коши, а общее утверждение — второй теоремой соответственно^[1]. На самом деле они эквивалентны.

[править]Обобщение

Теорема Больцано — Коши допускает обобщение на более общие топологические пространства. Всякая непрерывная функция  , определенная на связном топологическом пространстве, принимающая какие-либо два значения, принимает и любое лежащее между ними. Формальная запись: пусть дано связное топологическое пространство   и функция   Пусть   и   Тогда

В такой формулировке теорема является частным случаем теоремы о том, что образ связного множества при непрерывном отображении связен.

Первая и вторая теорема Вейерштрасса Теорема (первая теорема Вейерштрасса) Если функция непрерывна на сегменте, то она ограничена на нем. Доказательство: методом от противного, воспользуемся свойством замкнутости сегмента [a;b]. Из любой последовательности (xn) этого сегмента можем выделить подпоследовательность xnk, сходящуюся к x0∈[a;b]. Пусть f не ограничена на сегменте [a;b], например, сверху, тогда для всякого натуральногоn∈Nнайдется точка xn∈[a;b], что f(xn)>n. Придавая n значения 1,2,3,{\ldots}, мы получим последовательность (xn) точек сегмента [a;b], для которых выполнено свойствоf(x1)>1,f(x2)>2,f(x3)>3,...,f(xn)>n... Последовательность (xn) ограничена и поэтому из нее по теореме можно выделить подпоследовательность(xnk), которая сходится к точке x0∈[a;b]: limk→∞xnk=x0 (1) Рассмотрим соответствующую последовательность (f(xnk)). С одной стороны f(xnk)>nk и поэтомуlimk→∞f(xnk)=+∞ (2), С другой стороны, учитывая определение непрерывной функции по Гейне из (1) будем иметьlimk→∞f(xnk)=f(x0) (3) Получаем равенства (2) и (3) противоречат теореме (о единственности предела). Это противоречие и доказывает справедливость теоремы. Аналогично доказывается ограниченность функции снизу. Ч.Т.Д.

Замечание 1 Таким образом, если f непрерывна на [a;b], то ее множество значений ограничено и поэтому существует конечные верхняя и нижняя грань функции. c=infx∈[a;b]f(x),d=supx∈[a;b]f(x), но открыт вопрос о достижении  функции своих граней. Замечание 2 Если слово сегмент в условии теоремы заменить словом интервал или полуинтервал, то теорема может и нарушиться. Пример, y=tgx,tgx∈C((−2π;2π)), но функция не ограничена на этом интервале.

  Теорема (вторая теорема Вейерштрасса) Если функция непрерывна на сегменте, то она достигает на нем своих граней (т.е. непрерывная на сегменте функция принимает свое наибольшее и наименьшее значения). Доказательство: Пусть f(x)∈C([a;b]), c=infx∈[a;b]f(x), d=supx∈[a;b]f(x). По первой  теореме Вейерштрасса c,d∈R. Докажем, что f достигает на [a;b] своих граней, т.е. найдутся такие точкиx1,x2∈[a;b], чтоf(x1)=c,f(x2)=d. Докажем, например, существование точки x2.

По определению верхней грани имеем (∀x∈[a;b])(f(x)=d). Предположим противное, т.е. точки x2, в которой f(x2)=dна [a;b], тогда на [a;b] выполняется условиеf(x)<d или d−f(x)>0. Далее введем вспомогательную функцию ϕ(x)=1d−f(x) . ϕ(x) на [a;b] положительна и непрерывна (как отношение двух непрерывных на [a;b] функций и d−f(x)/=0) , поэтому по первой Т. Вейерштрасса ϕ(x) на [a;b]ограничена.  Это означает, что при некотором М>0 (∀x∈[a;b])(0<1d−f(x)≤M), отсюда имеем f(x)≤d−1M<d.  Полученное неравенство противоречит тому, что d является верхней гранью функции f(x) на [a;b], т.е. наименьшим из верхних границ. Полученное противоречие и означает существование точки x2 такой, чтоf(x2)=d.

Аналогично доказывается существование точки x1∈[a;b], такой что f(x1)=c.

Следствие Если f непрерывна и непостоянна на [a;b], то образ этого отрезка [a;b] при отображении f будет так же отрезок, т.е. непрерывный непостоянный образ отрезка есть отрезок. Доказательство: В самом деле образом отрезка [a;b] при отображении f будет отрезок [с;d], где c=inf[a;b]f(x)=min[a;b]f(x), а d=sup[a;b]f(x)=max[a;b]f(x), что следует из второй теоремы Больцано-Коши и второй теоремы Вейерштрасса Ч.Т.Д.

Билет 10. Опредение производной

Определение производной функции в точке.Пусть функция f(x) определена на промежутке (a; b),   и   - точки этого промежутка.Производной функции f(x) в точке   называется предел отношения приращения функции к приращению аргумента при  . Обозначается  .

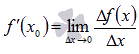Когда последний предел принимает конкретное конечное значение, то говорят о существовании конечной производной в точке. Если предел бесконечен, то говорят, чтопроизводная бесконечна в данной точке. Если же предел не существует, то и производная функции в этой точке не существует.Функцию f(x) называют дифференцируемой в точке  , когда она имеет в ней конечную производную.Если функция f(x) дифференцируема в каждой точке некоторого промежутка (a; b), то функцию называют дифференцируемой на этом промежутке. Таким образом, любой точке x из промежутка (a; b) можно поставить в соответствие значение производной функции в этой точке  , то есть, мы имеем возможность определить новую функцию  , которую называют производной функции f(x) на интервале (a; b).

Операция нахождения производной называется дифференцированием.Проведем разграничения в природе понятий производной функции в точке и на промежутке: производная функции в точке – это есть число, а производная функции на промежутке – это есть функция.Давайте разберем это на примерах для ясности картины. При дифференцировании будем пользоваться определением производной, то есть переходить к нахождению пределов. При возникновении трудностей рекомендуем обращаться к разделу теории пределы, основные определения, примеры нахождения, задачи и подробные решения.

Пример.Найти производную функции   в точке  , используя определение.

Решение.

Так как мы ищем производную функции в точке, то в ответе должно быть число. Запишем предел отношения приращения функции к приращению аргумента и воспользуемся формулами тригонометрии:

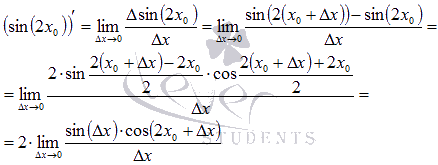
Осталось применить первый замечательный предел для получения конечного результата:

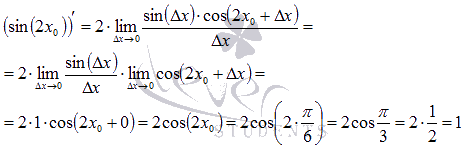
Ответ:

Билет 12 уравнение касательной к графику функции. Вывод уравнения.

Касательной к графику функции y = f(x) в точке   называют прямую, проходящую через точку  , с отрезком которой практически сливается график функции при значениях х сколь угодно близких к  . Поясним это определение на примере. Покажем, что прямая y = x+1 является касательной к графику функции   в точке (1; 2). Для этого покажем графики этих функций при приближении к точке касания (1; 2). Черным цветом показан график функции  , касательная прямая показана синей линией, точка касания изображена красной точкой. Каждый последующий рисунок является увеличенной областью предыдущего (эти области выделены красными квадратами).

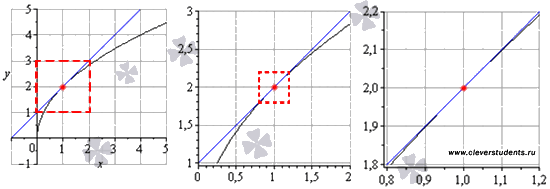
Хорошо видно, что вблизи точки касания график функции   практически сливается с касательной прямой y = x+1.  А сейчас перейдем к более значимому определению касательной. Для этого покажем, что будет происходить с секущей АВ, если точку В бесконечно приближать к точке А. Рисунок ниже иллюстрирует этот процесс.

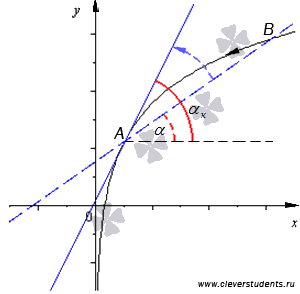
Секущая АВ (показана синей пунктирной прямой) будет стремиться занять положение касательной прямой (показана синей сплошной линией), угол наклона секущей   (показан красной прерывистой дугой) будет стремиться к углу наклона касательной   (изображен красной сплошной дугой). Таким образом, касательная к графику функции y = f(x) в точке А – это предельное положение секущей ABпри  . Вот теперь можно переходить к оописанию геометрического смысла производной функции в точке.  Алгоритм составления уравнения касательной к графику функции y = f(x)

1. Обозначить буквой a абсциссу точки касания. 2. Найти f(a). 3. Найти f '(x) и f '(a). 4. Подставить найденные числа a, f(a), f '(a) в общее уравнение касательной y = f(a) = f '(a)(x – a).

Этот алгоритм может быть составлен на основе самостоятельного выделения учащимися операций и последовательности их выполнения.

Билет 13. определение возрастающей и убывающей функции

Определение возрастающей функции. Функция y = f(x) возрастает на интервале X, если для любых   и   выполняется неравенство  . Другими словами – большему значению аргумента соответствует большее значение функции. Определение убывающей функции. Функция y = f(x) убывает на интервале X, если для любых   и   выполняется неравенство  . Другими словами – большему значению аргумента соответствует меньшее значение функции.

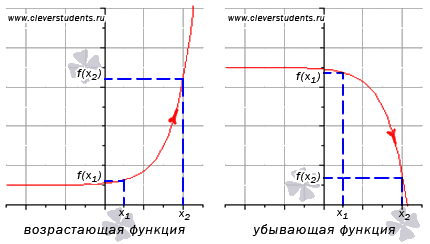
ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания (a; b), то есть при x = a и x = b, то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X. К примеру, из свойств основных элементарных функций мы знаем, что y = sinx определена и непрерывна для всех действительных значений аргумента. Поэтому, из возрастания функции синуса на интервале   мы можем утверждать о возрастании на отрезке  . Точку   называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство  . Значение функции в точке максимума называют максимумом функции и обозначают  . Точку   называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают  . Под окрестностью точки   понимают интервал  , где   - достаточно малое положительное число.  Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.

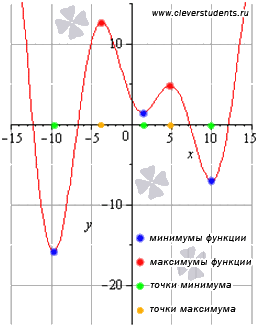
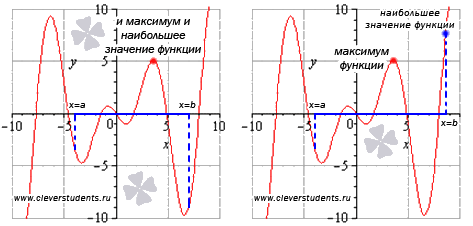
Не путайте экстремумы функции с наибольшим и наименьшим значением функции. На первом рисунке наибольшее значение функции на отрезке [a; b] достигается в точке максимума и равно максимуму функции, а на втором рисунке – наибольшее значение функции достигается в точке x = b, которая не является точкой максимума.

Билет 14 определение Максимума и минимума функции.