
- •Билет 3 Понятие предела Геометрический смысл предела
- •Билет4 Бесконечно малая и бесконечно большая
- •Бесконечно большая величина
- •Свойства бесконечно малых
- •Сравнение бесконечно малых Определения
- •Примеры сравнения
- •Понятие о непрерывности функции.
- •Максимум и минимум функции.
- •Билет 15
- •Правила дифференцирования
- •Дифференцирование сложной и обратной функций
- •2. Нахождение асимптоты
- •Тейлора формула
- •Доказательство Отношение бесконечно малых
- •Отношение бесконечно больших
- •Примеры
Бесконечно большая величина
Во
всех приведённых ниже формулах
бесконечность справа от равенства
подразумевается определённого знака
(либо «плюс», либо «минус»). То есть,
например, функция ![]() ,
неограниченная с обеих сторон, не
является бесконечно большой при
,
неограниченная с обеих сторон, не
является бесконечно большой при ![]() .
.
Последовательность
называется бесконечно
большой,
если ![]() .
.
Функция
называется бесконечно
большой в окрестности точки
,
если ![]() .
.
Функция
называется бесконечно
большой на бесконечности,
если ![]() либо
либо ![]() .
.
Свойства бесконечно малых
Сумма конечного числа бесконечно малых — бесконечно малая.
Произведение бесконечно малых — бесконечно малая.
Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
Если — бесконечно малая последовательность, сохраняющая знак, то
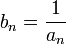 — бесконечно
большая последовательность.
— бесконечно
большая последовательность.
Сравнение бесконечно малых Определения
Допустим,
у нас есть бесконечно малые при одном
и том же ![]() величины
величины ![]() и
и ![]() (либо,
что не важно для определения, бесконечно
малые последовательности).
(либо,
что не важно для определения, бесконечно
малые последовательности).
Если
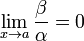 ,
то
,
то 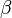 —
бесконечно малая высшего
порядка малости,
чем
—
бесконечно малая высшего
порядка малости,
чем 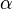 .
Обозначают
.
Обозначают 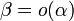 .
.Если
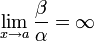 ,
то
—
бесконечно малая низшего
порядка малости,
чем
.
Соответственно
,
то
—
бесконечно малая низшего
порядка малости,
чем
.
Соответственно 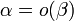 .
.Если
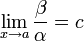 (предел
конечен и не равен 0), то
и
являются
бесконечно малыми величинами одного
порядка малости.
(предел
конечен и не равен 0), то
и
являются
бесконечно малыми величинами одного
порядка малости.
Это
обозначается как ![]() или
или ![]() (в
силу симметричности данного отношения).
(в
силу симметричности данного отношения).
Если
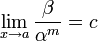 (предел
конечен и не равен 0), то бесконечно
малая величина
имеет
(предел
конечен и не равен 0), то бесконечно
малая величина
имеет 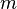 -й
порядок малости относительно
бесконечно малой
.
-й
порядок малости относительно
бесконечно малой
.
Для вычисления подобных пределов удобно использовать правило Лопиталя.
Примеры сравнения
При
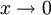 величина
величина 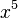 имеет
высший порядок малости относительно
имеет
высший порядок малости относительно 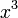 ,
так как
,
так как 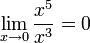 .
С другой стороны,
имеет
низший порядок малости относительно
,
так как
.
С другой стороны,
имеет
низший порядок малости относительно
,
так как 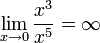 .
.
С
использованием О-символики полученные
результаты могут быть записаны в
следующем виде ![]() .
.
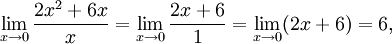 то
есть при
то
есть при 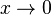 функции
функции 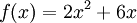 и
и 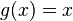 являются
бесконечно малыми величинами одного
порядка.
являются
бесконечно малыми величинами одного
порядка.
В
данном случае справедливы записи ![]() и
и ![]()
При бесконечно малая величина
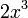 имеет
третий порядок малости относительно
имеет
третий порядок малости относительно 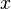 ,
поскольку
,
поскольку 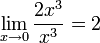 ,
бесконечно малая
,
бесконечно малая 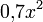 —
второй порядок, бесконечно малая
—
второй порядок, бесконечно малая 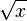 —
порядок 0,5.
—
порядок 0,5.
Билет 5 конечные пределы и их свойства
Частичные
пределы. Верхний и нижний пределы.
П. (конечный и бесконечный) какой-либо
подпоследовательности называется
частичным пределом последней. Из всякой
ограниченной последовательности можно
выделить сходящуюся подпоследовательность
(теорема Больцано — Вейерштрасса), а из
всякой неограниченной — бесконечно
большую. В множестве всех частичных П.
последовательности всегда имеется как
наибольший, так и наименьший (конечный
или бесконечный). Наибольший (соответственно
наименьший) частичный П. последовательности xn,
n = 1, 2,..., называют её верхним
(соответственно нижним) пределом и
обозначается ![]()
![]()
![]()
Последовательность имеет конечный или бесконечный П. тогда и только тогда, когда её верхний П. совпадает с нижним, при этом их общее значение и является её П. Конечный верхний П. последовательности можно также определить как такое число а, что при любом ε > 0 существует бесконечно много членов последовательности, больших, чем а — ε, и лишь не более, чем конечное число членов, больших, чем a + ε.
Предел функции. Пусть функция f, принимающая действительные значения, определена в некоторой окрестности точки x0, кроме, быть может, само́й точки x0. Функция f имеет П. в точке x0, если для любой последовательности точек xn, n = 1, 2,..., xn ≠ x0, стремящейся к точке x0,последовательность значений функции f (xn) сходится к одному и тому же числу А, которое и называется пределом функции f в точке x0, (или приx → x0) при этом пишется
![]()
или
f (x) → A при x → x0
В силу этого определения на П. функций переносятся свойства П. суммы, произведения и частного последовательностей, а также сохранение неравенств при предельном переходе.
Определение П. функции можно сформулировать и не прибегая к понятию П. последовательности: число А называется пределом функции f в точке x0, если для любого числа ε > 0 существует такое число δ > 0, что для всех точек х ≠ x0, удовлетворяющих условию ∣х — x0∣ < δ, x ≠ x0,выполняется неравенство ∣f (x) — A∣ < ε.
Все основные элементарные функции: постоянные, Степенная функция хα, Показательная функция ax, Тригонометрические функции sinx,cosx, tgx и ctgx и Обратные тригонометрические функции arcsinx, arccosx, arctgx и arcctgx во всех внутренних точках своих областей определения имеют П., совпадающие с их значениями в этих точках. Но это не всегда бывает так. Функция
![]()
являющаяся суммой бесконечной геометрической прогрессии со знаменателем q = 1/(1 + x2), 0 < q < 1, в точке х = 0 имеет П., равный 1, ибо f(x) = 1 + x2 при x ≠ 0. Этот П. не совпадает со значением функции f в нуле: f (0) = 0. Функция же
![]() x ≠
0,
x ≠
0,
вовсе не имеет П. при х → 0, ибо уже для значений xn = 1/(π/2 + πn) последовательность соответствующих значений функции f (xn) = (-1) n не имеет П.
Если П. функции при х → х0 равен нулю, то она называется бесконечно малой при х → х0. Например, функция sinx бесконечно мала при х → 0. Для того чтобы функция f имела при х → х0 П., равный А, необходимо и достаточно, чтобы f (x) = A + α(x), где α(х) является бесконечно малой при х →х0
Если
при определении П. функции f в
точке x0 рассматриваются
только точки х, лежащие
левее (правее) точки x0, то
получающийся П. называется пределом
слева (справа) и обозначается ![]()
Функция имеет П. в некоторой точке, если её П. слева в этой точке равен её П. справа. Понятие П. функции обобщается и на случай, когда аргумент стремится к бесконечности:
![]()
Например,
![]()
означает, что для любого ε > 0 существует такое δ > 0, что для всех х, удовлетворяющих условию x > δ, выполняется неравенство ∣f (x) - А∣ < ε.
Примером
функций, всегда имеющих П., являются
монотонные функции (См. Монотонная
функция). Так,
если функция f определена
на интервале (а,
b)
и не убывает, то в каждой точке х,
а < х < b, она
имеет конечный П. как слева, так и справа;
в точке в П. справа, который конечен
тогда и только тогда, когда
функция f ограничена
снизу, а в точке b П.
слева, конечный в том и только в том
случае, когда функция ограничена сверху.
В общем же случае стремление к П. может
носить разный, необязательно монотонный
характер. Например, функция f (x) = x ![]() х
→ 0 стремится к нулю, бесконечное число
раз переходя от возрастания к убыванию
и обратно.
х
→ 0 стремится к нулю, бесконечное число
раз переходя от возрастания к убыванию
и обратно.
Т. н. внутренний критерий (критерий Коши) существования П. функции в точке состоит в следующем: функция f имеет в точке x0 П. в том и только в том случае, если для любого ε > 0 существует такое δ > 0, что для всех точек х' и х ", удовлетворяющих условию ∣х’ - x0 ∣ < δ, ∣x " — x0∣ < δ, x' ≠ x0, x'’≠ x0, выполняется неравенство ∣f (x " ) — f (x')∣ < ε.
Для
функций, как и для последовательностей,
определяются понятия бесконечных П.
вида ![]() f
называется бесконечно большой
прих → х0, При х → х0 +
0 или При х → +∞ соответственно
и т.д. Например,
f
называется бесконечно большой
прих → х0, При х → х0 +
0 или При х → +∞ соответственно
и т.д. Например,
![]()
означает, что для любого ε > 0 существует такое δ > 0, что для всех х, удовлетворяющих условию х < -δ, выполняется неравенство f (x) > ε.
Билет 6 первый замечательный предел.
Первым замечательным пределом называется предел
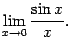
Теорема 2.14 Первый
замечательный предел равен ![]()
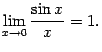
Доказательство.
Рассмотрим два односторонних
предела 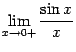 и
и 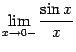 и
докажем, что каждый из них равен 1. Тогда
по теореме
2.1 двусторонний
предел
и
докажем, что каждый из них равен 1. Тогда
по теореме
2.1 двусторонний
предел 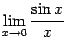 также
будет равняться 1.
также
будет равняться 1.
Итак,
пусть ![]() (этот
интервал -- одно из окончаний базы
(этот
интервал -- одно из окончаний базы ![]() ).
В тригонометрическом круге (радиуса
).
В тригонометрическом круге (радиуса ![]() )
с центром
)
с центром ![]() построим
центральный угол, равный
,
и проведём вертикальную касательную в
точке
построим
центральный угол, равный
,
и проведём вертикальную касательную в
точке ![]() пересечения
горизонтальной оси с окружностью (
пересечения
горизонтальной оси с окружностью (![]() ).
Обозначим точку пересечения луча с
углом наклона
с
окружностью буквой
).
Обозначим точку пересечения луча с
углом наклона
с
окружностью буквой ![]() ,
а с вертикальной касательной --
буквой
,
а с вертикальной касательной --
буквой ![]() ;
через
;
через ![]() обозначим
проекцию точки
на
горизонтальную ось.
обозначим
проекцию точки
на
горизонтальную ось.
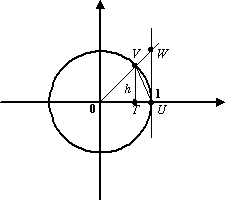
Рис.2.27.Тригонометрический круг
Пусть ![]() --
площадь треугольника
--
площадь треугольника ![]() ,
, ![]() --
площадь кругового сектора
,
а
--
площадь кругового сектора
,
а ![]() --
площадь треугольника
--
площадь треугольника ![]() .
Тогда очевидно следующее неравенство:
.
Тогда очевидно следующее неравенство:
![]()
Заметим,
что горизонтальная координата
точки
равна ![]() ,
а вертикальная --
,
а вертикальная -- ![]() (это
высота треугольника
),
так что
(это
высота треугольника
),
так что 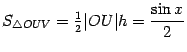 .
Площадь центрального сектора круга
радиуса
.
Площадь центрального сектора круга
радиуса ![]() с
центральным углом
равна
с
центральным углом
равна ![]() ,
так что
,
так что ![]() .
Из треугольника
находим,
что
.
Из треугольника
находим,
что ![]() .
Поэтому
.
Поэтому 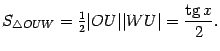 Неравенство,
связывающее площади трёх фигур, можно
теперь записать в виде
Неравенство,
связывающее площади трёх фигур, можно
теперь записать в виде
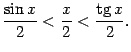
Все три части этого неравенства положительны, поэтому его можно записать так:
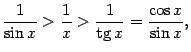
или
(умножив на ![]() )
так:
)
так:
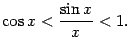
Предел
постоянной 1 в правой части неравенства,
очевидно, равен 1. Если мы покажем, что
при
предел ![]() в
левой части неравенства тоже равен 1,
то по теореме "о двух милиционерах"
предел средней части
в
левой части неравенства тоже равен 1,
то по теореме "о двух милиционерах"
предел средней части ![]() также
будет равен 1.
также
будет равен 1.
Итак,
осталось доказать, что ![]() .
Сперва заметим, что
.
Сперва заметим, что ![]() ,
так как
равняется
длине дуги окружности
,
так как
равняется
длине дуги окружности ![]() ,
которая, очевидно, длиннее хорды
,
которая, очевидно, длиннее хорды ![]() .
Применяя теорему "о двух милиционерах"
к неравенству
.
Применяя теорему "о двух милиционерах"
к неравенству
![]()
при , получаем, что
|
(2.3) |
Простая
замена переменной ![]() показывает,
что и
показывает,
что и ![]() .
Теперь заметим, что
.
Теперь заметим, что ![]() .
Применяя теоремы о линейности предела
и о пределе произведения, получаем:
.
Применяя теоремы о линейности предела
и о пределе произведения, получаем:
|
(2.4) |
Тем самым показано, что
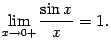
Сделаем
теперь замену ![]() ;
при этом база
перейдёт
в базу
;
при этом база
перейдёт
в базу ![]() (что
означает, что если
(что
означает, что если ![]() ,
то
,
то ![]() ).
Значит,
).
Значит,
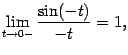
но ![]() (
(![]() --
нечётная функция), и поэтому
--
нечётная функция), и поэтому
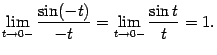
Мы показали, что левосторонний предел также равен 1, что и завершает доказательство теоремы.
Доказанная
теорема означает, что график
функции 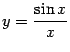 выглядит
так:
выглядит
так:
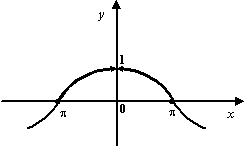
Рис.2.28.График
Билет 7. Понятие непрерывной функции
