Билет 1понятие функции способы задания функции.

Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.   Идея функциональной зависимости восходит к древности. Ее содержание обнаруживается уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами. В первых формулах для нахождения площади и объема тех или иных фигур. Так, вавилонские ученые (4-5тыс.лет назад) пусть несознательно, установили, что площадь круга является функцией от его радиуса посредством нахождения грубо приближенной формулы: S=3r². Примерами табличного задания функции могут служить астрономические таблицы вавилонян, древних греков и индийцев, а примерами словесного задания функции - теорема о постоянстве отношения площадей круга и квадрата на его диаметре или античные определения конических сечений, причем сами эти кривые выступали в качестве геометрических образов соответствующей зависимости. Раздел 1. Функция и её свойства. Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у. Переменная х- независимая переменная или аргумент. Переменная у- зависимая переменная Значение функции- значение у, соответствующее заданному значению х. Область определения функции- все значения, которые принимает независимая переменная. Область значений функции (множество значений)- все значения, которые принимает функция. Функция является четной- если для любого х из области определения функции выполняется равенство f(x)=f(-x) Функция является нечетной- если для любого х из области определения функции выполняется равенство f(-x)=-f(x) Возрастающая функция- если для любых х₁ и х₂, таких, что х₁< х₂, выполняется неравенство f(х₁)<f(х₂) Убывающая функция- если для любых х₁ и х₂, таких, что х₁< х₂, выполняется неравенство f(х₁)>f(х₂) Раздел 2. Способы задания функции. Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у=f(x), где f(x)- с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически. На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов.

Билет 2. основные элементарные функции и их графики

	Прямая линия - график линейной функции y = ax + b. Функция y монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax - прямая пропорциональность)
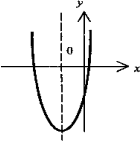
	Парабола - график функции квадратного трёхчлена у = ах2 + bх + с. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax2 + bx +с =0
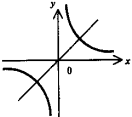
	Гипербола - график функции  . При а > О расположена в I и III четвертях, при а < 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х(а > 0) или у - - х(а < 0).
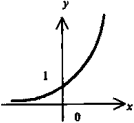
	Экспонента (показательная функция по основанию е) у = еx. (Другое написание у = ехр(х)). Асимптота - ось абсцисс.
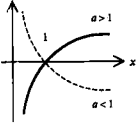
	Логарифмическая функция y = logax (a > 0)
	у = sinx. Синусоида - периодическая функция с периодом Т = 2π
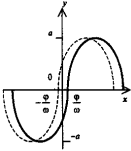
	у = а•sin(ωx+φ) - функция гармонических колебаний. Обозначения: а - амплитуда, ω - частота (ω = 2π/Т), φ - фаза (сдвиг).
	Косинусоида у = cosx (графики у = sinx и у = cosx сдвинуты по оси х на  )
	Тангенсоида y = tgx. Точки разрыва при х =  (2k -1), где k = 0, ±1, ±2,.. Вертикальные асимптоты в этих точках.
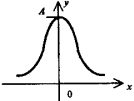
	Гауссиана у = Аe-(ax2). Кривая "нормального" закона распределения ошибок, у которого ,  , σ 2 - дисперсия ошибки. Симметрия относительно оси у.
	у = secx - кривая "цепной линии", эту форму принимает абсолютно гибкая нить, подвешенная в параллельном поле тяжести. А полная функция периодична, и её асимптоты х =  (2k -1), как у функции y = tgx.
	Круг с центром в точке (xo, yo) радиуса r. (x-xo)2 + (y-yo)2 = r2
	Эллипсс центром в точке (xo, yo). Большая полуось а, малая b, эксцинтриситет ,
	Затухающее колебание y = Ae-ax•sin(ωx+φ)

Билет 3 Понятие предела Геометрический смысл предела

В случае условия   эти множества имеют вид  ; в случае   -- вид  ; в случае   -- вид  . Назовём ихокончаниями базы предела при данном условии, а полный набор таких окончаний -- базой предела. Базу предела будем обозначать так же, как само условие, а именно,  ,  ,   и т. п. Таким образом,

Итак, база предела -- это набор окончаний, которые должны удовлетворять таким свойствам: все они непусты и если   и   -- два разных окончания (одной и той же базы), то база должна содержать третье окончание  , которое содержится в каждом из первых двух:  .

Нетрудно видеть, что в рассмотренных выше трёх примерах баз, действительно, все окончания -- непустые множества и пересечение двух окончаний совпадает с одним из них (с меньшим) и, тем самым,   можно взять равным этому меньшему окончанию. Получили, что рассмотренные наборы множеств действительно являются базами.

Произвольную базу будем обозначать  , а её окончания -- буквой  , быть может, снабжённой индексами. Если  , причём  , то окончание   будем называть более далёким, чем окончание  . Например, для базы   окончание   более далёкое, чем  , если  ; для базы   окончание   является тем более далёким, чем меньше число  .

Теперь дадим определение предела по заданной базе  .

        Определение 2.4   Пусть   -- некоторая база и функция  определена во всех точках   некоторого окончания   базы   (и, значит, определена во всех точках более далёких окончаний  ). Число  называется пределом функции   по базе   (или при базе  ) и обозначается

если

для любого (сколь угодно малого) числа   найдётся такое окончание   базы  , что при всех   выполняется неравенство

Тот факт, что  , записывают ещё в виде

    

Нетрудно заметить, что в случае баз  ,   и   это общее определение предела, при соответствующей подстановке вида окончаний этих баз, означает ровно то же самое, что приведённые выше, в предыдущем разделе, частные определения пределов.

Геометрический смысл данного определения предела таков: на плоскости  , на которой нарисован график функции  , проведём горизонтальную полосу ширины   вокруг горизонтальной прямой  . Тот факт, что  , означает, что найдётся достаточно далёкое окончание базы  , на котором график функции целиком лежит в этой полосе. При уменьшении ширины полосы окончание, возможно, придётся брать более далёким, но, всё равно, и в любую более узкую полосу умещается график на достаточно далёком окончании. 

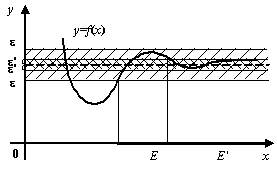
Рис.2.8.График функции, имеющей предел, умещается в любую узкую полосу на достаточно далёком Окончании

Билет4 Бесконечно малая и бесконечно большая

Бесконечно малая величина

Последовательность   называется бесконечно малой, если  . Например, последовательность чисел   — бесконечно малая.

Функция называется бесконечно малой в окрестности точки  , если  .

Функция называется бесконечно малой на бесконечности, если   либо  .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если  , то  ,  .