29.Методы построения переходных процессов

Изображение переходной функции имеет вид

.

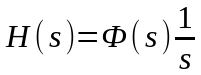Построение переходной функции при использовании таблиц преобразования Лапласа начинается с представления ее изображения в виде произведения передаточных функций типовых звеньев.

Затем это выражение преобразуется в сумму передаточных функций с неопределенными коэффициентами

(7.1.1)

В этом выражении A, B_i, C_k, D_k – неопределенные коэффициенты, _i – вещественные корни уравнения D(s)=0, а выражения s²+b_ks+c_k – соответствуют комплексно – сопряженным корням характеристического уравнения. Выражение (7.1.1) необходимо привести к общему знаменателю и числитель полученного выражения приравнять числителю изображения исходной переходной функции B(s). Приравнивая члены при одинаковых степенях оператора s в левой и правой частях, получим систему уравнений относительно неопределенных коэффициентов. Вычислив значения этих коэффициентов, обратимся к таблицам преобразования Лапласа и определим оригиналы слагаемых формулы (7.1.1). Отметим, что оригиналы, соответствующие первым двум членам суммы (7.1.1), определяются непосредственно из таблиц, определение оригиналов для третьего члена этой суммы могут потребоваться некоторые преобразования.

Оригинал переходной функции может быть получен использованием формулы обратного преобразования Лапласа, так называемой формулы разложения. В общем случае формула разложения имеет вид

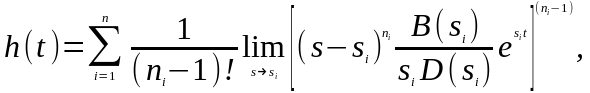(7.1.2)

где s_i – корни уравнения sD(s)=0, n_i- кратность корней. В случае только простых корней, когда среди них имются m вещественных корней и l пар комплексно – сопряженных корней, формула разложения принимает вид

(7.1.3)

В этом выражении _k и _k – вещественная и мнимая части комплексно сопряженных корней, а Амплитуда фаза колебательных составляющих определяются следующим образом:

При вычислениях по этим формулам, в первую подставляется только один из пары комплексно – сопряженных корней. При вычислении фазового сдвига необходимо учитывать квадрант, в котором находиться вектор A_ke^j_k.

30.

Коэффициенты ошибок. Числовыми показателями качества в установившемся режиме являются коэффициенты ошибок, которые определяются следующим образом. Как покажем ниже, установившуюся ошибку можно представить в виде ряда

где

Здесь — передаточная функция относительно входа g(t) и выхода e(t). Коэффициенты называются коэффициентами ошибки по задающему воздействию.

Аналогично можно представить установившуюся ошибку :

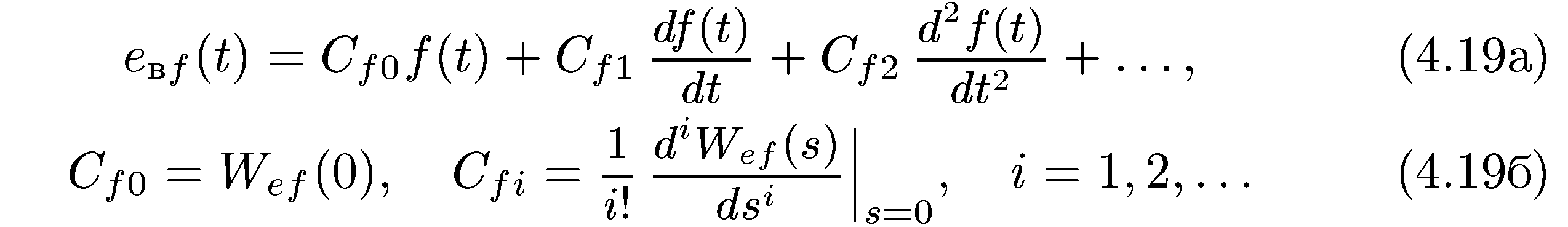
Здесь — передаточная функция относительно входа f(t) и выхода e(t). Предполагается, что возмущение не приложено в одной точке с задающим устройством. Коэффициенты называются коэффициентами ошибки по возмущению.

Первые три коэффициента ошибок имеют специальные названия:

— коэффициенты позиционной ошибки; — коэффициенты скоростной ошибки; — коэффициенты ошибки по ускорению.

31.

Показатели качества в установившемся режиме

Наиболее полной характеристикой качества системы в установившемся режиме является установившаяся ошибка. Когда внешние воздействия являются функциями времени, установившаяся ошибка как вынужденная составляющая ошибки также является функцией времени. Поэтому в общем случае установившуюся ошибку будем обозначать . Установившаяся ошибка определяется следующим образом:

Если на систему действуют два внешних воздействия — задающие воздействия g(t) и возмущения f(t), то установившуюся ошибку можно представить в виде суммы:

где — установившиеся ошибки от задающего воздействия g(t) и возмущения f(t) соответственно.