1.

Кибернетика – наука о законах управления, функционирования систем, различной сложности и разных областей на основе собераемой информации её обработки.

В технической кибернетике выделяют:

1. Теорию информационных систем, которая служит для сбора, передачи и обработки информации от различного рода ситем

2. ТАУ – занимается вопросами управления техническими системами на основе собранной информации

3. Человек и автомат

Под автоматическим управлением понимается автоматическое осуществление совокупности воздействий, выбранных из множества возможных на основании определенной информации и направленных на поддержание или улучшение функционирования управляемого объекта в соответствии с целью управления.

Управление – процесс воздействия на объект управления с целью изменения его поведения нужным образом.

Регулирование – частный случай управления, целью которого является приведение объекта к заданному состоянию.

Объект управления – техническое устройство (часть окружающего мира) или процесс, поведение которого нас не устраивает по каким-либо причинам.

В качестве объектов управления рассматриваются технические устройства и в первую очередь наиболее простые

На любой объект могут оказываться воздействия.

Воздействия – это внешние по отношению к объекту силы.

Воздействия, которые измеряются, называются контролируемыми, а иные неконтролируемые.

Иногда воздействия могут называться возмущениями.

Возмущения предполагают, что они никак не связаны с системой управления, являются внешними по отношению к ним.

2 вида возмущений:

1. Нагрузка, которая является проявлением особенностей самого объекта.

2. Помеха, которая привносится извне и которую стремятся минимизировать, с нагрузкой же приходится считаться.

Любые объекты могут изображаться в виде прямоугольников на структурных схемах:

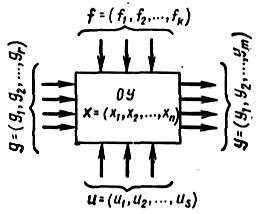
g- вектор задающих воздействий

f-вектор внешних возмущений

u-вектор управляющих воздействий

y-вектор управляемых воздействий

x-вектор состояний и параметров системы

Любой объект управления необходимо описывать математически. Все объекты управления описываются с помощью диф.уравнений.

2.

Объект управления может быть устойчивым, неустойчивым и нейтральным.

Объект устойчив, если после кратковременного внешнего воздействия он с течением времени возвратится к исходному состоянию или близкому к нему.

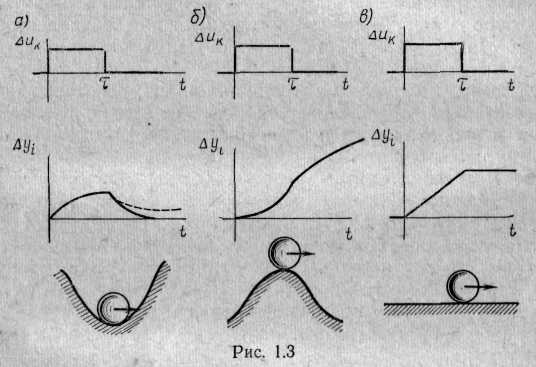
Для таких объектов может быть предложена механическая аналогия в виде шарика, находящегося в лунке, который может быть смещен при внешнем воздействии, однако возвращается обратно по окончании воздействия (рис. 1.1.5, а, внизу). Устойчивые объекты иногда называются объектами с самовыравниванием.

В неустойчивом объекте по окончании воздействия, как бы мало оно ни было, управляемая координата продолжает изменяться. Для этих объектов механическая аналогия имеет вид шарика на вершине холма (рис. 1.1. 5, б, внизу). По окончании импульса шарик продолжает удаляться от положения равновесия.

Нейтральными объектами являются такие, в которых по окончании воздействия устанавливается новое состояние равновесия, отличное от первоначального и зависящее от произведенного воздействия, Шарик на горизонтальной плоскости является механической аналогией этого типа объектов (рис. 1.1.5, в). По Ляпунову, нейтральные объекты относятся к устойчивым.

Гидравлический резервуар

Пример простейшего объекта автоматического управления показан на рис. 1.1.6, а. Управляющим воздействием и является расход воды Q, притекающей в резервуар; управляемой величиной у — уровень воды в резервуаре H, а внешним возмущением — расход воды G, вытекающей из резервуара.

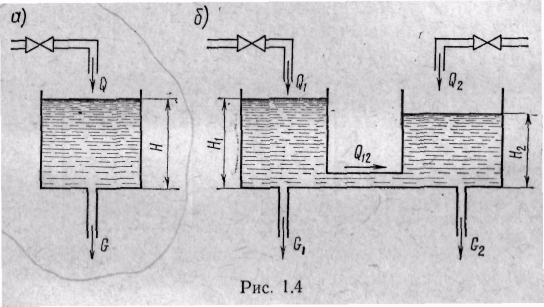
Между величинами Q, H и G может быть написана следующая зависимость:

SdH/dt = Q — G, где S — площадь поперечного сечения резервуара.

3.

Все Системы автоматического управления можно классифицировать по признакам:

1) по источнику питания:

А) Прямого действия-такие, у которых энергия для работы берется из самой системы.

Б) Непрямого действия- те, которые требуют подвода энергии

2) По типу циркулирующих сигналов:

А) Аналоговые – непрерывный во времени сигнал(синусоида)

Б) Дискретные – работает в соответствии с некоторыми импульсами(цифровые)

В) Гибридные

3) По типу диф уравнений:

А) линейные; Б) Нелинейные

4) по стационарности системы:

А) стационарные- коэффициенты диф уравнений не меняются

Б) не стационарные- коэффициенты диф уравнений могут меняться со временем

5) по характеру ошибки:

Если после прекращения кратковременного воздействия, ошибка системы стремится к нулю, то ее называют астатической.

Если же после прекращения воздействия ошибка системы стремится к значению, отличному от нуля, то она называется статической.

6) По количеству контуров управления:

А) одноконтурные(подача жидкости в сосуде, изменение объема)

Б) Многоконтурные(фрезер)

4.

Математическая модель представляет собой уравнения, передаточные или временные функции, которые описывают процессы, протекающие в системе управления. Математическая модель может быть получена аналитически (теоретически) на основе физических (химических и др.) законов, которым подчиняются процессы в системе управления, или экспериментально.

Наиболее часто в качестве математической модели объекта управления используются обыкновенные дифференциальные уравнения, которые могут быть записаны в различной форме.

Линейные многоканальные объекты обычно описывают системой дифференциальных уравнений первого порядка, представленной в векторно-матричном виде:

. (2.1.1)

Выходные переменные объекта изменяются в соответствии с уравнением выхода

(2.1.2)

Уравнения (2.1.1) и (2.1.2) описывают линейный многоканальный объект.

Для описания одноканального объекта обычно используется скалярное дифференциальное уравнение:

(2.1.3)

которое также может быть приведено к виду (2.1.1) и (2.1.2) после соответствующего выбора линейно-независимых переменных состояния.

Так как нелинейные представляют сложность при решении, то их стремятся привести к линейным. Для достижения этой цели осуществляют линеаризацию исходного диф уравнения и дальнейшее разложение в ряд Тейлора.

Пусть САУ описывается дифференциальным уравнением порядка.

при n>=m тогда система уравнений физически реализуема

Линеаризация - мы представляем ту или иную прямую в окрестности некоторой точки.

В этом выражении F и F₁ - некоторые нелинейные функции.

Разложим нелинейные функции в ряд Тейлора в окрестности установившегося режима.

Подставляем полученные выражения в исходное уравнение, при этом учтем, что порядок значений превышающих 1, произведений слагаемых, может быть приравнен к нулю.

Получим Уравнение возмущенного движения, в целях сокращения записей, знак  будем опускать. Получим

Если и оно представляет сложность, то используют преобразования Лапласа.

5.

Преобразование Лапласа предназначено для представления диф уравнения в виде алгебраического в изображениях Лапласа.

f(t) => F(s)

оригинал изображение

Прямое преобразование Лапласа:

Обратное преобразование Лапласа:

Если , то

Теорема линейности. Для любых действительных или комплексных

Теорема запаздывания. Для любого постоянного  > 0

Теорема дифференцирования оригинала. Если то

Теорема интегрирования оригинала. Если 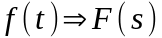и

то

Теорема о нчальном значении оригинала.

Теорема о конечном значении оригинала.

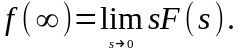
6.

На основе уравнений возмущенного движения, после преобразований Лапласа, можно получить выражение для передаточной функции:

После преобразований Лапласа получаем:

.

Обозначим:

С учетом этих обозначений исходное дифференциальное уравнение в изображениях по Лапласу получит вид

Определим теперь зависимость выходной величины от входного воздействия

Передаточная функция – называется отношение выходного сигнала к входному, выраженное в изображениях Лапласа.

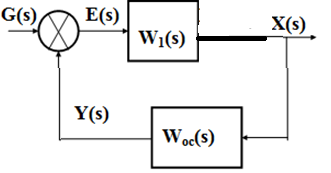
Замкнутая система

7.

Выделяют 2 временные динамические характеристики:

1. Переходная характеристика(переходная функция) h(t)- получается на выходе, когда на вход подается единичный ступенчатый сигнал

Изображение по Лапласу единичного ступенчатого воздействия будет

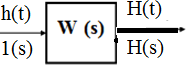
Обозначим изображение переходной функции как H(s), а передаточную функцию системы как W(s) и получим

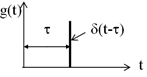
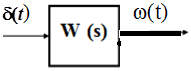
2. Импульсно переходная характеристика(весовая функция) получается на выходе, когда на вход подается дельта функция или дельта функция Дирарка. ω(t)

8.

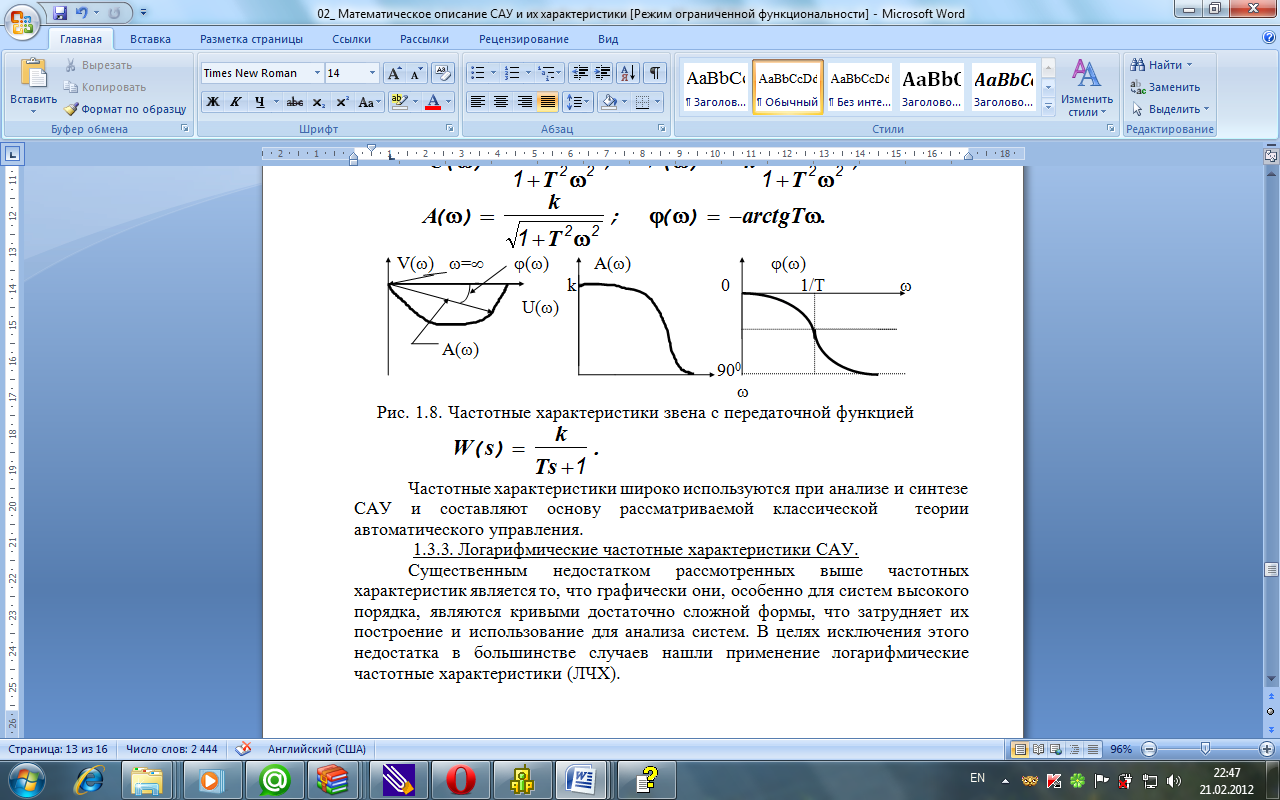
Частотные характеристики являются одними из самых удобных для анализа объекта управления, не требуя при этом достаточно сложных вычислений.

Среди основных характеристик выделяют:

1. Амплитудно-фаза частотную характеристику АФЧХ

2 формы представления частотных характеристик:

А) Нормальный вид:

Б) Если s=Ϭ±ϳω то получается расширенная частотная характеристика.

2. Амплитудно-частотная характеристика АЧХ

3. Фазо-частотная характеристика ФЧХ

9.

Логарифмические частотные характеристики:

Логарифмической амплитудной частотной характеристикой (ЛАЧХ) называется кривая, соответствующая выражению

и построенная в логарифмическом масштабе частот

Логарифмической фазовой частотной характеристикой (ЛФХ) называется фазовая частотная характеристика  (), построенная в логарифмическом масштабе частот.

Величина L() измеряется в децибелах, а ()- в градусах или радианах.

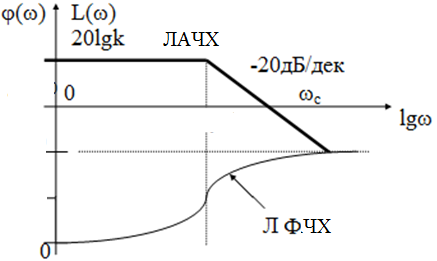
Разбиение оси абцисс в данных характеристических осуществляется по декадам и октавам.

Октава – называется изменение частоты в два раза lg2, lg4, lg8,…

Декадой называется изменение частоты в 10 раз lg10, Lg100, lg1000,…

10.

Типовым звеном называется объект, который может быть описан с помощью дифференциального уравнения или передаточной функции.

Типовым динамическим звеном называется такой объект, который описывается диф уравнением, или передаточной функцией не выше 2-го порядка.8 типовых динамических звеньев:

1. Усилительное, пропорциональное, безинерционное

Этот объект описывается передаточной функцией вида:

W(s)=K, K-коэффициент усиления

X(s)=KG(s), x(t)=Kg(t)

2. Идеально дифференцирующее звено(дифференциальное)

W(s)=KS

3. Идеально интегрирующее звено(интегральное)

W(s)=K/S

4. Инерционное звено 1-го порядка(апериодическое звено 1 порядка)

W(s)=K/(ТS+1), Т-постоянная времени(сек,мин,…)

5. Звено 2-го порядка

W(s)=K/(Т^2*S^2+2*ξ*T*S+1),где ξ-коэффициент

ξϵ[0;1] то звено колебательное

ξ>1- апериодическое звено

ξ=0 – консервативный объект

6. Звено форсирующее 1 порядка

K(ТS+1),

7. Звено форсирующее 2 порядка

W(s)=K(Т^2*S^2+2*ξ*T*S+1)

8. Звено запаздывания

W(s)=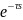 где - время запаздывания(пока на выходе держится ноль)

11.

Существует 3 основных типа соединения звеньев:

1. Последовательное соединение звеньев

При последовательном соединении выходной сигнал предыдущего объекта является входным для последующего.

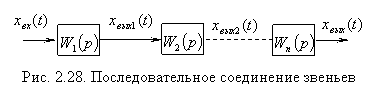
W_n(p)=

x_вых x_вх(p).

2. Параллельное соединение

При параллельном соединении на вход всех звеньев поступает одинаковый входной сигнал, а выходной сигнал получается как сумма выходных всех этих звеньев.

- сумматор, устройство, которое суммирует входные сигналы.

В закрашенные сектора «-» в прозрачные «+».

W(p) =

x_вых(p)=

3. Встречно-параллельное соединение

x(t)-ошибка системы

E(p)=G(p)-Y(p)

Y(p)= W₂(p)*X(p)

X(p)=W₁(p)* E(p)

W_З(p) = -передаточная функция замкнутой системы

передаточная функция замкнутой системы

- передаточная функция разомкнутой системы

- ошибка

W_E(p) = 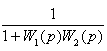 -передаточная функция ошибки

12.

1) Усилительное, пропорциональное, безинерционное

Этот объект описывается передаточной функцией вида:

W(s)=K, K-коэффициент усиления

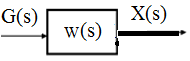X(s)=KG(s), x(t)=Kg(t)

ФЧХ звена: ;

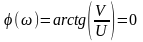АЧХ: ;

ЛАХ звена: .

Переходная характеристика .

Весовая функция .

2) Идеально дифференцирующее звено(дифференциальное)

W(s)=KS

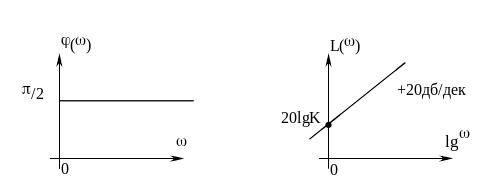
3) Идеально интегрирующее звено(интегральное)

W(s)=K/S

13.

1. Инерционное звено 1-го порядка(апериодическое звено 1 порядка)

W(s)= Т-постоянная времени(сек,мин,…)

X(s)= G(s),

передаточная функция

АФЧХ -

АЧХ

ФЧХ: ,

2) Звено 2-го порядка

W(s)=K/(Т^2*S^2+2*ξ*T*S+1),где ξ-коэффициент

ξϵ[0;1] то звено колебательное

ξ>1- апериодическое звено

ξ=0 – консервативный объект

14.

1. Звено форсирующее 1 порядка

W(s)= K(ТS+1),

2. Звено форсирующее 2 порядка

W(s)=K(Т^2*S^2+2*ξ*T*S+1)

3. Звено запаздывания

W(s)= где - время запаздывания(пока на выходе держится ноль)

; ; ; .

Переходная характеристика

ℒ^-1 ℒ^-1 .

Весовая функция .

15.

Математическую модель САУ можно наглядно представить с помощью ориентированных графов. Орграфом САУ является графическое представление САУ в виде совокупности вершин, соответствующих переменным, и дуг, соединяющих вершины.

Основные свойства орграфа:

Каждая дуга со стрелкой, указывающей направление распространения сигнала, изображает звено и характеризуется оператором изображаемого звена (передаточной функцией);

Каждой вершине, отмеченной кружком, ставится в соответствие одна из переменных САУ (изображение переменной по Лапласу);

Входная величина дуги равна переменной вершины, из которой эта дуга исходит;

Выходная величина дуги получается как результат преобразования оператором входной величины;

Если к вершине подходят несколько дуг, то соответствующая вершине переменная равна сумме выходных величин этих дуг (аналог суммирующего звена структурных схем);

Если из вершины исходит несколько дуг, то входные величины всех этих дуг одинаковы (аналог точки ветвления в структурных схемах).

Ориентированный граф (орграф) можно построить по структурной схеме и наоборот. При построении орграфа по структурной схеме необходимо придерживаться следующих правил:

Модифицируют структурную схему так, чтобы в сумматорах все переменные складывались с положительным знаком, отрицательные знаки вносятся в передаточные функции соответствующих звеньев;

Каждый сумматор структурной схемы заменяется вершиной, которой ставится в соответствие выходная переменная сумматора;

Каждое динамическое звено заменяется дугой с оператором, равным передаточной функции звена;Каждой переменной, включая и входные воздействия, соответствует своя вершина.

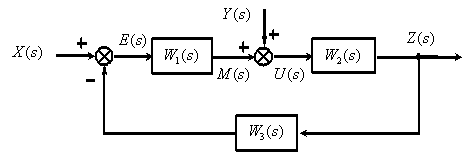
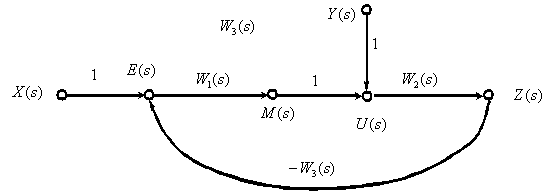
Последовательное соединение динамических звеньев.

Параллельное соединение динамических звеньев.

Замкнутый контур с отрицательной обратной связью.

16.

формулу Мейсона где - передаточная функция -го отдельного прямого пути от до , вычисленная как произведение передаточных функций дуг, входящих в этот путь;

- определитель орграфа.

(3.3.12)

где - передаточная функция -го замкнутого контура, вычисленная как произведение передаточных функций дуг, входящих в этот контур;

- произведение передаточных функций пары ( -го и -го) замкнутых контуров, не касающихся ни дугами, ни вершинами, суммирование осуществляется по всем парам некасающихся контуров;

- произведение тройки ( -го, -го и -го) некасающихся контуров, суммирование производится по всем тройкам не касающихся контуров.

    - определитель орграфа, полученного при удалении дуг и вершин -го отдельного прямого пути, определяется по формуле (3.3.12).

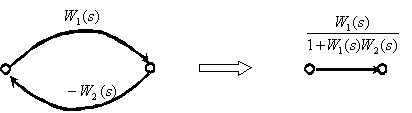
16. Преобразование графа системы управления. Формула Мейсона. Параллельные дуги, т.е. дуги, имеющие общие начальные и конечные вершины, можно заменить одной дугой с передаточной функцией, равной сумме передаточных функций исходных дуг (рис. 2.25, а).

Простой путь, если нет не принадлежащих ему дуг, входящих или выходящих из промежуточных вершин этого пути, можно заменить одной дугой с передаточной функцией, равной произведению передаточных функций дуг этого пути (рис. 2.25, б).

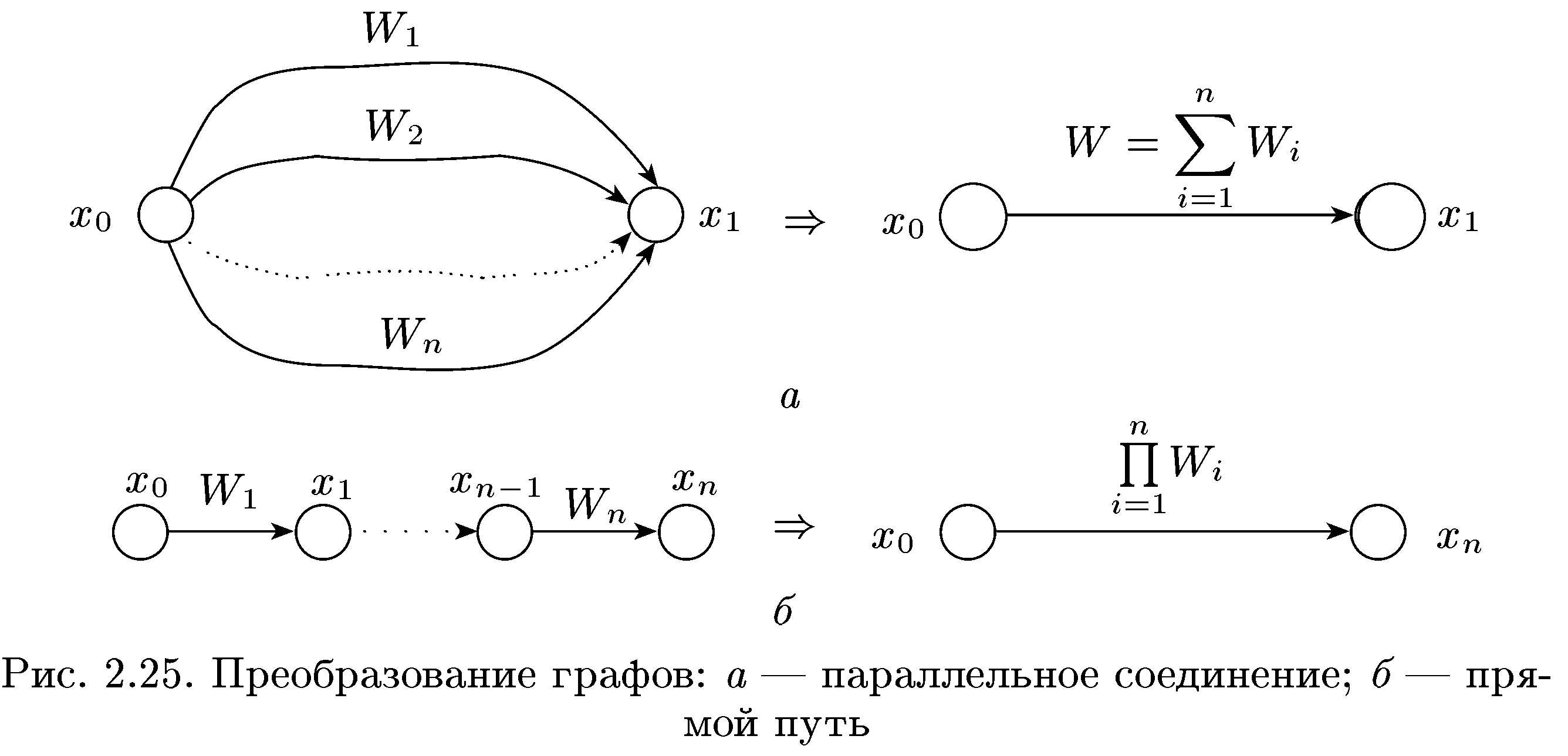
Для преобразования графа и вычисления передаточной функции системы управления по ее графу можно воспользоваться теоремой (формулой) Мейсона.

Определителем графа называется передаточная функция , которая определяется следующим образом:

Здесь в первой сумме W_0j — передаточная функция j-ro простого контура, равная произведению передаточных функций дуг, входящих в этот контур, и суммирование производится по всем простым контурам; во второй сумме W_ojW_0k произведение передаточных функций j-гo и к-k-го простых контуров и суммирование производится по всем несоприкасающимся парам контуров; в третьей сумме W_0jW_0kW_0l — произведение передаточных функций j-гo, k-го и 1-го простых контуров, и суммирование производится по всем несоприкасающимся тройкам контуров и т.д.

Формула Мейсона. Передаточная функция системы управления относительно каких-либо входа х и выхода z определяется следующим образом:

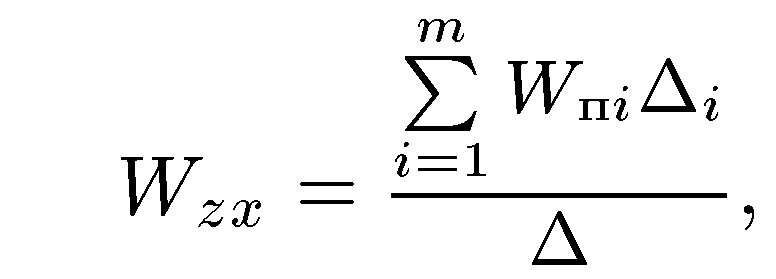
где — определитель графа системы управления; W_пi — передаточная функция i-го прямого пути от начальной вершины x к конечной вершине z; m — общее число таких прямых путей; — определитель подграфа i-го прямого пути.

17. Основное условие устойчивости.

Корневой критерий устойчивости Для того чтобы система управления была устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения имели отрицательную вещественную часть. На комплексной плоскости корни, имеющие отрицательную вещественную часть, располагаются в левой полуплоскости-называются левыми] корни, с «+» вещественную часть, располагаются в правой полуплоскости -правые] а корни, на мнимой оси, называются нейтральными.

Теоремы Ляпунова об устойчивости по линейному приближению.

Практически все системы управления являются нелинейными, а линейные системы управления следует рассматривать как приближенные, линеаризованные модели нелинейных систем.

Линеаризация производится относительно заданного номинального режима y°(t), называемого в теории устойчивости невозмущенным движением. Невозмущенное движение y°(t) нелинейной системы называется асимптотически устойчивым, если существует некоторая окрестность вокруг невозмущенного движения такая, что любое возмущенное движение y(t), начинающееся в момент t_о окончания действия возмущения в этой окрестности, в дальнейшем не выходит из этой окрестности и при

Теоремы Ляпунова.

1. Если все корни характеристического уравнения линеаризованной модели являются левыми, то невозмущенное движение соответствующей нелинейной системы асимптотически устойчиво.

2.Если среди корней характеристического уравнения линеаризованной модели имеется правый корень, то невозмущенное движение соответствующей нелинейной системы неустойчиво.

3.Случай, когда среди корней характеристического уравнения линеаризованной модели имеются нейтральные корни (корни на мнимой оси), но нет правых корней, называют критическим. В критическом случае по линеаризованной модели нельзя судить об устойчивости невозмущенного движения нелинейной системы.

18. Алгебраическими критериями устойчивости называются такие условия, составленные из коэффициентов характеристического уравнения, при выполнении которых система устойчива, а при невыполнении — неустойчива.

Необходимое условие устойчивости. Для того чтобы система была устойчива, необходимо, чтобы все коэффициенты ее характеристического уравнения были положительны.

Критерий Гурвица. Из коэффициентов характеристического полинома

составляется определитель n-го порядка

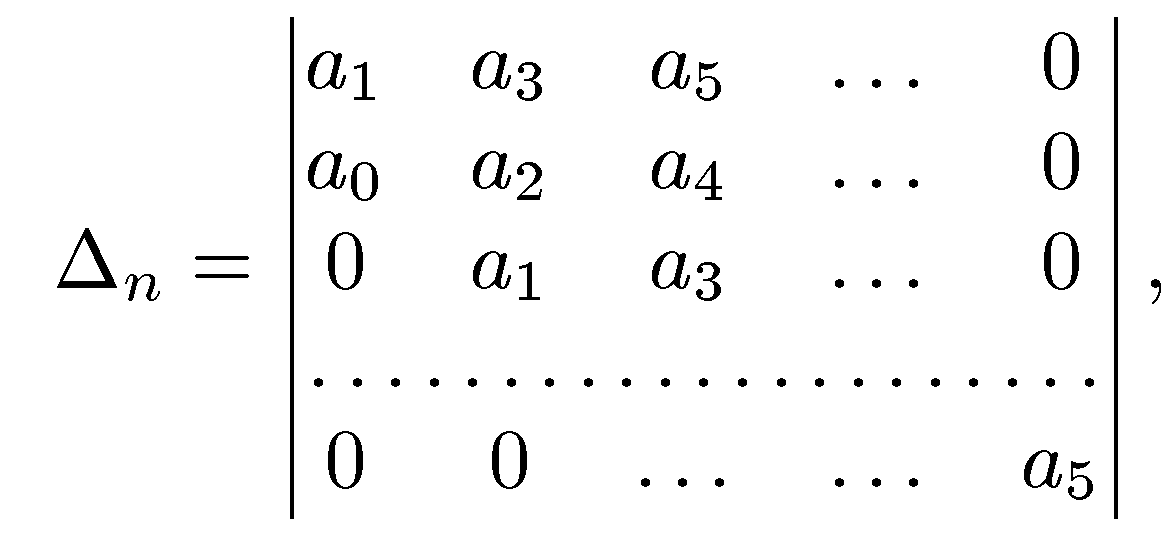
Главные миноры определителя

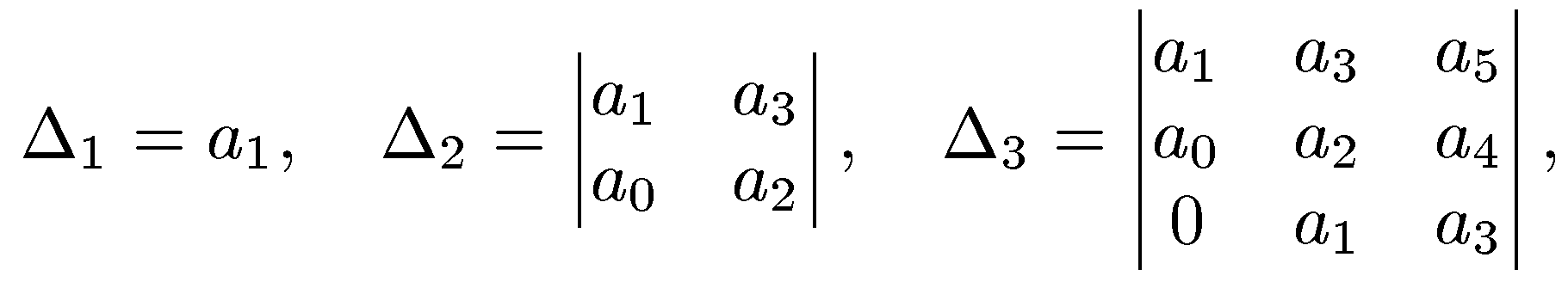
включая сам определитель , называют определителями Гурвица.

Критерий Гурвица). Для того чтобы система была устойчива, необходимо и достаточно, чтобы определители Гурвица, составленные из коэффициентов ее характеристического уравнения, при были больше нуля:

Критерий устойчивости Рауса

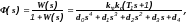
Таблица Рауса

i (номер строки	k (номер столбца)
	1	2	3	4
1	d0	d2	d4	…
2	d1	d3	d5	…
3	c13	c23	c33	…
4	c14	c24	c34	…
5	c15	c25	…	…

Элементы каждой строки для i>2 вычисляются по формуле

Для того, чтобы корни характеристического уравнения лежали в левой полуплоскости и система была устойчива, необходимо и достаточно, чтобы все элементы первого столбца таблицы Рауса были строго положительны.

19. Частотными критериями устойчивости называются условия устойчивости, основанные на построении частотных характеристик и так называемой кривой Михайлова. Выражение

которое получается при подстановке в характеристический полином, называется характеристическим вектором; переменная и называется частотой. Частотные критерии получаются из принципа аргумента. Поэтому сначала рассмотрим этот принцип.

Принцип аргумента.

Изменение аргумента вектора D(j) при изменении частоты от - до + равно разности между числом (n-m) корней уравнения D(s)=0, лежащих в левой полуплоскости, и числом m корней этого уравнения, лежащих в правой полуплоскости, умноженной на  .

20. Критерий устойчивости Михайлова.

1 Критерий Михайлова: Система автоматического управления устойчива, если при возрастании частоты от - до + изменение аргумента вектора D(j) будет равно n, где n- порядок характеристического уравнения.

Система автоматического управления устойчива, если при возрастании частоты от 0 до + вектор D(j) повернется на угол n/2 или, что то же самое, если кривая Михайлова при том же изменении частоты, начиная с положительной вещественной полуоси, обходит последовательно в положительном направлении n квадрантов и заканчивается в n-ом квадранте.

Если хотя бы один квадрант пропущен (рис.6.2.3), то система неустойчива.

2 критерий Михайлова: Система автоматического управления устойчива, если корни уравнений V()=0 и U()=0 вещественные и чередуются между собой.

21. Критерий Найквиста.

Критерий устойчивости Найквиста позволяет судить об устойчивости замкнутой системы по виду АФЧХ разомкнутой системы.

Система автоматического управления, устойчивая в разомкнутом состоянии, будет устойчивой и в замкнутом состоянии, если АФЧХ W(j) разомкнутой системы при изменении частоты от 0 до  не охзватывает критическую точку с координатами (-1, j0).

Система, неустойчивая в разомкнутом состоянии, будет устойчивой в замкнутом состоянии, если АФЧХ W(j с) разомкнутой системы при изменении частоты от 0 до  охватывает критическую точку (-1,j0) в положительном направлении ровно р/2 раз, где р- число правых полюсов разомкнутой системы.

Система, неустойчивая в разомкнутом состоянии, будет устойчивой в замкнутом состоянии, если разность между числом положительных и отрицательных переходов АФЧХ разомкнутой системы равна р/2.

Запасы устойчивости

Угол , образуемый прямой, проходящей через точку пересечения АФЧХ с окружностью единичного радиуса, что соответствует частоте среза системы, и отрицательной вещественной полуосью называется запасом устойчивости системы по фазе.

(6.2.11)

Запасом устойчивости по модулю называется величина

(6.2.12)

где А(_)- значение АФЧХ при частоте =_ , при которой она пересекает вещественную ось.