
- •Механика и её разделы.
- •2. Кинематика произвольного движения. Связь между угловыми и линейными величинами.
- •3. Динамика материальной точки и поступательного движения. Законы Ньютона. Масса. Сила.
- •4. Импульс материальной точки и тела. Закон сохранения импульса. Центр масс системы тел и закон его движения.
- •5. Сила инерции. Центробежная сила.
- •23.Поток вектора электрического поля. Теорема Гаусса.
- •24) Условия существования постоянного электрического тока.
- •27) Классическая теория
- •31) Сила Лоренца
4. Импульс материальной точки и тела. Закон сохранения импульса. Центр масс системы тел и закон его движения.
Импульсом материальной
точки называют величину равную
произведению массы точки на ее скорость:
![]()
Закон сохранения импульса :
Векторная сумма импульсов двух тел до взаимодействия равна векторной сумме их импульсов после взаимодействия.
Центр масс — это геометрическая точка, характеризующая движение тела или системы частиц как целого.
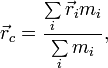
![]() — радиус-вектор центра
масс,
— радиус-вектор центра
масс,
![]() —
радиус-вектор i-й
точки системы,
—
радиус-вектор i-й
точки системы,
![]() — масса i-й
точки.
— масса i-й
точки.
Короче у нас имеется сложное тело, состоящее из простых, мы умножаем массу тела на расстояние до точки вращения и радуемся.
5. Сила инерции. Центробежная сила.
Сила инерции – это сила, которая возникает в системе отсчета (СОД), движущейся относительно лабораторной системы отсчета (ЛСО).
Сила
инерции определяется по формуле где m –
масса тела,
По определению, центробежной силой называется сила инерции (то есть в общем случае — часть полной силы инерции) в неинерциальной системе отсчета, не зависящая от скорости движения материальной точки в этой системе отсчета, а также не зависящая от ускорений (линейных или угловых) самой этой системы отсчета относительно инерциальной системы отсчета. Для материальной точки центробежная сила выражается формулой:
где:
Эквивалентное выражение для центробежной силы можно записать как
если
использовать обозначение Центробежная сила для тел конечных размеров может быть рассчитана (как это обычно делается и для любых других сил) суммированием центробежных сил, действующих на материальные точки, являющиеся элементами, на которые мы мысленно разбиваем конечное тело. 6.Энергия и работа. Мощность. Кинетическая энергия. Консервативные и неконсервативные силы. Закон сохранения энергии. Работа и Энергия Термин "работа" в механике имеет два смысла: работа как процесс, при котором сила перемещает тело, действуя под углом, отличном от 90°; работа - физическая величина, равная произведению силы, перемещения и косинуса угла между направлением действия силы и перемещением: А = Fs cos a. Работа равна нулю, когда тело движется по инерции (F = 0), когда нет перемещения (s = 0) или когда угол между перемещением и силой равен 90° (cos а = 0). Единицей работы в СИ служит джоуль (Дж). 1 джоуль - это такая работа, которая совершается силой 1 Н при перемещении тела на 1 м по линии действия силы. Для определения быстроты совершения работы вводят величину "мощность". Мощность равняется отношению совершенной работы ко времени, за которое она выполнена:
Единицей мощности в СИ служит 1 ватт (Вт). 1 Вт - мощность, при которой совершается работа в 1 Дж за 1 секунду. Кинетическая энергия - энергия движения, ею обладают все движущиеся тела. Эта величина является относительной, то есть она изменяется в зависимости от выбранной системы отсчета. Кроме этого вида механической энергии, существует и другой ее вид - потенциальная энергия. Рассмотрим систему двух взаимодействующих тел. Например, тела, поднятого над Землей, и саму Землю. Работа силы тяжести при перемещении тела на отрезке |h1 - h2| будет равна:
Величину mgh в соответствующей точке, которая расположена на высоте h, называют потенциальной энергией тела, находящегося в поле тяжести. Из предыдущего уравнения вытекает, что работа не зависит от траектории движения в доле силы тяжести, а определяется лишь изменением высоты. Потенциальная энергия характеризует и другие взаимодействующие тела. Так, потенциальной энергией обладает сжатая пружина:
где k - модуль упругости, х - смещение от положения равновесия. Потенциальная энергия, как и кинетическая, является величиной относительной, поскольку и высота, и смещение зависят от выбора точки отсчета.
консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил)[1]. Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0. Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется. Для консервативных сил выполняются следующие тождества:
Силы, что не принадлежат к консервативным, называют неконсервативными: - силы трения, которые возникают при скольжении одного тела по поверхности другого - силы сопротивления, которых испытывает тело, двигаясь в жидкой или газообразной среде Следовательно, к консервативным силам относят силы притяжения, силы упругости и силы электростатического взаимодействия; к неконсервативным соответственно - силы трения и силы сопротивления. Этот закон гласит, что энергия не может исчезать бесследно или возникать из ничего. Полная энергия замкнутой системы, которая не отдает своей энергии и не получает энергии извне, остается неизменной. Этот общий закон в применении к механике означает следующее: Закон сохранения механической энергии В замкнутой механической системе сумма механических видов энергии (потенциальной и кинетической энергии, включая энергию вращательного движения) остается неизменной.
Здесь: Wп — Потенциальная энергия тела, энергия положения (Джоуль), Wк — Кинетическая энергия тела, энергия движения (Джоуль), Wвр — Энергия вращения тела (Джоуль),
Сила приложенная к твердому телу, которое может вращаться вокруг некоторой точки, создает момент силы. Действие момента силы аналогично действию пары сил.
Момент силы относительно некоторой точки — это векторное произведение силы на кратчайшее расстояние от этой точки до линии действия силы. Единица СИ момента силы:
Если: M — момент силы (Ньютон · метр), F — Приложенная сила (Ньютон), r — расстояние от центра вращения до места приложения силы (метр), l — длина перпендикуляра, опущенного из центра вращения на линию действия силы (метр), α — угол, между вектором силы F и вектором положения r, То
или в виде векторного произведения
М
Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
Закон сохранения момента импульса.
Если
система замкнута, т.е. внешних сил
нет (
8.Закон всемирного тяготения. Гироскопы. Исаак Ньютон смог объяснить движение тел в космическом пространстве с помощью закона всемирного тяготения. Ньютон пришел к своей теории в результате многолетних исследований движения Луны и планет.
где G = 6,67∙10–11 Н∙м2/кг2 – гравитационная постоянная. Этот закон справедлив также для сферически симметричных тел (при расстояниях между центрами больше суммы их радиусов), а приближенно он выполняется для любых тел, если расстояние между ними велико по сравнению с их размерами.
Ускорение,
которое испытывает тело m,
находящееся на расстоянии r от
тела M,
равно Гироско́п — устройство, способное реагировать на изменение углов ориентации тела, на котором оно установлено, относительно инерциальной системы отсчета. Простейший пример гироскопа — юла (волчок).
ро́торный гироско́п — быстро вращающееся твёрдое тело (ротор), ось вращения которого может свободно изменять ориентацию в пространстве. При этом скорость вращения гироскопа значительно превышает скорость поворота оси его вращения Вибрационные гироскопы — устройства, сохраняющие плоскость своих колебаний при повороте основания Оптические гироскопы Схема лазерного гироскопа. Здесь луч лазера циркулирует с помощью зеркал и постоянно усиливается лазером. Замкнутый контур имеет ответвление в датчик на базе интерферометра. Делятся на волоконно-оптические и лазерные гироскопы. Принцип действия основан на эффекте Саньяка, открытом в 1913 году[12][13]. Теоретически он объясняется с помощью СТО. Согласно СТО скорость света постоянна в любой инерциальной системе отсчёта[14]. В то время как в неинерциальной системе она может отличаться от c[15]. При посылке луча света в направлении вращения прибора и против направления вращения разница во времени прихода лучей (определяемая интерферометром) позволяет найти разницу оптических путей лучей в инерциальной системе отсчёта, и, следовательно, величину углового поворота прибора за время прохождения луча. Величина эффекта прямо пропорциональна угловой скорости вращения интерферометра и площади, охватываемой путём распространения световых волн в интерферометре.
ВРАЩЕНИЕ ВОКРУГ НЕПОДВИЖНОЙ ОСИ Вращением вокруг неподвижной оси называется такое движение твердого тела, при котором во все время движения две его точки остаются неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, по окружностям, центры которых лежат на оси вращения. Положение вращающегося твердого тела определяется одним параметром - углом φ между начальным положением АМ0О некоторой плоскости, связанной с телом и проходящей через ось, и ее положением АМО в данный момент времени (рис. 1). Рисунок 1. Закон вращательного движения:
Проекция вектора угловой скорости на ось и определяется зависимостью:
Угловая скорость ω рад/сек связана с числом оборотов в минуту n зависимостями:
Проекция вектора угловой скорости на ось u определяется зависимостью
Скорость и ускорение точки М вращающегося твердого тела определяются соотношениями (рис. 1):
или в скалярной форме:
Частные случаи: 1) равномерное вращение (ε=0):
2) равнопеременное вращение (εu=const):
Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Единица измерения СИ: кг·м². Обозначение: I или J. Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
где:
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
где:
Если тело однородно, то есть его плотность всюду одинакова, то
[править]Теорема Гюйгенса-Штейнера Основная статья: Теорема Штейнера Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласнотеореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
где — полная масса тела. Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
10.Основное уравнение динамики вращательного движения твердого тела. Примеры вычислений момента инерции различных тел.
Рассмотрим
материальную точку массой
Рисунок 3.2 Материальная точка, движущаяся по окружности под действием силы, направленной по касательной к окружности.
Тогда,
по второму закону Ньютона, Эта сила
вызывает тангенциальное ускорение
Умножим
обе части полученного равенства на
Левая
часть последнего уравнения является
моментом силы:
Таким образом мы получили основное уравнение динамики вращательного движения материальной точки: угловое ускорение материальной точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции. Примеры вычисления моментов инерции. Найдем связь между моментами инерции тела относительно двух различных параллельных осей О и А. Радиус-вектор точки r и r’ соответственно, а=ОА (вектор),r’=r-a, r’2=r2+a2-2(ar). sum r’2 dm = sum r2dm + a2 sum dm – 2(a sum r dm). sum r dm =mR_c, где R_c – радиус-вектор центра масс относительно О. I_A=I_O+ma2-2m(aRc). Если ось О проходит через центр масс тел, то I_a=I_c+ma2 – теорема Гюйгенса-Штейнера: момент инерции тела относительно какой-либо оси равен моменту инерции его относительно параллельной оси, проходящей через центр масс, сложенному с величиной ma2, где а – расстояние между осями. I=sum r2 dm. В общем случае I=kml2, l – характерный размер, k зависит от формы тела. 1. Момент инерции тонкого однородного стержня относительно перпендикулярной оси. А – ось, проходящая через конец стержня, С – через центр. I_a=kml2,I_a=I_c+m(l/2)2. С другой стороны, как сумма моментов двух стержней I_c=km(l/2)2.kml2=km(l/2)2+m(l/2)2. I_a=ml2/3, I_c=ml2/12. 2. Момент инерции однородных прямоугольных пластинки и параллелепипеда. Пусть оси X и Y проходят через центр пластинки и параллельны её сторонам, a и b – длина пластинки по X и Y. Сместим вещество пластинки на ось Y параллельно оси X. Расстояния относительно оси X не изменятся, пластинка перейдет в тонкий стержень, I_x=mb2/12, I_y=ma2/12. I_z=m/12 (a2+b2). 3. Бесконечно тонкое круглое кольцо. I_z=mR2. I_x=I_y=mR2/2 (плоское распределение 17.Первое начало термодинамики. Теплоемкость. 1. Первый закон термодинамики, установленный на основании многочисленных опытов, утверждает, что изменение внутренней энергии ΔU системы равно сумме совершаемой над системой работы A' внешних сил и количества теплоты Q, переданного системе извне.
Этот закон можно сформулировать несколько иначе, если вместо работы A' внешних сил говорить о работе A самой системы. Поскольку A' = – A, то
таким образом, полученное системой количество теплоты равно сумме изменения ее внутренней энергии и работы, совершаемой системой над внешними телами. 2. Рассмотрим систему, которая получает энергию в процессе теплообмена. Пусть для изменения температуры системы на ΔT потребовалось количество теплоты Q. Теплоемкостью системы называется величина
Если в качестве системы рассматривать 1 моль вещества, то теплоемкость, определяемая соотношением (4.20), называется молярной теплоемкостью. Удельная теплоемкость (теплоемкость единицы массы вещества) связана с молярной теплоемкостью очевидным равенством:
При
изохорном процессе
Для изобарного процесса, используя равенства (4.16), (4.19) и (4.22), получаем
Уравнение (4.23) показывает, что теплоемкость СР больше СV на величину работы, совершаемой системой при ее изобарном нагревании на 1ºС. Для моля идеального газа уравнение состояния имеет вид:
Применение этого уравнения к двум состояниям моля газа в изобарном процессе приводит к соотношению
18.Применение второго начала термодинамики. Цикл Карно. Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами. Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения. Существуют несколько эквивалентных формулировок второго начала термодинамики:
Для получения математического выражения второго начала термодинамики рассмотрим работу идеальной тепловой машины (машины, обратимо работающей без трения и потерь тепла; рабочее тело – идеальный газ). Работа машины основана на принципе обратимого циклического процесса – термодинамического цикла Карно (рис. 1.2).
Рисунок 1.2 Цикл Карно Запишем выражения для работы на всех участках цикла: Участок 1 – 2: Изотермическое расширение.
Участок 2 – 3: Адиабатическое расширение.
Участок 3 – 4: Изотермическое сжатие.
Участок 4 – 1: Адиабатическое сжатие.
Общая работа в цикле равна сумме работ на всех участках:
Проведя ряд несложных преобразований, получим для КПД идеальной тепловой машины, работающей по циклу Карно:
19.Гармонические колебания. Уравнение гармонических колебаний. Важное место среди разнообразных форм колебаний занимают гармонические колебания. Гармонические колебания - это простейшие периодические колебания. Большинство колебаний, встречающихся на практике, являются сложными. Из курса математики извесно (теорема Фурье), что любое сложное периодическое колебание представляет собой сумму простейших гармонических колебаний (гармоник). Уравнение гармонических колебаний Ниже представлено уравнение гармонических колебаний. Это уравнение дает зависимость колеблющейся величины S от времени t
так как синус изменяется в пределах от +1 до -1, то амплитуда (А) может принимать значение от +А до -А.
20.Упругие волны. Механизм волнового движения. Упру́гие во́лны (звуковые волны) — волны, распространяющиеся в жидких, твёрдых и газообразных средах за счёт действия упругих сил. Упругие волны в твёрдых телах Наиболее распространёнными типами упругих волн в твёрдых телах являются: продольные волны — волны с колебанием частиц вдоль направления распространения волны; поперечные волны — волны с колебанием частиц перпендикулярно направлению распространения волны; поверхностные волны (например волны Рэлея — волны с колебанием частиц по эллипсам вдоль поверхности тела; волны Лэмба — волны в тонких пластинах; изгибные волны — распространение колебаний деформации изгиба в стержнях или пластинах, длина волны которых много больше толщины стержня или пластины
В
жидкостях и газах, к-рые обладают
упругостью объёма, но не обладают
упругостью формы, могут распространяться
лишьпродольные
волны разрежения-сжатия,
где колебания частиц среды происходят
в направлении распространения волны.
Фазовая скорость их
НОВЫЕ СИЛЫ И ВОЛНОВЫЕ МЕХАНИЗМЫ ДВИЖЕНИЯ В ГИДРОМЕХАНИЧЕСКИХ СИСТЕМАХ ВОЛНОВЫЕ СИЛЫ И ВОЛНОВЫЕ МЕХАНИЗМЫ ДВИЖЕНИЯ В ГИДРОМЕХАНИЧЕСКИХ СИСТЕМАХ 6 1. Создание мощных направленных потоков (также кавитационные процессы), которые пробивают стальные изделия толщиной 5-10 см. 2. Создание управляемых процессов турбулизации и ламинаризации потоков, повышающих бесшумность и производительность. 3. Интенсивное смешение, тонкое диспергирование (1 мкм до нм) и активация жидкостей (вязких и высоковязких). 4. Измельчение, диспергирование, активация порошков и сухих смесей с целью получения уникальных материалов, выделение ценных компонентов из руды. 5. Фильтрация и пропитка пористых сред (многократная их интенсификация 10 – 1000 раз). 6. Волновые силы в сжимаемой жидкости в 10 -10 2 раз превышают силы радиационного давления, позволяют уменьшать вязкость от 2 до 13 раз. Эти процессы не могут быть в принципе получены другими, известными в настоящее время, методами. Они являются научным базисом для создания новых машин и волновых технологий
21. Электрическое поле в вакууме. Закон Кулона.
1. Сила взаимодействия двух неподвижных
точечных зарядов
где
2. Напряженность электрического поля
где q – положительный точечный
заряд, помещенный в данную точку поля,
Напряженность поля точечного заряда q:
3. Теорема Остроградского-Гаусса для
вектора
В дифференциальной форме:
( 4. Циркуляция вектора напряженности электростатического поля по произвольному замкнутому контуру:
5. Разность потенциалов
6. Электрический дипольный момент
7. Энергия взаимодействия двух точечных зарядов, находящихся в вакууме на расстоянии друг от друга:
где
Полная электрическая энергия системы с непрерывным распределением заряда:
где
8. Плотность энергии электрического поля в вакууме
. Закон Кулона - это закон взаимодействия двух неподвижных точечных зарядов. Закон Кулона формулируется следующим образом: Сила электрического взаимодействия между двумя точечными зарядами в вакууме пропорциональна этим зарядам и обратно пропорциональна квадрату расстояния между ними. При взаимодействии одноименные заряды отталкиваются, разноименные притягиваются. Силы Кулона направлены по прямой, соединяющей заряды. Закон Кулона для взаимодействия точечных зарядов Q1 и Q2, находящихся на расстоянии r друг от друга, записывается формулой:
Сила отталкивания F, действующая на заряд Q2 со стороны одноименного заряда Q1, совпадает по направлению с радиусом-вектором r, проведенным из Q1 к этому заряду.
22. Работа в электрическом поле. Потенциал
Работа
сил в однородном электрическом
поле. Докажем
независимость работы сил электростатического
поля от вида траектории движения
заряда между двумя точками однородного
поля. Пусть в однородном электрическом
поле напряженностью
где
S – модуль вектора перемещения,
Если
заряд из точки B сначала
движется по прямой в точку C,
а затем по прямой из точки C в
точку D,
то работа сил электрического поля
по-прежнему будет равна
Таким образом, работа сил однородного электрического поля при перемещении электрического заряда по прямой BD и по ломаной BCD одинакова и равна произведению электрического заряда на напряженность электрического поля и расстояние, на которое переместился заряд вдоль линии напряженности электрического поля:
Любую кривую, соединяющую точки B и D в однородном электрическом поле, можно приближенно представить состоящей из последовательных отрезков, расположенных параллельно и перпендикулярно линиям напряженности. Применив такие же рассуждения для каждого участка траектории, получим, что полученное для работы выражение справедливо для вычисления работы сил однородного электрического поля при движении заряда по любой траектории.
|
. ПОТЕНЦИАЛ
Основными величинами, характеризующими каждую точку электрического поля, являются потенциал и напряженность поля.
При внесении электрического заряда в электрическое поле приходится затрачивать определенную работу на преодоление сил этого поля.
Величина, определяющая запас энергии (потенциальную энергию) единицы количества электричества, находящейся в данной точке электрического поля, называется потенциалом.
Потенциал данной точки электрического поля численно равен работе, затрачиваемой на внесение заряда в один кулон из бесконечности в эту точку поля. Эта работа равна потенциальной энергии, которой обладает заряд в один кулон в рассматриваемой точке поля.
Таким образом,
![]()
Работа А сил электрического поля определяется произведением силы на путь
А=FS,
где F— сила, н,
S — путь, м,
А — работа, н-м,
q — количество электричества, к.

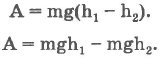


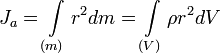 ,
,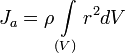
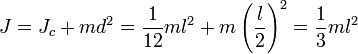
 ,
движущуюся по окружности радиусом
,
движущуюся по окружности радиусом
 .
Пусть на нее действует постоянная
сила, направленная по касательной к
окружности.
.
Пусть на нее действует постоянная
сила, направленная по касательной к
окружности.

 или
или
 .
Используя соотношение связи
тангенциального ускорения с угловым
ускорением
.
Используя соотношение связи
тангенциального ускорения с угловым
ускорением
 ,
получим
,
получим
 .
. :
:
 .
. .
В правой части последнего уравнения
присутствует момент инерции материальной
точки:
.
В правой части последнего уравнения
присутствует момент инерции материальной
точки:
 .
Таким
образом,
.
Таким
образом,
 или
или
 (9.2)
(9.2)
 и
и
 (сила Кулона):
(сила Кулона): ,
, —
радиус-вектор, соединяющий заряды,
0 —
электрическая постоянная.
—
радиус-вектор, соединяющий заряды,
0 —
электрическая постоянная. ,
, - сила, действующая на него со стороны
поля.
- сила, действующая на него со стороны
поля. .
. :
поток вектора напряженности
электрического поля через произвольную
замкнутую поверхность
:
поток вектора напряженности
электрического поля через произвольную
замкнутую поверхность .
.
 - объемная плотность электрического
заряда).
- объемная плотность электрического
заряда). .
. .
. ,
причем вектор
,
причем вектор
 направлен от отрицательного заряда
диполя к положительному.
направлен от отрицательного заряда
диполя к положительному. .
. - потенциал в точке нахождения
заряда qi , созданный
всеми остальными зарядами.
- потенциал в точке нахождения
заряда qi , созданный
всеми остальными зарядами. ,
, - потенциал, создаваемый всеми зарядами
системы в месте нахождения заряда
- потенциал, создаваемый всеми зарядами
системы в месте нахождения заряда
 .
. .
.