Билет 23

Для осуществления вынужденных колебаний в электрическом колебательном контуре в него нужно включить источник электрической энергии,, ЭДС которого изменяется с течением времени по гармоническому закону: ε=ε_mcosωt .

В электротехнике источник электрической энергии, характеризующийся ЭДС и внутренним электрическим сопротивлением r, называется источником ЭДС (источником напряжения)

Если внутреннее сопротивление r источника ЭДС считается пренебрежимо малым по сравнению с R, то такой источник ЭДС называется идеальным.

Уравнение колебательного контура, содержащего последовательно соединенные конденсатор С, активное сопротивление R, катушку индуктивности L и внешнюю переменную ЭДС ε, в сравнении с формулой имеет вид

Для силы тока в контуре при установившихся колебаниях запишем где амплитуда тока I_m = ωq_m = ε_m /Z ; ϕ =ψ –π/2 – сдвиг по фазе между током и внешней ЭДС ε . Величина Z называется полным электрическим сопротивлением (импедансом) цепи: где Х – реактивное сопротивление цепи; X_C =1 (ω_C) – емкостное сопротивление цепи; X_L = ω_L – индуктивное сопротивление цепи

В контуре с внешней ЭДС возможны резонансы напряжений, токов и зарядов. чем меньше R, тем меньше β и больше Q, и при прочих равных условиях тем больше и «острее» максимум при резонансе. Чем больше добротность осциллятора, тем уже резонансная кривая.

Билет 24

Переменным током называются вынужденные колебания тока в цепи, совпадающие с частотой вынуждающей ЭДС. установившиеся вынужденные колебания можно рассматривать как протекание переменного тока в цепи с C, L, R, обусловленное переменным напряжением: U =U_m cos ωt. Уравнение вынужденных колебаний можно переписать в виде Таким образом, сумма падений напряжения на отдельных элементах контура в каждый момент времени равна напряжению, приложенному извне.

Рассмотрим, как соотносятся U и I на элементах контура для сопротивления R (UR ), конденсатора С (UC ) и катушки L (UL): напряжение на емкости UC отстает по фазе от силы тока на π/2 , напряжение на индуктивности UL – опережает на π\2 , а напряжение на активном сопротивлении UR совпадает по фазе с током. Следовательно, понятие добротности показывает, во сколько раз напряжение на конденсаторе может превысить приложенное извне напряжение: Это свойство контуров настраиваться на резонансное напряжение используют для выделения из сложного напряжения нужной составляющей подбором С и L. Так делается при настройке радиоприемников, когда необходимо добиться совпадения собственной частоты колебательного контура приемника с

частотой электромагнитных волн, излучаемых радиостанцией.

Билет 25

Когда колебательный контур содержит последовательно соединенные конденсатор С, катушку индуктивности L и активное сопротивление R, то его уравнение может быть записано как Величину β называют коэффициентом затухания. В этом случае, поскольку R ≠ 0, свободные колебания в контуре будут затухающими. При затухающих свободных колебаниях кроме взаимных превращений энергии электрического и магнитного полей будет происходить преобразование части энергии в джоулево тепло на активном сопротивлении R. Поэтому энергия, запасенная в реальном контуре, постепенно расходуется на нагревание

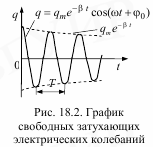. Можно показать, что при β < ω0 решение однородного дифференциального уравнения имеет вид – частота затухающих колебаний; qт и φ0 – произвольные постоянные, определяемые из начальных условий.. Эта функция определяет затухающие колебания и является непериодической. Множитель в уравнении (18.12) называют амплитудой затухающих колебаний. Величину Т = 2π/ω называют периодом затухающих колебаний: где Т0 – период свободных незатухающих колебаний.

Зная зависимость q(t), можно найти напряжение на конденсаторе и ток в контуре. Напряжение на конденсаторе определяется как ток в контуре как где угол δ (π/2 < δ < π ) такой, что Это означает, что при наличии активного сопротивления R колебания тока в контуре опережают по фазе колебания заряда на конденсаторе более чем на π/2. Заметим, что при R = 0 опережение δ = π/2.

величины, характеризующие затухание:

1. Время релаксации τ – это время, за которое амплитуда колебаний уменьшается в е раз, определяется коэффициентом затухания τ =1/β

2. Логарифмический декремент затухания λ определяется как натуральный логарифм отношения двух значений амплитуд, взятых через период колебания Т:

3. Добротность Q колебательного контура равна Чем меньше затухание, тем больше Q. При малых затуханиях (β << ω0) согласно формуле добротность вычисляется так Также в случае слабого затухания справедлива следующая формула для Q: где W – энергия, запасенная в контуре; δW – уменьшение этой энергии за период колебания Т; δW/W – относительное уменьшение энергии за период.

При β ≥ ω0 вместо колебаний будет происходить апериодический разряд конденсатора. Активное сопротивление контура, при котором наступает апериодический процесс, называют критическим