Определение минимального коэф-та смещения. Два вида геометрического расчета зубчатых колес при смещении (дано: 1)z1, z2, m, α, x1, x2; 2)z1, z2, m, α, αW).

PBPN, PBsin=(h_a^*–X)m, PB=mz/2 sin, (h_a^*–X)m/sinmz/2  sin,

h_a*–z/2 sin²  X, X_min=h_a^*[1–z/ (2h_a^*/

/sin²)]. Минимальное число зубьев , своб. от подрезания равно 17, , X_min = h_a^*(z_min–z)/z_min, т.к. h_a^*=1, то X_min=(z_min-z)/z_min = (17-z)/17.

Расчет зубчатых колес

1) α_W – угол зацепления, α – угол рейки. inv α_W = inv α + 2x_Σtgα/(z₁+z₂), inv α_W = tg α_W – α_W (инвалюта). a_W – межосевое расстояние при смещении, a – межосевое расстояние без смещения. a_W=acosα/cosα_W, a=r₁+ r₂, r₁ – радиус делительной окружности шестерни, r₂ – радиус делительной окружности зубчатого колеса. a=r₁+r₂=(m/2)(z₁+z₂). y – коэф-т воспринимаемого смещения. ym=α_W-a, y=(α_W-a)/m. Δy – коэф-т уравнительного смещения.

½mz₁+½mz₂+ym=½mz₁+(h_a^*+x₁+y)m+

+ ½mz₂–(h_a^*–x₂+c^*)m+c^*m

a_W=r₁+r₂+ym, a_W=r_1a+r_f2+c^*m,

сократив одинаковые выражения в левой и правой частях уравнения и разделив все на m, получим: y=x₁+x₂-Δy x₁+x₂=x_Σ – суммарный коэф-т смещения, Δy= x_Σ–y

2) a_W = a∙cosα/cosα_W,

α_W = arccos(a∙cosα/a_W),

inv α_W = inv α + 2x_Σtgα/(z₁+z₂)

x_Σ=(invα_W – invα)(z₁+z₂)/2tgα

y=(α_W-a)/m. Δy= x_Σ–y

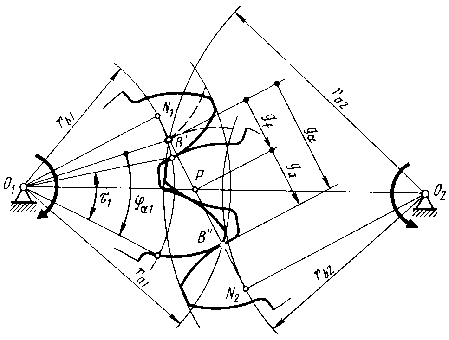
Коэф-т перекрытия. Определение его графическим и аналитическим методами.

Коэф-т перекрытия определяет плавность работы зубчатой передачи и показывает среднее значение числа пар сопряжения зубьев, находящихся в сопряжении. Такие качества передачи обеспечиваются перекрытием работы одной пары зубьев работой другой пары. Для этого каждая последующая пара зубьев должна войти в зацепления еще до того, как предшествующая пара выйдет из зацепления. E=B₁B₂/πmcosα, πm – шаг по делительной окружности, πmcosα – шаг по основной окружности, B₁B₂ – часть линии зацепления ограничительной окружности вершин зубьев шестерни зубчатого колеса, которая называется активной частью линии зацепления.

Аналитический метод. B₁B₂=B₁P+PB₂=B₁N₁–PN₁+BN₂–PN₂=

=√(r²_a1–r²_b1)+√(r²_a2–r²_b2)–N₁N₂,

N₁N₂= r_W1sinα_W+r_W2sinα_W=a_Wsinα_W

r_W1, r_W2 – радиусы начальных окруж.

E > 0 должно быть всегда. Для обычных передач Е ≈ 1,3. Чем больше число зубьев, тем больше Е.

Графический метод

О величине перекрытия судят по коэффициенту перекрытия, который выражают отношением угла торцового перекрытия к угловому шагу. Угол торцового зацепления  – это угол поворота колеса от положения зубьев при входе в зацепление. Следовательно, Е = _а1/₁, где ₁=2/z₁– угловой шаг.

Если Е<1, то непрерывности зацепления зубьев не будет.

Виды смещений. Основной вид смещения при нарезании, уравнительное и воспринимаемое смещения.

1) смещение равно 0

2) Начальная прямая, которая катится без скольжения в процессе нарезания зубчатых колес Х_m>1  это случай положительного смещения.

3) X_m<0 – случай отрицательного смещения.

начальная прямая

x_Σ – суммарный коэф-т смещения x₁+x₂=x_Σ, y – коэф-т воспринимаемого смещения, Δy – коэф-т уравнительного смещения. Δy= x_Σ–y

Передаточное отношение одно- и многоступенчатых зубчатых

передач с неподвижными