9) Понятие генеральной совокупности и выборк

Основу статистического исследования составляет множество данных, полученных в результате измерения одного или нескольких признаков. Реально наблюдаемая совокупность объектов, статистически представленная рядом наблюдений случайной величины , является выборкой, а гипотетически существующая (домысливаемая) — генеральной совокупностью.Пример. Число наблюдений, образующих выборку, называется объемом выборки. Репрезентативности выборки - полнота и адекватность свойств генеральной совокупности, по отношению к которой эту выборку можно считать представительной. Сплошное наблюдение предусматривает обследование всех единиц изучаемой совокупности, а несплошное (выборочное) наблюдение — только его части.Выборка образует вариационный ряд, если выборочные значения случайной величины упорядочены по возрастанию (ранжированы), значения же признака называются вариантами.

Характеристики выборки:Качественная характеристика выборки – кого именно мы выбираем и какие способы построения выборки мы для этого используем.Количественная характеристика выборки – сколько случаев выбираем, другими словами объём

10) Оценка параметров генеральной совокупности по характеристикам

1)Точечная и интервальная оценка параметра ген.совокупности. Под оценкой понимается любое число, рассчитанное по выборке и характеризующее параметр.

Свойства точ.оценки: Несмещенность – среднее выбор. распределения оценки равно величине параметра. Состоятельность – при увеличении объема выборки оценка приближается к значения измеряемого параметра. Эффективность – чем меньше отличаются оценки, полученные в разных выборках, тем выше эффективность.

Интервальная оценка 2 компонента: Интервал в котором ожидается обнаружить оцениваемый параметр ген.совокупности; Вероятность обнаружения параметра в данном интервале.

2)Осн. параметрами ген. совокупности являются мат. ожидание и дисперсия входящих в нее величин.

.Генеральная средняя.

Генеральной средней называют среднее арифметическое значений признака генеральной совокупности. Если все значения признака различны, то

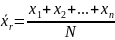
Если значения признака имеют частоты N1, N2, …, Nk, где N1 +N2+…+Nk= N, то

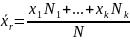
Выборочная средняя.

Выборочной средней называют среднее арифметическое значение признака выборочной совокупности. Если все значения признака выборки различны то

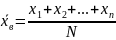
если же все значения имеют частоты n1, n2,…,nk, то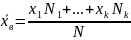

Выборочная дисперсия.

Выборочной дисперсией называют среднее ариф. квадратов отклонения наблюдаемых значений признака от их сред.значения .

Если все значения признака выборки различны, то

если же все значения имеют частоты n1, n2,…,nk, то

Выборочным средним квадратическим отклоненим называют квадратный корень из выборочной дисперсии:

11) Графические характеристики случайных величин. Гистограмма

Гистограмма, , один из видов графического изображения статистического распределении величин по количественному признаку. Г. представляет собой совокупность смежных прямоугольников, построенных на прямой линии. Площадь каждого прямоугольника пропорциональна частоте нахождения данной величины в изучаемой совокупности.

Модой случайной величины называется её наиболее вероятное значение. На рис. А и Б показана мода соответственно для прерывной и непрерывной случайных величин.

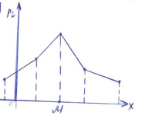
медиана случайной величины – характеристикa для непрерывных случайных величин, хотя формально можно её определить и для прерывной величины. Геометрически медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам

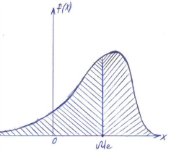
Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.

Если все значения признака выборки различны, то

Если же все значения имеют частоты n1, n2,…,nk, то