Геометрический смысл производной

Пусть функция определена в некоторой окрестности токи , непрерывна в этой точке и , а (рис.2).

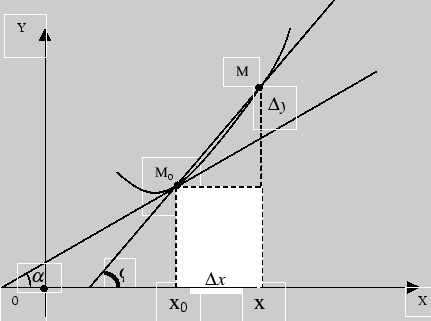
Рис. 2

Придав произвольное приращение аргументу , так чтобы , перейдем к точке с абсциссой и ординатой , где .

Уравнение прямой, проходящей через точки и (секущей графика функции , имеет вид: , где отношение представляет собой угловой коэффициент секущей ( .

Касательной к графику функции в точке называется предельное положение секущей , при стремлении точки по графику к точке .

Для того, чтобы секущая при стремилась к предельному положению, отличному от вертикальной прямой , необходимо и достаточно, чтобы существовал конечный предел , то есть , чтобы существовала конечная производная функции в точке .

Угловой коэффициент касательной получается путем перехода от к пределу при :

Таким образом, получим, что , где - угол наклона касательной к оси (см. рис.), а значение производной равно угловому коэффициенту касательной к графику функции. В этом заключается геометрический смысл производной. Уравнение касательной к графику функции в точке имеет вид

В случае бесконечной производной .

Из уравнения секущей имеем:

Переходя в равенстве к пределу при , получаем уравнение касательной к графику функции в точке в виде , то есть касательная является в данном случае вертикальной прямой, проходящей через точку оси абсцисс.

Механический смысл производной

Пусть материальная точка движется прямолинейно и - длина пути, проходимого за время , отсчитываемого от некоторого момента времени .

Для определения скорости в данный момент придадим переменной некоторое приращение , при этом приращение пути будет равно .

Отношение называется в физике величиной средней скорости движения за промежуток времени, начиная с момента времени , и обозначается

Предел называется величиной мгновенной скорости движения в момент времени .

Таким образом, мгновенная скорость в момент времени прямолинейного движения, совершаемого по закону равна значению производной .

Уравнение касательной к кривой имеет вид:

 

(x-xi)*dY/dx =(y-yi); или (x-xi)*dFy/dt = (y-yi)*dFx/dt;

 

где dY/dx = dF(x)/dx = - (¶F1(x, y)/¶x)/(¶F1(x, y)/¶y);

 

Уравнение нормали к кривой имеет вид:

 

(x-xi) = -(y-yi)*dY/dx; или (x-xi)*dFx/dt = -(y-yi)*dFy/dt;

  

Односторонние производные

Производная есть предел разностного отношения  , причём этот предел не зависит от характера стремления   к нулю ( может быть как больше, так и меньше нуля, то есть может стремиться к нулю как справа, так и слева). Но в ряде случаев функция может не иметь в заданной точке производной, хотя в этой точке существует предел отношения   при условии, что    стремится к нулю только справа (правый предел) или только слева (левый предел), или же существует как правый, так и левый предел, но они не равны друг другу. Например, если функция определена на отрезке, а за пределами этого отрезка не определена, то на границах отрезка могут существовать только односторонние пределы. Такие односторонние пределы называются односторонними производными. А именно, если для рассматриваемой функции в заданной точке существует правый (левый) предел отношения  , то этот предел называется правой (левой) производной. Правая производная функции    обозначается символом  , левая – символом  . То есть ,  . Выше (см. § 7) уже говорилось о том, что функция  y= = 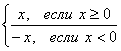 не дифференцируема в точке x = 0.  Однако в этой точке она имеет как правую, так и левую производную. Действительно,  ,  .

Если функция   имеет в точке x производную, то очевидно, что она имеет в этой точке как правую, так и левую производную, причём  .

Верно и обратное утверждение: если функция   имеет в точке x равные между собой правую и левую производную, то она имеет в этой точке и производную, причём

Необходимое условие: Функция y=f(x) имеет производную в точке тогда и только тогда, когда в этой точке существуют и равны между собой производные функции справа и слева. Причем

.