Логарифмические неравенства Определение

Логарифмическим неравенством называется неравенство, в котором неизвестная величина стоит под знаком логарифма.

1. Неравенство   в случае, если   сводится к равносильному неравенству  . Если же   - то к неравенству  .

Аналогично неравенство   равносильно неравенствам для   :  ; для   :  .

Решения полученных неравенств надо пересечь с ОДЗ: 

Пример

Задание. Решить неравенство 

Решение. ОДЗ: 

Учитывая выше написанное, получаем, что заданное логарифмическое неравенство равносильно неравенству:

   или   

В пересечении с ОДЗ получаем, что 

Ответ. 

2. Решение логарифмического неравенства вида   равносильно решению следующих систем:

а)        б) 

Неравенство   в каждом из двух случаев сводится к одной из систем:

а)        б) 

Пример

Задание. Решить неравенство 

Решение. Данное неравенство равносильно системе:

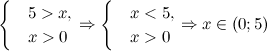
Ответ. 

Переход к новому основанию логарифма

Гипермаркет знаний>>Математика>>Математика 10 класс>> Переход к новому основанию логарифма

§ 53. Переход к новому основанию логарифма

Логарифмических функций бесконечно много:  и т.д. Возникает вопрос, как они связаны между собой? Есть ли, например, какая-то связь между функциями у=log₂ х и y=log₃x? На рис. 231 изображены графики функций у=log₂ х и у=log₃х. Не кажется ли вам, что график первой функции получается из графика второй функции растяжением от оси х с некоторым коэффициентом к >1. Если наше геометрическое наблюдение верно, то должно выполняться равенство:

Так ли это? На все поставленные вопросы мы ответим в этом параграфе. Теоретической основой для ответа является следующая теорема.

Теперь нетрудно ответить на поставленный выше вопрос: как связаны между собой различные логарифмические функции? Рассмотрим две логарифмические функции у =log₂ х и у =log₃ х, графики которых изображены на рис. 231. Имеем:

Таким образом, наша догадка подтвердилась: действительно, справедливо соотношение

;

подтвердилась и наша догадка о том, что в данном случае к > 1, поскольку log₂ 3 > 1.

Аналогичные формулы связывают и другие логарифмические функции. Например, справедливы соотношения:

Рассмотрим два важных частных случая формулы перехода к новому основанию логарифма, два следствия из доказанной теоремы.

Следствие 1. Если а и b положительные и отличные от 1 числа, то справедливо равенство:

Доказательство. Положив в формуле (1) с =Ь, получим:

Следствие 2. Если а и b — положительные числа, причем  , то для любого числа   справедливо равенство:

Доказательство. Перейдем в выражении   к логарифмам по основанию а: 

Пример 1. Дано:

Решение.

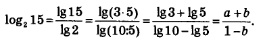
Пример 2. Решить уравнение:

Решение. Перейдем во всех логарифмах к одному основанию 4. Для этого дважды воспользуемся формулой, доказанной в следствии 2:

Теперь заданное уравнение можно переписать в более простой форме:

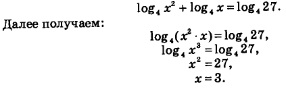
Функция синус

Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная. Функция нечетная: sin(−x)=−sin x для всех х ∈ R.  График функции симметричен относительно начала координат. Функция периодическая с наименьшим положительным периодом 2π: sin(x+2π·k) = sin x, где k ∈ Z для всех х ∈ R. sin x = 0 при x = π·k, k ∈ Z. sin x > 0 (положительная) для всех x ∈ (2π·k, π+2π·k), k ∈ Z. sin x < 0 (отрицательная) для всех x ∈ (π+2π·k, 2π+2π·k), k ∈ Z. Функция возрастает от −1 до 1 на промежутках: Функция убывает от −1 до 1 на промежутках: Наибольшее значение функции sin x = 1 в точках: Наименьшее значение функции sin x = −1 в точках: