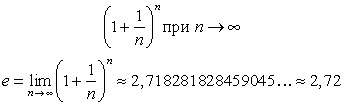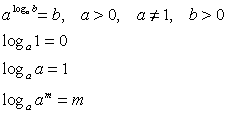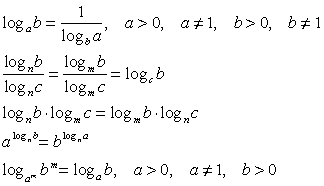- •Рациональное число как десятичная дробь
- •Периодическая дробь
- •Приближенные значения числа . Свойство абсолютной величины суммы
- •1.Понятие комплексного числа
- •2.Геометрическая интерпретация
- •3.Модуль комплексного числа
- •4.Сложение и умножение комплексных чисел
- •5.Вычитание и деление комплексных чисел
- •6.Тригонометрическая форма
- •7.Свойства модуля и аргумента
- •8.Возведение в степень и извлечение корня
- •Понятие корня степени n
- •Понятие арифметического корня степени n
- •Поятие степени с рациональным показателем
- •Степень с действительным показателем
- •Решение простейших показательных уравнений.
- •Решение простых показательных уравнений. Примеры.
- •Замена переменной в решении показательных уравнений. Примеры.
- •Показательные неравенства: примеры и достаточные знания, необходимые для решения заданий
- •Логарифмы
- •Основные свойства логарифмов
- •Сложение и вычитание логарифмов
- •Вынесение показателя степени из логарифма
- •Переход к новому основанию
- •Основное логарифмическое тождество
- •Логарифмическая единица и логарифмический ноль
- •Что такое логарифмическое уравнение?
- •Как решать логарифмические уравнения?
- •Логарифмические неравенства Определение
- •Переход к новому основанию логарифма
- •§ 53. Переход к новому основанию логарифма
- •Функция синус
- •Функция косинус
- •Функция тангенс
- •Функция котангенс
- •Знаки тригонометрических функций
- •Тема 16. "Простейшие тригонометрические неравенства".
- •Основные понятия и свойства функций
- •Экстремумы функции
Показательные неравенства: примеры и достаточные знания, необходимые для решения заданий
Пример. Решите
неравенство 22x+1−7![]() 10x+52x+1
10x+52x+1![]() 0
0
Решение: 22x+1−7
10x+52x+1
0![]() 22x
2−7
22x
2−7
![]() 2
5
2
5![]() x+52x
5
0
т.к 5x
x+52x
5
0
т.к 5x![]() 0 ,
то можно разделить на
5x
2
0 обе
части неравенства 2
2x
2−7
2
5
x+5
5x
2
0 ,
получим
0 ,
то можно разделить на
5x
2
0 обе
части неравенства 2
2x
2−7
2
5
x+5
5x
2
0 ,
получим ![]() 5x
5x![]() 22
22![]() 2x
2−
5x
27
2
5
x+
5x
25
5x
2
0
2
5x2x
2−7
5x2x+5
0 .
Пусть y=
52
x ,
тогда получим систему
52
x
2x
2−
5x
27
2
5
x+
5x
25
5x
2
0
2
5x2x
2−7
5x2x+5
0 .
Пусть y=
52
x ,
тогда получим систему
52
x![]() y
0
2y2−7y+5
0 .
Решая уравнение 2y2−7y+5=0 получим
корни y1=1
y1=25.
Решением системы будет 1
y
25.
Вернемся к замене 1
52
x
25 и
решим
систему
y
0
2y2−7y+5
0 .
Решая уравнение 2y2−7y+5=0 получим
корни y1=1
y1=25.
Решением системы будет 1
y
25.
Вернемся к замене 1
52
x
25 и
решим
систему ![]() 52
x
52
x![]() 1
52
x
25
1
52
x
25![]()
![]()
![]()
![]()
![]() 0
0![]() 52
1
x
0
x
−1
x
52
1
x
0
x
−1
x![]()
![]() −1;0
−1;0![]()
Ответ: x −1;0
Для решения используем последовательно знания следующих свойств:
Свойство произведения степеней с одинаковыми основаниями: am+n=am an
Свойство степени, основанием которой является степень: am n= am n= an m a 0
Свойство степени произведения положительных чисел: a b n=an bn a 0 b 0
Свойство равносильности неравенств: f(x) g(x) mf(x) mg(x) m 0
Свойство частного степеней с одинаковыми показателями степени: bnan= ba n a 0 b 0
Основное свойство дроби: ba=b:ma:m=b ka k m k
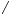 =0
=0Свойство степени с нулевым показателем: a0=1 a =0
Свойство степени с отрицательным показателем: ba −n= ab n n Z
Свойство равносильности показательных неравенств: af(x) ag(x)
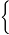 0
a
1
f(x)
g(x)
0
a
1
f(x)
g(x)
Свойство равносильности показательных неравенств: af(x) ag(x) 0 a 1 f(x) g(x)
Логарифмы
Определение логарифма Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести а, чтобы получить b.
Числом е в математике принято обозначать предел, к которому стремиться выражение
Число е является иррациональным числом — числом, несоизмеримым с единицей, оно не может быть точно выраженным ни целым ни дробным рациональным числом. Буква е — первая буква латинского слова exponere — выставлять напоказ, отсюда в математике названиеэкспоненциальная — показательная функция. Число е широко применяется в математике, и во всех науках, так или иначе применяющих для своих нужд математические расчеты. Свойства логарифма
Действия с логарифмами
|
||||||||||||||||||||
|