Понятие арифметического корня степени n
Если 
и n -
натуральное число, большее 1,
то существует, и только одно, неотрицательное
число х,
такое, что выполняется равенство 
.
Это число хназывается
арифметическим корнем n-й
степени из неотрицательного числа а и
обозначается
.
Число а называется
подкоренным числом, n -
показателем корня.
Итак,
согласно определению запись 
,
где
,
означает, во-первых, что
и,
во-вторых, что
,
т.е. 
.
Поятие степени с рациональным показателем
Степень
с натуральным показателем: пусть а -
действительное число, а n -
натуральное число, большее единицы, n-й
степенью числа а называют
произведениеn множителей,
каждый из которых равен а,
т.е. 
.
Число а -
основание степени, n -
показатель степени. Степень с нулевым
показателем: полагают по определению,
если 
,
то 
.
Нулевая степень числа 0 не
имеет смысла. Степень с отрицательным
целым показателем: полагают по определению,
если
и n -
натуральное число, то 
.
Степень с дробным показателем: полагают
по определению, если 
и n -
натуральное число, m -
целое число, то 
Степенью
числа а > 0 с рациональным
показателем 
,
где m – целое число, а n – натуральное
(n > 1), называется число 
Итак, 
Например, 
Степень числа 0 определена только для положительных показателей;
по определению 0r = 0 , для любого r > 0
Замечания
Из определения степени с рациональным показателем следует, что для любого положительного а и любого рационального r число ar положительно.
Любое рациональное число допускает различные записи его в виде дроби, поскольку
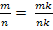для
любого натурального k. Значение аr также
не зависит от формы записи рационального
числа r.При а < 0 рациональная степень числа а не определяется.
Степень с действительным показателем
Пусть
дано положительное число 
и
произвольное действительное число 
.
Число 
называется
степенью, число
—
основанием степени, число
—
показателем степени.
По определению полагают:
.
.
, 
.
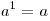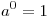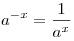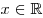Если
и 
—
положительные числа, 
и 
—
любые действительные числа, то справедливы
следующие свойства: