• Округление к меньшему по модулю (округление к нулю, целое англ. fix, truncate, integer) — самое «простое» округление, поскольку после обнуления «лишних» знаков предшествующий знак сохраняют. Например, 11,9 → 11; −0,9 → 0; −1,1 → −1).

• Округление к большему (округление к +∞, округление вверх, англ. ceiling) — если обнуляемые знаки не равны нулю, предшествующий знак увеличивают на единицу, если число положительное, или сохраняют, если число отрицательное. В экономическом жаргоне —округление в пользу продавца, кредитора (лица, получающего деньги). В частности, 2,6 → 3, −2,6 → −2.

• Округление к меньшему (округление к −∞, округление вниз, англ. floor) — если обнуляемые знаки не равны нулю, предшествующий знак сохраняют, если число положительное, или увеличивают на единицу, если число отрицательное. В экономическом жаргоне —округление в пользу покупателя, дебитора (лица, отдающего деньги). Здесь 2,6 → 2, −2,6 → −3.

• Округление к большему по модулю (округление к бесконечности, округление от нуля) — относительно редко используемая форма округления. Если обнуляемые знаки не равны нулю, предшествующий знак увеличивают на единицу.

• .Модуль действительного числа

• и его свойства В младших классах вы уже встречались с понятием модуля (или абсолютной величины) числа, пользовались обозначением | а |. Вы знаете, что, например, | 5 | = 5, | - 3 | = 3. Правда, раньше речь шла только о рациональных числах. Теперь надо ввести понятие модуля для любого действительного числа.

• Определение. Модулем неотрицательного действительного числа х называют само это число: | х | = х; модулем отрицательного действительного числа х называют противоположное число: I х | = - х.

• Короче это записывают так:

• Например,

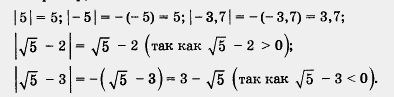• На практике используют различные свойства модулей, например:

• 1. |а|  0.  2.|аb| =|a| |b|.  2. Геометрический смысл модуля действительного числа

• Вернемся к множеству R действительных чисел и его геометрической модели — числовой прямой. Отметим на прямой две точки а и b (два действительных числа а и b), обозначим через   (a, b) расстояние между точками а и b (  — буква греческого алфавита «ро»). Это расстояние равно b - а, если b > а (рис. 101), оно равно а - b, если а > b (рис. 102), наконец, оно равно нулю, если а = b. 

• Все три случая охватываются одной формулой: 

• Пример 1. Решить уравнения:

• а) | х - 2| = 3; б) | х + 3,2| = 2; в) | х | = 2,7; г) | x -   I = 0.  Решение, а) Переведем аналитическую модель |х - 2| = 3 на геометрический язык: нам нужно найти на координатной прямой такие точки х, которые удовлетворяют условию   (х, 2) = 3, т. е. удалены от точки 2 на расстояние, равное 3. Это — точки - 1 и 5 (рис. 103). Следовательно, уравнение имеет два корня: - 1 и 5.

• б) Уравнение | х + 3,2 | = 2 перепишем в виде | х - (— 3,2) | = 2 и далее   (х, - 3,2) = 2. На координатной прямой есть две точки, которые удалены от точки - 3,2 на расстояние, равное 2. Это — точки - 5,2 и - 1,2 (рис. 104). Значит, уравнение имеет два корня: -5,2 и - 1,2. 

• в) Уравнение |x| = 2,7 перепишем в виде |х - 0| = 2,7, или, что то же самое,   (х, 0) = 2,7. На координатной прямой имеются две точки, которые удалены от точки О на расстояние, равное 2,7. Это — точки - 2,7 и 2,7 (рис. 105). Таким образом, уравнение имеет два корня: - 2,7 и 2,7'.

• г) Для уравнения |х -  | = 0 можно обойтись без геометрической иллюстрации, ведь если | а | = 0, то а = 0. Поэтому х -   = 0, т. е. х =   .

• Пример 2. Решить уравнения:

• а) |2х - 6| = 8; б) |5 - Зx | = 6; в) |4x + 1| = - 2.

• Р е ш е н и е.

• а) Имеем|2x - 6| = |2(x -3)| =|2|.| = 2|x -3|

• Значит, заданное уравнение можно преобразовать к виду

• 2|х - 3| = 8, откуда получаем | х - 3| = 4.

• Переведем аналитическую модель | х - 3 | = 4 на геометрический язык: нам нужно найти на координатной прямой такие точки х, которые удовлетворяют условию   (х, 3) = 4, т. е. удалены от точки 3 на расстояние, равное 4. Это — точки - 1 и 7 (рис. 106). Итак, уравнение имеет два корня: - 1 и 7.

• б) Имеем

• Поэтому заданное уравнение можно преобразовать к виду

• Переведем аналитическую модель   на геометрический язык: нам нужно найти на координатной прямой такие точки х, которые удовлетворяют условию 

• Значит, они удалены от точки   , на расстояние, равное 2.

• в) Для уравнения  | 4х + 1 | = - 2 никаких преобразований делать не нужно. Оно явно не имеет корней, поскольку в левой его части содержится неотрицательное выражение, а в правой — отрицательное число.

• Пример 3. Построить график функции у = |х + 2 |.

• Решение. График этой функции получается из графика функции у = | х | сдвигом последнего на две единицы масштаба влево (рис. 111).

• 4. Тождество  Мы знаем, что если  .А как быть, если а < 0? Написать у   в этом случае нельзя, ведь а < 0 и получится, что  , а это неверно, так как значение квадратного корня не может быть отрицательным.

• Чему же равно выражение  при а < 0? По определению квадратного корня в ответе должно получиться такое число, которое, во-первых, положительно и, во-вторых, при возведении в квадрат дает подкоренное число, т. е. а². Таким числом будет - а. Смотрите:

• 1) - а > 0 (еще раз напомним, что а — отрицательное число, значит, - а — положительное число);

• 2)(-а)²=а².

• Итак,

• Вам ничего не напоминает конструкция, полученная в правой части равенства? Вспомните, ведь точно так же определяется модуль числа а:

• Значит,  и | а | — одно и то же. Тем самым мы доказали важное тождество:

• В роли а может выступать любое числовое или алгебраическое выражение.

• Пример 4. Упростить выражение   , если:  а) а - 1 > 0; б) а - 1 < 0.  Решение. Как мы только что установили, справедливо тождество

• а) Если а - 1 > 0, то | а - 1| = а - 1. Таким образом, в этом случае получаем   = а - 1.  б) Если а - 1 <0, то |а - 1| = -(а - 1) = 1 - а. Значит, в этом случае получаем   = 1 - а. в

• 

• основанием для того, чтобы вводить в математику новые числа.Оказалось, что если производить вычисления по обычным правилам над выражениями,в которых встречаются квадратный корень из отрицательного числа, то можно прийти к результату,уже не содержащему квадратный корень из отрицательного числа. В XVIв. Кардано нашел формулу для решения кубического уравнения.Оказалось,когда кубическое уравнение имеет три действительных корня, в формуле Кардано встречается квадратный корень из отрицательного числа. Поэтому квадратные корни из отрицательных чисел стали употреблять в математике и назвали их мнимыми числами– тем самым они как бы приобрели право на нелегальное существование.Полные гражданские права мнимым числам дал Гаусс, который назвал их комплексными числами, дал геометрическую интерпретацию и доказал основную теорему алгебры,утверждающую,что каждый многочлен имеет хотя бы один действительный корень.

• 1.Понятие комплексного числа

• Решение многих задач математики,физики сводится к решению алгебраических уравнений.Поэтому исследование алгебраических уравнений является одним из важнейших вопросов в математике.Стремление сделать уравнения разрешимыми– одна из главных причин расширения понятия числа.

• Так для решимости уравнений вида X+A=B положительных чисел недостаточно.Например, уравнение X+5=2 не имеет положительных корней. Поэтому приходится вводить отрицательные числа и нуль.

• На множестве рациональных чисел разрешимы алгебраические уравнения первой степени,т.е. уравнения вида A·X+B=0 (A 0). Однако алгебраические уравнения степени выше первой могут не иметь рациональных корней. Например,такими являются уравненияX²=2, X³=5.Необходимость решения таких уравнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел.

• Однако и действительных чисел недостаточно для того, чтобы решить любое алгебраическое уравнение.Например, квадратное уравнение с действительными коэффициентами и отрицательным дискриминантом не имеет действительных корней. Простейшее из них – уравнениеX²+1=0.Поэтому приходится расширять множество действительных чисел, добавляя к нему новые числа. Эти новые числа вместе с действительными числами образуют множество,которое называют множествомкомплексных чисел.

• Выясним предварительно,какой вид должны иметь комплексные числа. Будем считать, что на множестве комплексных чисел уравнениеX²+1=0имеет корень.Обозначим этот корень буквойiТаким образом,i– это комплексное число, такое,что i²=–1.

• Как и для действительных чисел, нужно ввести операции сложения и умножения комплексных чисел так, чтобы сумма и произведение их были бы комплексными числами.Тогда, в частности, для любых действительных чисел AиBвыражениеA+B·iможно считать записью комплексного числа в общем виде. Название«комплексное»происходит от слова «составное»:по виду выраженияA+B·i.

• Комплексными числами называют выражения видаA+B·i,где Aи B–действительные числа, а i– некоторый символ, такой что i²=–1, и обозначают буквой Z.

• Число Aназывается действительной частью комплексного числа A+B·i,а число B– его мнимой частью. Числоiназывается мнимой единицей.

• Например,действительная часть комплексного числа 2+3·iравна 2, а мнимая равна 3.

• Для строгого определения комплексного числа нужно ввести для этих чисел понятие равенства.

• Два комплексных числа A+B·iи C+D·iназываютсяравнымитогда и только тогда, когдаA=Cи B=D,т.е. когда равны их действительные и мнимые части.

• 2.Геометрическая интерпретация

• КОМПЛЕКСНОГО ЧИСЛА

• 

• Рисунок 1

• Действительные числа геометрически изображаются точками числовой прямой. Комплексное число A+B·iможно рассматривать как пару действительных чисел(A;B).Поэтому естественно комплексное число изображать точками плоскости.В прямоугольной системе координат комплексное число Z=A+B·iизображается точкой плоскости с координатами(A;B),и эта точка обозначается той же буквойZ (рисунок 1). Очевидно,что получаемое при этом соответствие является взаимно однозначным.Оно дает возможность интерпретировать комплексные числа как точки плоскости на которой выбрана система координат.Такая координатная плоскость называетсякомплексной плоскостью.Ось абсцисс называетсядействительной осью, т.к.на ней расположены точки соответствующие действительным числам. Ось ординат называется мнимой осью – на ней лежат точки,соответствующие мнимым комплексным числам.

• 

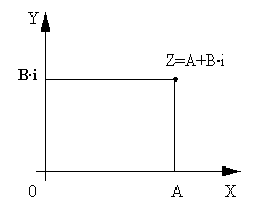
• Рисунок 2

• Не менее важной и удобной является интерпретация комплексного числа A+B·i как вектора, т.е.вектора с началом в точке

• O(0;0)и с концом в точке М(A;B) (рисунок 2).

• Соответствие установленное между множеством комплексных чисел, с одной стороны, и множествами точек или векторов плоскости, с другой, позволяет комплексные числа точками или векторами.

• 3.Модуль комплексного числа

• Пусть дано комплексное число Z=A+B·i.СопряженнымсZназывается комплексное числоA –B·i,которое обозначается ,т.е.

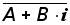• = =A–B·i.

• Отметим, что =A+B·i,поэтому для любого комплексного числа Zимеет место равенство =Z.

• Модулемкомплексного числа Z=A+B·iназываетсячисло и обозначается ,т.е.

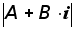• = = (1)

• Из формулы(1) следует, что для любого комплексного числа Z,причем =0тогда и только тогда, когда Z=0,т.е. когда A=0иB=0. Докажем,что для любого комплексного числа Zсправедливы формулы:

• 

• 4.Сложение и умножение комплексных чисел

• Суммойдвух комплексных чисел A+B·iи C+D·iназывается комплексное число (A+C)+(B+D)·i,т.е. (A+B·i)+(C+D·i)=(A+C)+(B+D)·i

• Произведениемдвух комплексных чиселA+B·iи C+D·iназывается комплексное число (A·C– B·D)+(A·D+B·C) ·i,т.е.

• (A+B·i)·(C+D·i)=(A·C– B·D)+(A·D+B·C)·i

• Из формул вытекает, что сложение и умножение можно выполнять по правилам действий с многочленами,считая i²=–1.Операции сложения и умножения комплексных чисел обладают свойствами действительных чисел. Основные свойства:

• Переместительное свойство:

• Z₁+Z₂=Z₂+Z₁, Z₁·Z₂=Z₂·Z₁

• Сочетательное свойство:

• (Z₁+Z₂)+Z₃=Z₁+(Z₂+Z₃), (Z₁·Z₂)·Z₃=Z₁·(Z₂·Z₃)

• Распределительное свойство:

• Z₁·(Z₂+Z₃)=Z₁·Z₂+Z₁·Z₃

• Геометрическое изображение суммы комплексных чисел

• 

• Рисунок 3

• Согласно определению сложения двух комплексных чисел, действительная часть суммы равна сумме действительных частей слагаемых,мнимая часть суммы равна сумме мнимых частей слагаемых.Точно также определяются координаты суммы векторов:

• Сумма двух векторов с координатами(A₁;B₁)и (A₂;B₂)есть вектор с координатами(A₁+A₂;B₁+B₂).Поэтому, чтобы найти вектор,соответствующий сумме комплексных чисел Z₁и Z₂нужно сложить векторы, соответствующие комплексным числам Z₁и Z₂.

• Пример1: Найти сумму и произведение комплексных чисел Z₁=2– 3Чi и

• 1Способ:

• Z₂=–7 + 8Чi.

• Z₁+ Z₂= 2 – 7 + (–3 + 8)Чi = –5 + 5Чi

• 

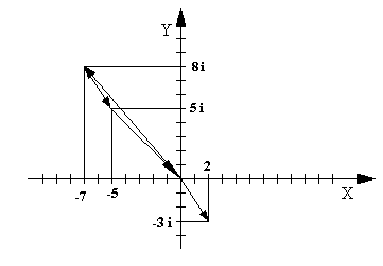
• Z₁ЧZ₂= (2 – 3Чi)Ч(–7 + 8Чi) = –14 + 16Чi+ 21Чi+ 24 = 10 + 37Чi

• 2 Способ:

• 5.Вычитание и деление комплексных чисел

• Вычитание комплексных чисел – это операция, обратная сложению:для любых комплексных чиселZ₁и Z₂существует,и притом только одно, число Z,такое, что:

• Z + Z₂=Z₁

• Если к обеим частям равенства прибавить (–Z₂)противоположное числу Z₂:

• Z+Z₂+(–Z₂)=Z₁+(–Z₂),откуда

• Z = Z₁–Z₂

• Число Z=Z₁+Z₂называют разностью чисел Z₁и Z₂.

• Деление вводится как операция, обратная умножению:

• ZЧZ₂=Z₁

• Разделив обе части наZ₂получим:

• Z=

• Из этого уравнения видно, что Z₂ 0

• 

• Геометрическое изображение разности комплексных чисел

• Рисунок 4

• РазностиZ₂–Z₁комплексных чисел Z₁и Z₂,соответствует разность векторов,соответствующих числам Z₁и Z₂.Модуль разности двух комплексных чисел Z₂и Z₁по определению модуля есть длина вектораZ₂– Z₁.Построим этот вектор, как сумму векторовZ₂и (–Z₁) (рисунок 4). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости,которые соответствуют этим числам.

• Это важное геометрическое истолкование модуля разности двух комплексных чисел позволяет с успехом использовать простые геометрические факты.

• Пример 2:Даны комплексные числа Z₁= 4 + 5·iи Z₂= 3 + 4·i.Найти разность Z₂– Z₁и частное

• Z₂– Z₁= (3 + 4·i)– (4 + 5·i) = –1 – i

• = =

• 6.Тригонометрическая форма

• КОМПЛЕКСНОГО ЧИСЛА

• 

• Рисунок 5

• Запись комплексного числа Zв виде A+B·iназываетсяалгебраической формойкомплексного числа. Помимо алгебраической формы используются и другие формы записи комплексных чисел.

• Рассмотримтригонометрическую формузаписи комплексного числа. Действительная и мнимая части комплексного числа Z=A+B·iвыражаются через его модуль =r и аргумент jследующим образом:

• A= r·cosj; B= r·sinj.

• Число Zможно записать так:

• Z= r·cosj+i· ·sinj= r·(cosj+i·sinj)

• Z = r·(cosj+i·sinj) (2)

• Эта запись называетсятригонометрической формой комплексного числа.

• r = –модуль комплексного числа.

• Число jназывают аргументом комплексного числа.

• Аргументом комплексного числа Z 0называется величина угла между положительным направлением действительной оси и векторомZ, причем величина угла считается положительной,если отсчет ведется против часовой стрелки,и отрицательной,если производится по часовой стрелке.

• Для числаZ=0аргумент не определяется,и только в этом случае число задается только своим модулем.

• Как уже говорилось выше =r = ,равенство (2)можно записать в виде

• A+B·i= ·cosj+i· ·sinj,откуда приравнивая действительные и мнимые части,получим:

• cosj= , sinj= (3)

• Если sinjподелить наcosjполучим:

• tgj= (4)

• Эту формулу удобней использовать для нахождения аргумента j,чем формулы(3). Однако не все значенияj,удовлетворяющие равенству (4),являются аргументами числа A+B·i.Поэтому при нахождении аргумента нужно учесть, в какой четверти расположена точка A+B·i.

• 7.Свойства модуля и аргумента

• КОМПЛЕКСНОГО ЧИСЛА

• С помощью тригонометрической формы удобно находить произведение и частное комплексных чисел.

• Пусть Z₁= r₁·(cosj₁+i·sinj₁),Z₂= r₂·(cosj₂+i·sinj₂).Тогда:

• Z₁Z₂= r₁·r₂[cosj₁·cosj₂–sinj₁·sinj₂+i·( sinj₁·cosj₂+ cosj₁·sinj₂)]=

• =r₁·r₂[cos(j₁+ j₂) + i·sin(j₁+ j₂)].

• Таким образом,произведение комплексных чисел, записанных в тригонометрической форме, можно находить по формуле:

• Z₁Z₂= r₁·r₂[cos(j₁+ j₂) + i·sin(j₁+ j₂)](5)

• Из формулы(5) следует, чтопри умножении комплексных чисел их модули перемножаются,а аргументы складываются.

• Если Z₁=Z₂то получим:

• Z²=[r·(cosj+i·sinj)]²=r²·(cos2j+i·sin2j)

• Z³=Z²·Z= r²·(cos2j+i·sin2j)·r·(cosj+i·sinj)=

• =r³·(cos3j+i·sin3j)

• Вообще для любого комплексного числа Z=r·( cosj+i·sinj) 0и любого натурального числа nсправедлива формула:

• Zⁿ=[ r·(cosj+i·sinj)]ⁿ= rⁿ·( cosnj+i·sinnj),(6)

• которую называют формулой Муавра.

• Частное двух комплексных чисел, записанных в тригонометрической форме, можно находить по формуле:

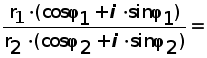
• [cos(j₁– j₂) + i·sin(j₁– j₂)].(7)

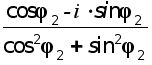• = = cos(–j₂) + i·sin(–j₂)

• Используя формулу 5

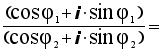• (cosj₁+i·sinj₁)Ч(cos(–j₂) + i·sin(–j₂)) =

• cos(j₁– j₂) + i·sin(j₁– j₂).

• Пример 3:

• Z³= –8

• Число–8запишем в тригонометрической форме

• 8 = 8·( cos(p+ 2pk) + i·sin(p+ 2pk)), kОZ

• ПустьZ = rЧ(cosj+iЧsinj),тогда данное уравнение запишется в виде:

• r³Ч(cos3j+iЧsin3j) = 8·( cos(p+ 2pk) + i·sin(p+ 2pk)), kОZ

• Тогда 3j=p+ 2pk, kОZ

• j= , kОZ

• r³= 8

• r = 2

• Следовательно:

• Z = 2·( cos( ) + i·sin( )), kОZ

• k= 0,1,2...

• k= 0

• Z₁= 2·( cos 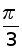+ i·sin ) = 2·( i) = 1+ Чi

• k= 1

• Z₂= 2·( cos( + ) + i·sin( + )) = 2·( cosp+ i·sinp) = –2

• k= 2

• Z₃= 2·( cos( + ) + i·sin( + )) = 2·( cos + i·sin ) = 1– Чi

• Ответ:Z₁₃= ; Z₂= –2

• Пример4:

• Z⁴= 1

• Число1запишем в тригонометрической форме

• 1 = 1·( cos(2pk) + i·sin(2pk)), kОZ

• ПустьZ = rЧ(cosj+iЧsinj),тогда данное уравнение запишется в виде:

• r⁴Ч(cos4j+iЧsin4j) = cos(2pk) + i·sin(2pk)), kОZ

• 4j= 2pk, kОZ

• j= , kОZ

• r⁴= 1

• r = 1

• Z = cos +iЧsin

• k= 0,1,2,3...

• k= 0

• Z₁= cos0+iЧsin0 = 1 + 0 = 1

• k= 1

• Z₂= cos +iЧsin = 0 +i= i

• k= 2

• Z₃= cosp+ i·sinp= –1 + 0 = –1

• k= 3

• Z₄= cos +iЧsin

• Ответ:Z₁₃= 1

• Z₂₄= i

• 8.Возведение в степень и извлечение корня

• Из формулы6 видно, что возведение комплексного числа r·( cosj+i·sinj)в целую положительную степень с натуральным показателем его модуль возводится в степень с тем же показателем,а аргумент умножается на показатель степени.

• [r·(cosj+i·sinj)]ⁿ= rⁿ·( cos nj+i·sin nj)

• Число Zназываетсякорнем степениnиз числа w( обозначается 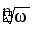),если Zⁿ=w.

• Из данного определения вытекает, что каждое решение уравнения Zⁿ=wявляется корнем степени nиз числа w.Другими словами,для того, чтобы извлечь корень степени nиз числа w,достаточно решить уравнениеZⁿ=w.Если w=0,то при любомnуравнение Zⁿ=wимеет только одно решениеZ=0. Еслиw 0,то и Z 0,а, следовательно,и Zи wможно представить в тригонометрической форме

• Z = r·(cosj+i·sinj), w= p·(cosy+i·siny)

• УравнениеZⁿ=wпримет вид:

• rⁿ·( cos nj+i·sin nj) = p·( cosy+i·siny)

• Два комплексных числа равны тогда и только тогда, когда равны их модули,а аргументы отличаются слагаемыми,кратными 2p.Следовательно, rⁿ= p и nj=y+ 2pk,гдеkОZили r = и j= ,где kОZ.

• Итак, все решения могут быть записаны следующим образом:

• Z_K= [cos( ) +i·sin( )], kОZ (8)

• Формулу 8называют второй формулой Муавра.

• Таким образом,если w 0,то существует ровно nкорней степениnиз числа w:все они содержатся в формуле 8. Все корни степениnиз числа wимеют один и тот же модуль ,но разные аргументы,отличающиеся слагаемым,кратным числу .Отсюда следует,что комплексные числа, являющиеся корнями степениnиз комплексного числа w,соответствует точкам комплексной плоскости,расположенным в вершинах правильного n– угольника,вписанного в окружность радиуса с центром в точке Z = 0.

• Символ не имеет однозначного смысла. Поэтому,употребляя его, следует четко представлять себе, что под этим символом подразумевается.Например, используя запись ,следует подумать о том, чтобы было ясно, понимается под этим символом пара комплексных чисел iи–i, или одно, то какое именно.

• Уравнения высших степеней

• Формула 8определяет все корни двучленного уравнения степени n.Неизмеримо сложнее обстоит дело в случае общего алгебраического уравнения степени n:

• a_nЧZⁿ +a_n–1ЧZ^n–1+...+a₁ЧZ¹+a₀=0(9)

• Где a_n,...,a₀– заданные комплексные числа.

• В курсе высшей математики доказывается теорема Гаусса: каждое алгебраическое уравнение имеет в множестве комплексных чисел по крайней мере один корень.Эта теорема была доказана немецким математиком Карлом Гауссом в 1779 году.

• Опираясь на теорему Гаусса, можно доказать, что левая часть уравнения 9всегда может быть представлена в виде произведения:

• ,

• Где Z₁,Z₂,...,Z_K– некоторые различные комплексные числа,

• а a₁,a₂,...,a_k–натуральные числа, причем:

• a₁+ a₂+ ... + a_k= n

• Отсюда следует,что числа Z₁,Z₂,...,Z_Kявляются корнями уравнения

Понятие корня степени n

Корнем степени n из действительного числа a, где n - натуральное число, называется такое действительное число x, n-ая степень которого равна a.

Корень степени n из числа a обозначается символом  . Согласно этому определению  .

Нахождение корня n-ой степени из числа a называется извлечением корня. Число аназывается подкоренным числом (выражением), n - показателем корня. При нечетномn существует корень n-ой степени для любого действительного числа a. При четномn существует корень n-ой степени только для неотрицательного числа a. Чтобы устранить двузначность корня n-ой степени из числа a, вводится понятие арифметического корня n-ой степени из числа a.