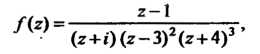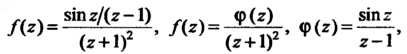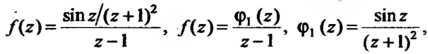- •Рациональное число как десятичная дробь
- •Периодическая дробь
- •Приближенные значения числа . Свойство абсолютной величины суммы
- •1.Понятие комплексного числа
- •2.Геометрическая интерпретация
- •3.Модуль комплексного числа
- •4.Сложение и умножение комплексных чисел
- •5.Вычитание и деление комплексных чисел
- •6.Тригонометрическая форма
- •7.Свойства модуля и аргумента
- •8.Возведение в степень и извлечение корня
- •Понятие корня степени n
- •Понятие арифметического корня степени n
- •Поятие степени с рациональным показателем
- •Степень с действительным показателем
- •Решение простейших показательных уравнений.
- •Решение простых показательных уравнений. Примеры.
- •Замена переменной в решении показательных уравнений. Примеры.
- •Показательные неравенства: примеры и достаточные знания, необходимые для решения заданий
- •Логарифмы
- •Основные свойства логарифмов
- •Сложение и вычитание логарифмов
- •Вынесение показателя степени из логарифма
- •Переход к новому основанию
- •Основное логарифмическое тождество
- •Логарифмическая единица и логарифмический ноль
- •Что такое логарифмическое уравнение?
- •Как решать логарифмические уравнения?
- •Логарифмические неравенства Определение
- •Переход к новому основанию логарифма
- •§ 53. Переход к новому основанию логарифма
- •Функция синус
- •Функция косинус
- •Функция тангенс
- •Функция котангенс
- •Знаки тригонометрических функций
- •Тема 16. "Простейшие тригонометрические неравенства".
- •Основные понятия и свойства функций
- •Экстремумы функции
Основные понятия и свойства функций
Ключевые слова: область определения функции, область значений функции четная функция, нечетная функция, периодическая функция. монотонная функция. убывающая функция. возрастающая функция, ограниченная функция.
В элементарной математике изучаются функции только на множестве действительных чисел R. Это значит, что аргумент функции может принимать только те действительные значения, при которых функция определена, т.e.она также принимает только действительные значения.
Множество X всех допустимых действительных значений аргументаx, при которых функция y = f (x) определена, называется областью определения функции. Множество Y всех действительных значений y, которые принимает функция,называется областью значений функции.
Теперь можно дать более точное определение функции:
правило(закон) соответствия между множествами X и Y, по которому для каждого элемента из множества X можно найти один и только один элемент из множества Y, называется функцией.
|
|
Функция считается заданной, если:
задана область определения функции X ;
задана область значений функции Y ;
известно правило (закон) соответствия, причем такое, что для каждого значения аргумента может быть найдено только одно значение функции. Это требование однозначности функции является обязательным.
Если для любых двух значений аргумента x1и x2 из условия x2 > x1 следует f ( x2 ) > f ( x1 ), то функция f (x ) называется возрастающей; если для любых x1 и x2 из условия x2 > x1 следует f (x2)< f (x1),то функция f (x ) называется убывающей. Функция, которая только возрастает или только убывает, называется монотонной.
Функция
называется ограниченной,
если существует такое положительное
число M,
что |f
( x )|![]() M для
всех значений x .
Если
такого числа не существует, то функция
- неограниченная.
M для
всех значений x .
Если
такого числа не существует, то функция
- неограниченная.

Функция y = f (x) называется непрерывной в точке x = a, если :
функция определена при x = a, т.e. f (a) существует;
существует конечный предел limx
 af(x);
af(x);f (a) = limx af(x) .
Если не выполняется хотя бы одно из этих условий, то функция называется разрывной в точке x = a. Если функция непрерывна во всех точках своей области определения, то она называется непрерывной функцией.
Если для любого x из области определения функции имеет место: f ( - x ) = f ( x ), то функция называется чётной; если же имеет место: f (-x) = - f (x), то функция называется нечётной.
График чётной функции симетричен относительно оси Y ( рис.5 ), a график нечётной функции симметричен относительно начала координат ( рис.6 ).

Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f ( x + T ) = f ( x ). Такое наименьшее число называется периодом функции.
Все тригонометрические функции являются периодическими.
Пример
1. Доказать, что sin x имеет период
2![]() .
Решение.
Мы знаем, что sin ( x+ 2
n
) = sin x, где n = 0, ± 1, ± 2, …
Следовательно,
добавление 2
n
к аргументу синуса не меняет его
значениe.
Предположим,
что P – такое число, т.e. равенство: sin (
x+ P ) = sin x, справедливо для любогозначения
x.
Но
тогда оно имеет место и при x =
/
2 , т.e. sin (
/
2 + P ) = sin
/
2 = 1.
Но
по формуле приведения sin (
/
2 + P ) = cos P.
Тогда
из двух последних равенств следует,
чтоcos P = 1, но мы знаем, что это верно лишь
при P = 2
n.
Так
как наименьшим отличным от нуля числом
из 2
n
является 2
,
то это число и есть период sin x.
Рассмотрим
sin 2x = sin ( 2x + 2
n
) = sin [ 2 ( x +
n
) ] .
Мы
видим,что добавление
n
к аргументу x, не меняет значение
функции.
Наименьшее
отличное от нуля число из
n
есть
,
таким образом, это период sin 2x .
.
Решение.
Мы знаем, что sin ( x+ 2
n
) = sin x, где n = 0, ± 1, ± 2, …
Следовательно,
добавление 2
n
к аргументу синуса не меняет его
значениe.
Предположим,
что P – такое число, т.e. равенство: sin (
x+ P ) = sin x, справедливо для любогозначения
x.
Но
тогда оно имеет место и при x =
/
2 , т.e. sin (
/
2 + P ) = sin
/
2 = 1.
Но
по формуле приведения sin (
/
2 + P ) = cos P.
Тогда
из двух последних равенств следует,
чтоcos P = 1, но мы знаем, что это верно лишь
при P = 2
n.
Так
как наименьшим отличным от нуля числом
из 2
n
является 2
,
то это число и есть период sin x.
Рассмотрим
sin 2x = sin ( 2x + 2
n
) = sin [ 2 ( x +
n
) ] .
Мы
видим,что добавление
n
к аргументу x, не меняет значение
функции.
Наименьшее
отличное от нуля число из
n
есть
,
таким образом, это период sin 2x .
Значение аргумента, при котором функция равна 0, называется нулём (корнем) функции.
Функция может иметь несколько нулей.
Например, функция y = x (x + 1)(x-3) имеет три нуля: x = 0, x = - 1, x =3.
Геометрически нуль функции – это абсцисса точки пересечения графика функции с осью Х .
На рис.7 представлен график функции с нулями: x = a, x = b и x = c .

Нули функции. Особые точки |
|
|
|
Нули
функции. Рассмотрим функцию
Если Значение
Где Особые
точки. Особой точкой функции Для
того, чтобы точка
Точку Точка
является нулем порядка Полюс называют простым. Для
того, чтобы точка
Где Точка Функция Справедливы следующие утверждения. 1.
Точка 2.
Точка
Наибольший
из показателей степени разности Совпадает с порядком полюса. 3.
Точка Пример
37.31. Доказать, что точка Рядка
для функции Разложим
в ряды данную функцию и ее первую и
вторую производные: Поскольку При Пример
37.32. Найти порядок нуля Использовав
разложение функции
Таким
образом, функция _ Четвертого порядка для данной функции. Пример
37.33. Найти нули функции Когда Равенства
следует, что Пусть
Точке Третьего
порядка. Аналогично доказывается,
что
Это
нули первого порядка для функции
Пример
37.34. Доказать, что точка
Действительно,
поскольку
Пример
37.35. Найти полюсы функции Так
как для функции Нули
первого порядка,
Замечание.
Если Не
имеющие общих корней, то корни
многочлена Ветствующих
корней многочлена
То
Поскольку То
функция имеет особые точки
Где
Заключаем,
что Пример
37.37. Найти особые точки функции Лить их типы. Принимая во внимание, что (см. (37.3))
При
Этот
ряд сходится всюду, кроме точки Разложение
функции Главная
часть ряда имеет бесконечное множество
членов, то точка |



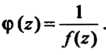 (37.49)
(37.49)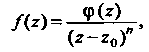 (37.50)
(37.50)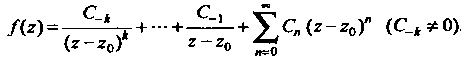 (37.51)
(37.51)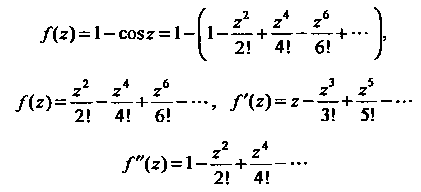
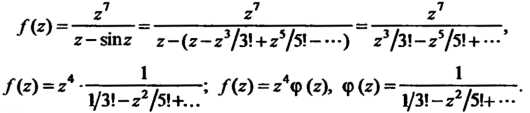
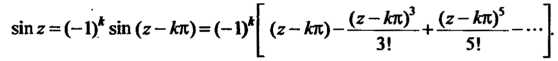

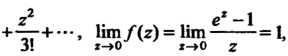 То
То