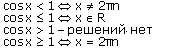Знаки тригонометрических функций
Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент. В прошлый раз мы учились переводить аргументы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а затем определять эту самую координатную четверть. Теперь займемся, собственно, определением знака синуса, косинуса и тангенса.
Определение
Синус угла α — это ордината (координата y) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
Определение
Косинус угла α — это абсцисса (координата x) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.
Определение
Тангенс угла α — это отношение синуса к косинусу. Или, что то же самое, отношениекоординаты y к координате x.
Обозначение
sin α = y; cos α = x; tg α = y : x.
Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните:
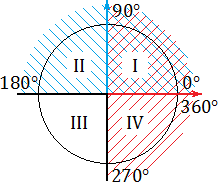
Синим цветом обозначено положительное направление оси OY (ось ординат), красным — положительное направление оси OX (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:
sin α > 0, если угол α лежит в I или II координатной четверти. Это происходитиз-за того, что по определению синус — это абсцисса (координата y). А координата yбудет положительной именно в I и II координатных четвертях;
cos α > 0, если угол α лежит в I или IV координатной четверти. Потому что только тамкоордината x (она же — абсцисса) будет больше нуля;
tg α > 0, если угол α лежит в I или III координатной четверти. Это следует из определения: ведь tg α = y : x, поэтому он положителен лишь там, где знаки x и yсовпадают. Это происходит в I координатной четверти (здесь x > 0, y > 0) и III координатной четверти (x < 0, y < 0).
Для наглядности отметим знаки каждой тригонометрической функции — синуса, косинуса и тангенса — на отдельных «радарах». Получим следующую картинку:
Заметьте: в своих рассуждениях я ни разу не говорил о четвертой тригонометрической функции — котангенсе. Дело в том, что знаки котангенса совпадают со знаками тангенса — никаких специальных правил там нет.
Теперь предлагаю рассмотреть примеры, похожие на задачи B7 из пробного ЕГЭ по математике, который проходил 27 сентября 2011. Ведь лучший способ понять теорию — это практика. Желательно — много практики. Разумеется, условия задач были немного изменены.
Тема 16. "Простейшие тригонометрические неравенства".
Проверь себя: тесты по английскому языку на ШКола.lv!
Неравенства
: sin x > a, sin x 
a,
sin x < a, sin x 
a
Sin
x > a 
arcsin
a + 2 
n
< x <
–
arcsin a + 2
n,
n 
Z
=
arcsin a; 
=
–
arcsin a.
sin x<a – – arcsin a + 2 n<x< arcsin a + 2 n, n Z
= – – arcsin a ; = arcsin a.
В случае нестрогих неравенств знаки < и > в решениях заменяются соответственно на и .
|
|
|
|
|
|
|
|
Во всех приведенных здесь формулах n Z.
Неравенства:
cos x> a; cos x a; cos x < a; cos x a.
В случае нестрогих неравенств знаки < и > в решениях заменяются соответственно на и .
|
|
|
|
|
|
|
|
Во всех приведенных здесь формулах n Z.
Неравенства:
tg x > a; tg x a; tg x < a; tg x a.
Рекомендации к теме теория >>
Решение неравенств, содержащих тригонометрические функции, сводится, как правило, к решению простейших неравенств вида sin t > a, cos t a, tg t a и т.п.
Простейшие тригонометрические уравнения решаются при помощи единичной окружности или графика соответствующей тригонометрической функции.
Следует обратить внимание на область определения функций у= tg t : решения нестрогих неравенств не всегда получаются из решений соответствующих строгих неравен ств пр осто заменой знаков > и < на знаки и .
Рассмотрим на примерах способы решений тригонометрических неравенств.
Примеры.
1.Решить неравенство cos x 1/2.
Решение: Абсциссу, не большую 1/2, имеют все точки дуги М1ММ2 единичной окружности (см. рисунок).
Поэтому решениями неравенства cos x 1/2 являются числа х, принадлежащие промежутку /3 х 5 /3. Все решения данного неравенства – множество отрезков [ /3 +2 n ; 5 /3+2 n ], n Z.
Ответ: [ /3 +2 n ; 5 /3+2 n ], n Z.
2.Решить неравенство tg x > 1.
Решение: Построим графики функций у = tg x и у = 1.
Рисунок показывает, что график функции у = tg x лежит выше прямой у=1 на промежутке ( /4; /2), а также на промежутках, полученных сдвигами его на n, где n Z.
Ответ: ( /4+ n ; /2 + n ), где n Z.