1 билет

Действительные числа

Число, которое можно записать в виде отношения

, где m - целое число, а n - натуральное число,

називают рациональным числом.

Любое рациональное число можно представить в виде конечной дроби или бесконечной периодической десятичной дроби.

Например,

Бесконечная десятичная дробь, это десятичная дробь, в записи которой после запятой содержится бесконечное количество цифр.

Числа, которые нельзя представить в виде

, называют иррациональными числами.

Это, например, числа

Любое иррациональное число можно представить в виде бесконечной непериодической десятичной дроби.

Например,

Рациональные числа и иррациональные числа образуют множество действительных чисел . Каждому действительному числу соответствует единственная точка координатной прямой. которую называют числовой прямой . Для числовых множеств используются обозначения:  N - множество натуральных чисел;  Z - множество целых чисел;  Q - множество рациональных чисел;  R - множество действительных чисел. 

Рациональное число как десятичная дробь

Любое рациональное число является значением некоторой конечной или бесконечной периодической дроби. Наоборот, значение любой конечной или бесконечной периодической дроби — рациональное число.

Замечание. Если исключить из рассмотрения дроби с периодом (9), то каждое рациональное число представляется единственной десятичной дробью.

Примеры.  ;  ;   и т.п.

Периодическая дробь

Периодическая дробь

        бесконечная десятичная дробь, в которой, начиная с некоторого места, стоит только периодически повторяющаяся определённая группа цифр. Например, 1,3181818...; короче эту дробь записывают так: 1,3(18), то есть помещают период в скобки (и говорят: «18 в периоде»). П. д. называется чистой, если период начинается сразу после запятой, например 2(71) = 2,7171..., и смешанной, если после запятой имеются цифры, предшествующие периоду, например 1,3(18). Роль П. д. в арифметике обусловлена тем, что при представлении рациональных чисел, то есть обыкновенных (простых) дробей, десятичными дробями, всегда получаются либо конечные, либо периодические дроби. Точнее: конечная десятичная дробь получается в том случае, когда знаменатель несократимой простой дроби не содержит других простых множителей, кроме 2 и 5; во всех других случаях получается П. д., и притом чистая, если знаменатель данной несократимой дроби вовсе не содержит множителей 2 и 5, и смешанная, если хотя бы один из этих множителей содержится в знаменателе. Всякая П. д. может быть обращена в простую дробь (то есть она равна некоторому рациональному числу). Чистая П. д. равна простой дроби, числителем которой служит период, а знаменатель изображается цифрой 9, написанной столько раз, сколько цифр в периоде; при обращении в простую дробь смешанной П. д. числителем служит разность между числом, изображаемым цифрами, предшествующими второму периоду, и числом, изображаемым цифрами, предшествующими первому периоду; для составления знаменателя надо написать цифру 9 столько раз, сколько цифр в периоде, и приписать справа столько нулей, сколько цифр до периода. Эти правила предполагают, что данная П. д. правильная, то есть не содержит целых единиц; в противном случае целая часть учитывается особо.

         Примеры:

        

         

         Известны также правила определения длины периода П. д., соответствующей данной обыкновенной дроби. Например, для дроби a/p, где р — простое число и 1 ≤ a ≤ p —1, длина периода является делителем р — 1. Так, для известных приближений к числу (см. Пи) ²²/₇ и ³⁵⁵/₁₁₃ период равен 6 и 112 соответственно.

Приближенные значения числа . Свойство абсолютной величины суммы

На практике мы почти никогда не знаем точных значений величин. Никакие весы, как бы точны они ни были, не показывают вес абсолютно точно; любой термометр показывает температуру с той или иной ошибкой; никакой амперметр не может дать точных показаний тока и т. д. К тому же наш глаз не в состоянии абсолютно правильно прочитать показания измерительных приборов. Поэтому, вместо того  чтобы иметь дело с истинными значениями величин, мы вынуждены оперировать с их  приближенными  значениями.

Тот факт, что а' есть приближенное значение числа а, записывается  следующим  образом:

а ≈ а'.

Если а' есть приближенное значение величины а, то разность Δ = а — а'   называетсяпогрешностью приближения*.

*  Δ — греческая   буква;   читается:   дельта. Далее встречается еще одна греческая буква ε (читается:   эпсилон).

Например, если число 3,756 заменить его приближенным значением 3,7, то погрешность будет равна: Δ = 3,756 — 3,7 = 0,056. Если в качестве приближенного значения взять 3,8, то погрешность будет равна:  Δ = 3,756 — 3,8 = —0,044.

На практике чаще всего пользуются не погрешностью приближения Δ, а абсолютной величиной этой погрешности |Δ|. В дальнейшем эту абсолютную величину погрешности мы будем называть просто абсолютной погрешностью. Считают, что одно приближение лучше другого, если абсолютная погрешность первого приближения меньше абсолютной погрешности второго приближения. Например, приближение 3,8 для числа 3,756 лучше, чем приближение 3,7, поскольку для первого приближения |Δ| = | — 0,044| =0,044, а для второго |Δ| = |0,056| = 0,056.

Число а' называется приближенным значением числа а с точностью до ε, если абсолютная погрешность этого приближения меньше чем ε:

|а — а'|  <  ε.

Например, 3,6 есть приближенное значение числа 3,671 с точностью до 0,1, поскольку  |3,671 — 3,6| = | 0,071| = 0,071< 0,1.

Аналогично, — ³/₂ можно рассматривать как   приближенное значение числа  — ⁸/₅  с точностью до  ¹/₅ , поскольку

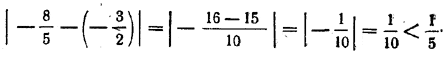
Если а' < а, то а' называется приближенным значением числа а с недостатком.

Если же а' > а, то а' называется приближенным значением числа а с избытком.

Например, 3,6 есть приближенное значение   числа 3,671   с недостатком,   поскольку 3,6 < 3,671,   а — ³/₂ есть   приближенное   значение   числа — ⁸/₅ c избытком, так как — ³/₂ > — ⁸/_{5 .}

Если мы вместо чисел а и b сложим их приближенные значения а' и b', то результат   а' + b'  будет приближенным значением суммы а + b. Возникает вопрос: как оценить точность этого результата, если известна точность приближения каждого слагаемого? Решение этой и подобных ей задач основано на следующем свойстве абсолютной величины:

|а + b|  <  |a| + |b|.

Абсолютная величина суммы любых двух чисел не превышает суммы их абсолютных величин.

Доказательство. Если числа а и b положительны, то и сумма их положительна. В этом случае |а| = а, |b| = b, |а+ b| = а + b и, следовательно, |а+ b| = |a| + |b|.

Если числа а и b отрицательны, то и сумма их отрицательна. В этом случае |а| = — а, |b| = — b, |а + b| = — (а + b); поэтому |а + b| также равняется |а| + |b|.

Пусть, наконец, одно из чисел а и b положительно, а другое— отрицательно. Тогда если |а|>|b|, то |а + b| = |а| — | b|; если же | а| < | b |, то |a + b|= |b| — |a|.

В любом из этих случаев разность двух положительных чисел |а| и |b| будет меньше их суммы. Таким образом, если одно из чисел а и b положительно,   а другое отрицательно,   то

|а + b|  <  |a| + |b|.

Осталось  рассмотреть лишь  случай,   когда    одно из    чисел а и b, а может быть, и оба равны нулю. Учащиеся   без особого труда  могут сделать  это самостоятельно.

Пример.    | 1 — 20 | < | 1 | + | —20|.

Действительно,

|1 — 20| = |—19| = 19,

|1| + | — 20| = 1 + 20 = 21,

19 < 21.

Округление

В разных сферах могут применяться различные методы округления. Во всех этих методах «лишние» знаки обнуляют (отбрасывают), а предшествующий им знак корректируется по какому-либо правилу.

• Округление к ближайшему целому (англ. rounding) — наиболее часто используемое округление, при котором число округляется до целого, модуль разности с которым у этого числа минимален. В общем случае, когда число в десятичной системе округляют до N-ого знака, правило может быть сформулировано следующим образом:

  • если N+1 знак < 5, то N-ый знак сохраняют, а N+1 и все последующие обнуляют;

  • если N+1 знак ≥ 5, то N-ый знак увеличивают на единицу, а N+1 и все последующие обнуляют;

Например: 11,9 → 12; −0,9 → −1; −1,1 → −1; 2,5 → 3.