76Сложность алгоритмов. Меры сложности алгоритмов. Сложность задачи. Массовые и индивидуальные задачи.

Вычислительная сложность алгоритма — это функция, определяющая зависимость объёма работы, выполняемой некоторым алгоритмом, от размера входных данных.

В рамках классической теории осуществляется классификация задач по классам сложности (P-сложные, NP-сложные, экспоненциально сложные и др.). К классу P относятся задачи, которые могут быть решены за время, полиномиально зависящее от объёма исходных данных, с помощью детерминированной вычислительной машины (например, машины Тьюринга), а к классу NP — задачи, которые могут быть решены за полиномиально выраженное время с помощью недетерминированной вычислительной машины, то есть машины, следующее состояние которой не всегда однозначно определяется предыдущими. Работу такой машины можно представить как разветвляющийся на каждой неоднозначности процесс: задача считается решённой, если хотя бы одна ветвь процесса пришла к ответу. Другое определение класса NP: к классу NP относятся задачи, решение которых с помощью дополнительной информации полиномиальной длины, данной нам свыше, мы можем проверить за полиномиальное время. В частности, к классу NP относятся все задачи, решение которых можно проверить за полиномиальное время. Класс P содержится в классе NP.

Пусть:А – алгоритм решения некоторого класса задач и n-размерность одной задачи из этого клаcса

функция fA(n) даст верхнюю границу для максимального числа основных операций, которые должен выполнить алгоритм А для решения любой задачи размерности n.

Тогда алгоритм называется полиномиальным, если fA(n) растет не быстрее чем полином от n. В противном случае алгоритм А называется экспоненциальным. Так, функции типа kn, kn2,kn3,..., где k – коэфициент, могут рассматриваться как полиномиальные, а функции типа 2n, nn, n!... как экспоненциальнные.

Массовая задача определяется: • списком параметров – свободных переменных, конкретные значения которых неопределенны; • формулировкой условий – свойств, которыми должен обладать ответ.

Инидивидуальная задача получается из массовой, если всем параметрам массовой задачи придать конкретные значения – здесь исходные данные.

77Асимптотическая сложность, порядок сложности. Сложность в среднем и в худшем случае.

Рассмотрение входных данных большого размера и оценка порядка роста времени работы алгоритма приводят к понятию асимптотической сложности алгоритма. Для записи асимптотической сложности алгоритмов используются асимптотические обозначения:

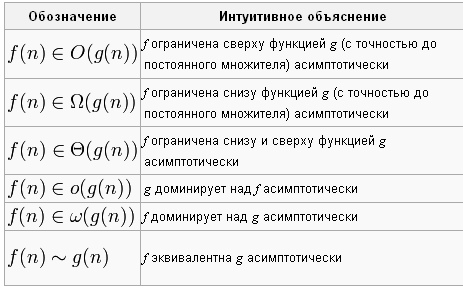
«пропылесосить ковер» требует время, линейно зависящее от его площади (Θ(A)), то есть на ковер, площадь которого больше в два раза, уйдет в два раза больше времени. Соответственно, при увеличении площади ковра в сто тысяч раз, объем работы увеличивается строго пропорционально в сто тысяч раз.

А) Худший случай

Максимальное количество переприсваиваний максимума (на каждом проходе цикла) будет в том случае, если элементы массива отсортированы по возрастанию. Трудоемкость алгоритма в этом случае равна:

F_A^(n)=1+1+1+ (n-1) (3+2+2)=7 n - 4 = Q(n).

Б) Лучший случай

Минимальное количество переприсваивания максимума (ни одного на каждом проходе цикла) будет в том случае, если максимальный элемент расположен на первом месте в массиве. Трудоемкость алгоритма в этом случае равна:

F_A^Ú(n)=1+1+1+ (n-1) (3+2)=5 n - 2 = Q(n).

78Трудоемкость алгоритмов. Классификация алгоритмов по виду функции трудоёмкости

Трудоемкость алгоритма это количество элементарных операций, которые необходимо выполнить для решения задачи с помощью данного алгоритма

Для получения функции трудоемкости алгоритма, представленного в формальной системе введенной абстрактной машины необходимо уточнить понятия «элементарных» операций. В качестве таких «элементарных» операций предлагается использовать следующие:

1. Простое присваивание: а ¬ b;

2. Одномерная индексация a[i] : (адрес (a)+i* длина элемента);

3. Арифметические операции: (*, /, -, +);

4. Операции сравнения: a < b;

5. Логические операции (l₁) {or, and, not} (l₂);

Конструкция «Следование»

Трудоемкость конструкции есть сумма трудоемкостей блоков, следующих друг за другом.

F _{«следование»} = f₁ + … + f_k, где k – количество блоков.

Конструкция «Ветвление»

if ( l ) then f_then с вероятностью p

else f_else с вероятностью (1 - p)

Общая трудоемкость конструкции «Ветвление» требует анализа вероятности выполнения переходов на блоки «Then» и «Else» и определяется как: F _{«ветвление»} = f_then * p + f_else * (1-p).

Конструкция «Цикл»

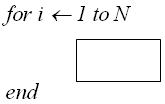
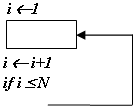F_«цикл» = 1+3*N+N*f_{«тела цикла»}

79Методики перехода к временным оценкам трудоёмкости алгоритмов. Пооперационный анализ. Метод Гиббсона. Метод прямого определения среднего времени.

Дано: F_A(D_A) – трудоёмкость алгоритма. Требуется определить время работы программной реализации алгоритма – T_A(D_A).

1) Пооперационный анализ

• Получить пооперационную функцию трудоемкости для каждой из используемых алгоритмом элементарных операций с учетом типов данных.

• Экспериментальное определение среднего времени выполнения данной элементарной операции на конкретной вычислительной машине.

• Ожидаемое время выполнения рассчитывается как сумма произведений пооперационной трудоемкости на средние времена операций: T_A(N) = å F_{А оп i}(N) * `t _{оп i}

2) Метод Гиббсона

Метод предполагает проведение совокупного анализа по трудоемкости и переход к временным оценкам на основе принадлежности решаемой задачи к одному из следующих типов:

• задачи научно-технического характера с преобладанием операций с операндами действительного типа;

• задачи дискретной математики с преобладанием операций с операндами целого типа;

• задачи баз данных с преобладанием операций с операндами строкового типа;

Далее на основе анализа множества реальных программ для решения соответствующих типов задач определяется частотная встречаемость операций, создаются соответствующие тестовые программы, и определяется среднее время на операцию в данном типе задач –`t _{тип задачи}.