72Нормальные алгорифмы Маркова. Нормально вычислимые функции и принцип нормализации Маркова.

Нормальные алгорифмы Маркова это один из стандартных способов формального определения понятия алгоритма. Нормальный алгоритм описывает метод переписывания строк, похожий по способу задания на формальные грамматики. Нормальные алгоритмы являются вербальными, то есть предназначенными для применения к словам в различных алфавитах. Определение всякого нормального алгоритма состоит из двух частей: определения алфавита алгоритма (к словам из символов которого алгоритм будет применяться) и определения его схемы. Схемой нормального алгоритма называется конечный упорядоченный набор т. н. формул подстановки, каждая из которых может быть простой или заключительной. Простыми формулами подстановки называются слова вида , где L и D — два произвольных слова в алфавите алгоритма (называемые, соответственно, левой и правой частями формулы подстановки).

Нормальный алгоритм Маркова можно рассматривать как универсальную форму задания любого алгоритма. Универсальность нормальных алгоритмов декларируется принципом нормализации (тезис Маркова): для любого алгоритма в произвольном конечном алфавите А можно построить эквивалентный ему нормальный алгоритм над алфавитом А. Другими словами, всякий алгоритм нормализуем.

Функция f, заданная на некотором множестве слов алфавита А, называется нормально вычислимой, если найдется такое расширение B данного алфавита (А с_ В) и такой нормальный алгоритм в В, что каждое слово V (в алфавите А) из области определения функции f этот алгоритм перерабатывает в слово f(V).

73Вычислимость и разрешимость. Нумерация алгоритмов. Алгоритмически разрешимые и неразрешимые задачи. Проблема остановки, проблема самоприменимости, проблема пустой ленты.

Машина Тьюринга Т задает словарную функцию над некоторым алфавитом V и представляет собой описание машины — набор (F, Q, q0, #, I) - и правило функционирования, общее для всех машин, где

V — алфавит машины;

Q — конечное непустое множество символов, называемых состояниями машины (Q V = Æ);

q0 — выделенный элемент множества Q, называемый начальным состоянием;

# — специальный «пустой» символ, не принадлежащий ни V, ни Q;

I — программа машины.

Программа машины — это конечное множество слов вида qa q'a'd, называемых командами, где q, q' Q, a, a' V {#}; — вспомогательный символ-разделитель; d — элемент множества {l, r, р}, содержащего три специальных символа, которых нет ни в V, ни в Q. Предполагается также, что в программе I никакие две команды не могут иметь одинаковую пару первых двух символов.

По определению, функция F является вычислимой, если существует машина Тьюринга Т такая, что FT = F(где FT это частичная функция). Говорят также, что для функции F существует (частичный) алгоритм вычисления ее значений, задаваемый машиной Т.

Множество М называется разрешимым, если его характеристическая функция вычислима.

Пусть V – алфавит, М V – множество слов в V.

Характеристической функцией множества М называется предикат FM: V* {0, 1}, всюду определенный на V*: FM(а) = 1, если а принадлежит М, и FM(а) = 0, если а не принадлежит М.

Проблема остановки формулируется так. Пусть М – множество всех пар слов в алфавите V, в каждой паре первое слово – словарное представление некоторой машины Тьюринга, второе – такое слово, что эта машина останавливается, начав работу над ним. Является ли множество М неразрешимым.(ИЛИ:Даны описание алгоритма и его начальные входные данные, требуется определить, сможет ли выполнение алгоритма с этими данными завершиться когда-либо.) Самопримени́мость — свойство алгоритма успешно завершаться на данных, представляющих собой формальную запись этого же алгоритма.Задача распознавания самоприменимости является алгоритмически неразрешимой и сводится к тому, чтобы найти алгоритм, позволяющий за конечное число шагов по формальной записи некоего алгоритма узнать, является ли он самоприменимым или нет. Не существует алгоритма, который по любой МТ определял бы остановится эта машина стартуя с пустой ленты или нет.

Допустим, что есть алгоритм Р, решающий по любой М, остановится она или нет, стартуя с пустой ленты.Построим на его основании алгоритм, решающий по любому х, определено К(х,х) или нет.

Вход: х

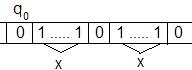
Пусть Мх – машина, которая, стартуя с пустой ленты, печатает

Построим композицию машины Мх и , и обозначим

Для запускаем алгоритм Р и определяем, остановится она или нет, стартуя с пустой ленты. Ясно теперь, что К(х,х) определено <=> Р дает положительный ответ. Противоречие.

74Требование результативности и теория алгоритмов.

Требование результативности–вычислительный процесс обязательно должен выполняться за конечное число шагов и завершаться получением результата решения задачи. Тео́рия алгори́тмов — наука, изучающая общие свойства и закономерности алгоритмов и разнообразные формальные модели их представления.

75Разрешимые и перечислимые множества. Связь между разрешимостью и перечислимостью множеств. Теорема Райса.

Разрешимым называется множество целых чисел для которого существует алгоритм определения принадлежности ему некоторого элемента. Для разрешимого множества А задаётся вычислимая и всюду определённая функция :

Перечислимым называется подмножество натуральных чисел, все элементы которого можно получать (перечислять) при помощи алгоритма. Это означает что существует некоторая функция, которая в своей памяти последовательно размещает числа.

Любое разрешимое множество перечислимо, но перечислимое множество не обязательно разрешимо

Вычислимая функция – это функция, которая вычисляется каким-либо алгоритмом.

Термин «вычисляется» означает следующее:если на вход алгоритма подано значение аргумента из области определения функции, то на выходе получается результат, совпадающий со значением функции на этом входе;

Теорема Райса:Пусть Q - некоторое свойство одноместных интуитивно вычислимых функций. Назовем свойство Q нетривиальным , если в множестве A существуют и функции, обладающие этим свойством, и функции, не обладающие им. Тогда теорему Райса можно переформулировать так:

Каково бы не было нетривиальное свойство Q одноместных интуитивно вычислимых функций, задача распознавания этого свойства алгоритмически неразрешима.