
- •Исследование; цели, типовые задачи, общенаучные методы исследования.
- •3.Графическая формализация.
- •4. Структурная формализация.
- •Если важно отразить упорядоченность элементов, то надо использовать не множество, а кортеж:
- •5. Структурно-параметрическая формализация.
- •6. Параметрическая формализация. Классификация параметрических моделей.
- •7. Выбор факторов и характеристик, учитываемых в модели. Модели экстраполяции, «вход-выход» и общая модель динамики.
- •8.Кусочно-линейная интерполяция и экстраполяция
- •9.Квадратичная интерполяция и экстраполяция
- •10. Линейная аппроксимация. Метод наименьших квадратов.
- •11.Классификация моделей по временному промежутку, для которого осуществляется моделирование. Модели жизненного цикла и эволюции.
- •12.Конечные разности первого и второго порядка.
- •13.Рекуррентные последовательности и их задание с помощью конечных разностей.
- •14. Разностные уравнения и их виды. Решение разностного уравнения.
- •Решение разностного уравнения:
- •15. Линейные возвратные уравнения. Вид решения однородного и неоднородного возвратного уравнения.
- •16.Линейные возвратные уравнения первого порядка. Уравнения для арифметической и геометрической прогрессий.
- •17. Линейные возвратные уравнения второго порядка с постоянными коэффициентами. Характеристическое уравнение и его значение для нахождения решения.
- •18. Линейные возвратные уравнения второго порядка с постоянными коэффициентами. Вид решения при действительных корнях характеристического уравнения.
- •19. Линейные возвратные уравнения второго порядка с постоянными коэффициентами. Вид решения при комплексных корнях характеристического уравнения.
- •20. Собственные числа и собственные векторы квадратных матриц. Их свойства.
- •21. Системы линейных возвратных уравнений первого порядка с постоянными коэффициентами. Их решение для случая двух уравнений с двумя переменными.
- •22. Устойчивость системы разностных уравнений.
- •23.Импульсные (когнитивные) модели. Их назначение и параметризация.
- •24. Импульсный процесс и правила его развития. Уравнения импульсного процесса.
- •Уравнение импульсного процесса
- •25. Решение уравнений импульсного процесса. Виды устойчивости импульсного процесса.
- •26. Основные понятия дифференциальных уравнений.
- •29. Линейные дифференциальные уравнения первого порядка.
- •30.Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Характеристическое уравнение и его значение для нахождения решения.
- •33) Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •34. Системы линейных однородных дифференциальных уравнений первого порядка с постоянными коэффициентами. Вид решения.
- •35.Неоклассические производственные функции.
- •36. Мультипликативная производственная функция задается выражением
- •37.Эластичность производственной функции. Модель роста выпуска.
- •38.Динамическая модель Кейнса
- •45.Динамическая модель Леонтьева. Условия и уравнения.
- •46.Распределения случайных величин: Бернулли и Пуассона.
- •47.Распределения случайных величин: экспоненциальное и нормальное.
- •49.Теорема Чебышева. Закон больших чисел.
- •50.Центральная предельная (теорема Ляпунова)
- •51. Теорема (интегральная формула) Муавра-Лапласа.
- •52. Понятие о статистической оценке параметров. Числовые характеристики выборочного распределения.
- •53. Точечные оценки и их характеристики. Выборочные среднее и дисперсия.
- •54. Понятие об интервальной оценке параметров. Доверительная вероятность и доверительный интервал.
- •55. Интервальная оценка для математического ожидания.
- •56. Случайные процессы. Основные понятия и характеристики.
- •57. Марковские процессы. Конечные цепи Маркова.
- •Отличие Марковского процесса от Марковской цепи
- •58. Потоки событий. Простейший поток.
33) Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Линейное неоднородное
дифференциальное уравнение (ЛНДУ)
второго порядка с постоянными
коэффициентами имеет вид
![]() ,
где p
и q
– произвольные действительные числа,
а функция f(x)
– непрерывна на интервале интегрирования
X.
*Сформулируем
теорему, которая показывает, в каком
виде искать общее решение ЛНДУ.
*Общее
решение на интервале X
линейного неоднородного дифференциального
уравнения
,
где p
и q
– произвольные действительные числа,
а функция f(x)
– непрерывна на интервале интегрирования
X.
*Сформулируем
теорему, которая показывает, в каком
виде искать общее решение ЛНДУ.
*Общее
решение на интервале X
линейного неоднородного дифференциального
уравнения
![]() с
непрерывными на интервале интегрирования
X
коэффициентами
с
непрерывными на интервале интегрирования
X
коэффициентами
![]() и
непрерывной функцией f(x)
равно сумме общего решения
и
непрерывной функцией f(x)
равно сумме общего решения
![]() соответствующего
ЛОДУ и какого-нибудь частного решения
соответствующего
ЛОДУ и какого-нибудь частного решения
![]() исходного
неоднородного уравнения. То есть,
исходного
неоднородного уравнения. То есть,
![]() .
Таким
образом, общим решением линейного
неоднородного дифференциального
уравнения второго порядка с постоянными
коэффициентами является сумма
.
Нахождение
описано
в статье линейные
однородные дифференциальные уравн.
второго порядка с постоянными
коэффициентами и нам осталось научиться
определять
.
*Существует
несколько методов нахождения частного
решения ЛНДУ второго порядка с постоянными
коэффициентами. Методы выбираются в
зависимости от вида функции f(x),
стоящей с правой части уравнения.
Перечислим их.
.
Таким
образом, общим решением линейного
неоднородного дифференциального
уравнения второго порядка с постоянными
коэффициентами является сумма
.
Нахождение
описано
в статье линейные
однородные дифференциальные уравн.
второго порядка с постоянными
коэффициентами и нам осталось научиться
определять
.
*Существует
несколько методов нахождения частного
решения ЛНДУ второго порядка с постоянными
коэффициентами. Методы выбираются в
зависимости от вида функции f(x),
стоящей с правой части уравнения.
Перечислим их.
Если f(x) является многочленом n-ой степени f(x) = Pn(x), то частное решение ЛНДУ ищется в виде
 ,
где Qn(x)
– многочлен степени n,
а r
– количество корней характеристического
уравнения, равных нулю. Так как
-
частное решение уравнения
,
то коэффициенты, определяющие многочлен
Qn(x),
находятся методом неопределенных
коэффициентов из равенства
,
где Qn(x)
– многочлен степени n,
а r
– количество корней характеристического
уравнения, равных нулю. Так как
-
частное решение уравнения
,
то коэффициенты, определяющие многочлен
Qn(x),
находятся методом неопределенных
коэффициентов из равенства

Если функция f(x) представлена произведением многочлена степени n и экспоненты
 ,
то частное решение ЛНДУ второго порядка
ищется в виде
,
то частное решение ЛНДУ второго порядка
ищется в виде
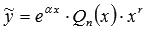 ,
где Qn(x)
– многочлен n-ой
степени, r
– число корней характеристического
уравнения, равных
,
где Qn(x)
– многочлен n-ой
степени, r
– число корней характеристического
уравнения, равных
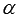 .
Коэффициенты многочлена Qn(x)
определяются из равенства
.
.
Коэффициенты многочлена Qn(x)
определяются из равенства
.
Если функция f(x)
имеет вид
![]() ,
где А1
и В1
– числа, то частное решение ЛНДУ
представляется как
,
где А1
и В1
– числа, то частное решение ЛНДУ
представляется как
![]() ,
где А
и В
– неопределенные коэффициенты, r
– число комплексно сопряженных пар
корней характеристического уравнения
равных
,
где А
и В
– неопределенные коэффициенты, r
– число комплексно сопряженных пар
корней характеристического уравнения
равных
![]() .
Коэффициенты многочлена А
и В
находятся из равенства
.
.
Коэффициенты многочлена А
и В
находятся из равенства
.
34. Системы линейных однородных дифференциальных уравнений первого порядка с постоянными коэффициентами. Вид решения.
Линейные однородные системы диф.уравнений 1-го порядка имеют вид:

 (1)
(1)
Если ввести векторы
 и
и
 ,
то систему (1) можно записать в векторном
виде Z’=A*Z,
где
,
то систему (1) можно записать в векторном
виде Z’=A*Z,
где
 .
Пара функций x(t)
и y(t)
называется решением системы (1), если
она превращает оба ее уравнения, а
следовательно и уравнение (2), в
тождества.Решение:Выпазим у из 1-го
уравнения системы (1):
.
Пара функций x(t)
и y(t)
называется решением системы (1), если
она превращает оба ее уравнения, а
следовательно и уравнение (2), в
тождества.Решение:Выпазим у из 1-го
уравнения системы (1):
 .
Продифференцируем это выражение
.
Продифференцируем это выражение
 и подставим у и у’ во второе уравнение
системы (1)
и подставим у и у’ во второе уравнение
системы (1)
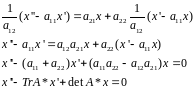
где TrA – след матрицы А, detA – ее определитель
 (3)
Выразив х из 2-го уравнения системы (1)
и, действуя аналогично, получим
(3)
Выразив х из 2-го уравнения системы (1)
и, действуя аналогично, получим
 (4). Имеем однородное дифференциальное
уравнение 2-го порядка с постоянными
коэффициентами. Его характеристическое
уравнение:
(4). Имеем однородное дифференциальное
уравнение 2-го порядка с постоянными
коэффициентами. Его характеристическое
уравнение:
 (5)
(5)
По теореме Виетта корни уравнения обладают свойствами:
 ;
;

Но этими же свойствами обладают и собственные числа матрицы А, которые, следовательно, являются корнями характеристического уравнения.
Общее решение уравнений (3) и (4):
 (6)
(6)
 (7), где вид функций
(7), где вид функций
 и
и
 определяется
типом корней характеристического
уравнения (5). Начальные условия для
уравнений (6) и (7), а следовательно и
неопределенные коэффициенты С1,С2,В1,В2
не являются независимыми. Они связаны
двумя уравнениями системы (1). Поэтому
независимых коэффициентов только два.
определяется
типом корней характеристического
уравнения (5). Начальные условия для
уравнений (6) и (7), а следовательно и
неопределенные коэффициенты С1,С2,В1,В2
не являются независимыми. Они связаны
двумя уравнениями системы (1). Поэтому
независимых коэффициентов только два.
Общим решением системы (1) называется решение:

 из
которого путем выбора конкретных
значений производных независимых
постоянных С1, С2 может быть получено
любое решение этой системы, которое
называется частным решением.
из
которого путем выбора конкретных
значений производных независимых
постоянных С1, С2 может быть получено
любое решение этой системы, которое
называется частным решением.
