
- •1. Классические принципы управления.
- •2. Основные определения теории автоматического регулирования.
- •3. Классификация систем автоматического регулирования.
- •1) По характеру изменения управляющего воздействия:
- •5. Составление и линеаризация дифференциальных уравнений в теории автоматического регулирования.
- •6. Понятие передаточной функции и частотных характеристик системы автоматического регулирования.
- •7. Классификация типовых звеньев системы автоматического регулирования.
- •8. Передаточные функции и частотные характеристики типовых звеньев системы автоматического регулирования.
- •9. Понятие устойчивости системы по Ляпунову.
- •10. Общие условия устойчивости линейных систем.
- •11. Критерий устойчивости Гурвица.
- •12. Критерий устойчивости Михайлова.
- •13. Критерий устойчивости Найквиста.
- •14. Понятие точности систем автоматического регулирования.
- •15. Качество переходного процесса.
- •16. Частотные методы оценки качества переходного процесса.
- •17. Корневые методы оценки качества переходного процесса.
- •18. Интегральные методы оценки качества переходного процесса.
- •19. Классификация корректирующих устройств для линейных систем: последовательные и параллельные корректирующие устройства.
- •21. Постановка задачи синтеза корректирующих устройств.
- •22. Основные понятия и типы дискретных систем.
- •23. Сущность и свойства импульсных систем.
- •24. Сущность и свойства цифровых систем.
- •25. Нелинейные системы автоматического регулирования. Классификация нелинейностей.
- •26. Понятие фазового пространства и фазовой плоскости.
- •27. Общие представления о процессе развития систем управления.
- •28.Общее информационное представление системы управления.
- •29. Информационные структуры систем управления.
- •30. Развитие систем управления в виде индивидуальной адаптации.
- •31. Классификация адаптивных систем.
- •32.Развитие систем управления в виде групповой адаптации.
- •33. Структуры и свойства систем группового поведения.
15. Качество переходного процесса.
t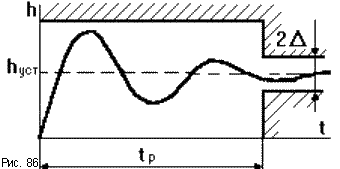 п-длительность
пп,плавность кривой-огранич.по скорости
и ускорению,Ϭ-перерегулирование,опр-ет
склонность сист.к колебаниям,запас
устойчивости.Длит.пп ограничив.моментом
когда отклонение колебаний Δ=|x-xуст|≤5%.
Счит.что запас устойчивости явл
достаточным if
перерегулирование Ϭ=(хmax-
xуст)/
xуст*100%<30%
При Ϭ=0 процесс наз-я монотонным. Сущ 3
осн. вида приближ.оценок качества
пп:-частотные-корневые-интегральные.
п-длительность
пп,плавность кривой-огранич.по скорости
и ускорению,Ϭ-перерегулирование,опр-ет
склонность сист.к колебаниям,запас
устойчивости.Длит.пп ограничив.моментом
когда отклонение колебаний Δ=|x-xуст|≤5%.
Счит.что запас устойчивости явл
достаточным if
перерегулирование Ϭ=(хmax-
xуст)/
xуст*100%<30%
При Ϭ=0 процесс наз-я монотонным. Сущ 3
осн. вида приближ.оценок качества
пп:-частотные-корневые-интегральные.
16. Частотные методы оценки качества переходного процесса.
Частотные
методы основаны на привычном для
инженеров графическом изображении
динамических характеристик, которые
можно снять экспериментально, поэтому
они находят широкое применение. В
частности зная АФЧХ разомкнутой
САУ Wp(j![]() ),
можно построить АФЧХ замкнутой САУ
),
можно построить АФЧХ замкнутой САУ
Wз(j
)
= ![]() =
Pз(
)
+ jQз(
),
=
Pз(
)
+ jQз(
),
а по ней - требуемую для частотных методов вещественную ЧХ замкнутой САУ Pз( ). Зная ВЧХ замкнутой САУ, можно приближенно построить переходную характеристи САУh(t), которую снять экспериментально очень трудно, и по ней определить показатели качества управления.
Теоретическое обоснование этого в том, что любую функцию, в том числе и единичную ступенчатую, можно разложить в ряд Фурье:
1(t)
= A0 + ![]() Ak1cos(k
t)
+ Ak2sin(k
t)].
Ak1cos(k
t)
+ Ak2sin(k
t)].
Так
как замкнутая САУ линейна, то при подаче
на вход суммы сигналов с выхода снимается
сигнал, равный сумме реакций на каждый
из входных сигналов. Входному сигналу
ui(wi,t) на выходе будет соответствовать
составляющая выходного сигнала yi(
i,t)
= W(j
i)![]() ui(
i,t),
тогда
ui(
i,t),
тогда
h(t)
= ![]() =
A0W(0)
+
=
A0W(0)
+ ![]() (jkw)
[Ak1cos(kwt)
+ Ak2sin(kwt)].
(jkw)
[Ak1cos(kwt)
+ Ak2sin(kwt)].
Преобразование этого выражения приводит к двум равнозначным формулам определения h(t) через составляющие ВЧХ
![]() ;
; ![]() ,
,
где P( ) и Q( ) - вещественная и мнимая части АФЧХ замкнутой САУ. Предпочтение обычно оказывают первой формуле, хотя с одинаковым успехом можно использовать и вторую.
Точно вычислить эти интегралы можно только с помощью ЭВМ, но в практике нашел широкое применение приближенный способ построения переходной характеристики на основе линейной аппроксимации ВЧХ замкнутой САУ, который называется метод трапеций. Прежде, чем рассматривать этот метод, рассмотрим без доказательства основные соотношения между ВЧХ замкнутой САУ и ее переходной характеристикой.
17. Корневые методы оценки качества переходного процесса.
Основаны на анализе вида корней характеристического уравнения, определяющих характер переходного процесса. Для оценки быстродействия системы используется понятие степень устойчивости. Под степенью устойчивости (Y) понимается абсолютное значение вещественной части ближайшего к мнимой оси корня.
Возможны два случая:
а) Ближайшим к оси является вещественный корень
б) Ближе всего к мнимой оси располагается пара комплексно сопряженных корней.
Корни характеристического уравнения, расположенные ближе всего к оси мнимых, т. е. имеющие по модулю вещественная часть, дают в переходном процессе члены, которые затухают наиболее медленно и определяют таким образом момент окончания переходного процесса.
Склонность
системы к колебаниям будет наблюдаться,
если в решении характеристического
уравнения будут присутствовать
комплексные корни стандартного вида
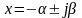 .
Эта склонность характеризуется величиной,
называемой колебательностью переходного
процесса
.
Эта склонность характеризуется величиной,
называемой колебательностью переходного
процесса
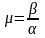 .
Чем больше по модулю μ,
тем слабее будут затухания колебаний
переходного процесса.
.
Чем больше по модулю μ,
тем слабее будут затухания колебаний
переходного процесса.
