12. Критерий устойчивости Михайлова.

Устойчивость САР является одним из важнейших условий работоспособности этой системы.

Если под влиянием возмущения система отклоняется от состояния равновесия или заданного закона движения, а после прекращения действия внешнего возмущения снова возвращается к исходному состоянию, то движение в системе является устойчивым, сходящимся к исходному состоянию. Т. о. под устойчивостью линейной системы понимают свойство затухания переходного процесса с течением времени.

Неустойчивая система непрерывно удаляется от равновесного состояния или совершает вокруг него колебания с возрастающей амплитудой.

Система устойчива «в малом», если определен факт наличия устойчивости, но не определены его границы.

Система устойчива «в большом», когда определен факт наличия устойчивости, выявлены границы устойчивости и то, что реальные отклонения не выходят за эти границы.

Принцип устойчивости Михайлова – принцип аргумента.

Пусть характеристическое уравнение линейной системы имеет вид: . Пусть . Тогда осуществляется переход на комплексную плоскость и к частотной характеристике:

Пусть ω изменяется от 0 до ∞. Тогда координаты комплексной плоскости (X, Y) образуют кривую – годограф Михайлова – в ходе изменения ω.

Для устойчивости линейной системы n-ого порядка необходимо и достаточно, чтобы изменение аргумента функции 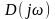при изменении ω от 0 до ∞ имели следующий вид: . Иначе говоря, необходимо, чтобы кривая Михайлова последовательно проходила n квадрантов (четвертей) комплексной плоскости против часовой стрелки.

Достоинства: этот критерий удобен наглядностью. Так, если кривая проходит вблизи начала координат, то САУ находится вблизи границы устойчивости и наоборот. Такой критерий удобно использовать, если известно уравнение замкнутой САУ.

13. Критерий устойчивости Найквиста.

Устойчивость САР является одним из важнейших условий работоспособности этой системы.

Если под влиянием возмущения система отклоняется от состояния равновесия или заданного закона движения, а после прекращения действия внешнего возмущения снова возвращается к исходному состоянию, то движение в системе является устойчивым, сходящимся к исходному состоянию. Т. о. под устойчивостью линейной системы понимают свойство затухания переходного процесса с течением времени.

Неустойчивая система непрерывно удаляется от равновесного состояния или совершает вокруг него колебания с возрастающей амплитудой.

Система устойчива «в малом», если определен факт наличия устойчивости, но не определены его границы.

Система устойчива «в большом», когда определен факт наличия устойчивости, выявлены границы устойчивости и то, что реальные отклонения не выходят за эти границы.

Критерий устойчивости Найквиста – частотный критерий. Позволяет по виду АФХ разомкнутой системы судить об устойчивости замкнутой.

14. Понятие точности систем автоматического регулирования.

Точность-степень близости к реальному сост.сист.,к треб.сост.в установл.режиме. Опр-я через простые звенья: а)сигнал с постоянным воздействием g(t)=const-g₀ ε_ст= g₀/1+k –статическая ошибка,k-коэфф.усиления б)сигнал измен.с постоянной скоростью g(t)=g₀+g₁(t) в этом случае ε так же будет изменятся с пост.скоростью ε_ск= g₁/k-скоростная ошибка. Для уменьш.величины ошибки ε_ст;ск необх.добиваться достаточно больш.знач.коэфф.k(иногда наз-ют добротность сист.) в)гармонич.воздействие Установивш.ε опр-я частотными хар-ми замкн.сист.по амплитуде и по фазе.Как правило A(w)->0, w->͚ в рез-те получается ограниченный диапазон частот в кот.ошибка по амплитуде ΔA=1-A(0) не превышает допустимого значения.Этот диапазон частот опр-ет полосу пропускания сист.Э тот показ.хар-ий ограничение возможн.сист.в воспроизвед.быстродейств.сигналов,так наз-я инерциальность.